العنوان الأصلي: توقيعات المحول وتطبيقها على المقايضة الذرية عبر السلاسل

الرابط الأصلي: https:/ /blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

المؤلف: Mutourend, lynndell

1. مقدمة

مع التطور السريع لخطة توسيع الطبقة الثانية من Bitcoin، زاد تكرار عمليات نقل الأصول عبر السلسلة بين Bitcoin وشبكتها المقابلة من الطبقة الثانية بشكل ملحوظ . ويعود هذا الاتجاه إلى قابلية التوسع العالية، وانخفاض رسوم المعاملات، والإنتاجية العالية التي توفرها تقنيات الطبقة الثانية مثل Bitlayer. تعمل هذه التطورات على تسهيل معاملات أكثر كفاءة واقتصادية، وبالتالي تعزيز اعتماد وتكامل Bitcoin على نطاق أوسع عبر مجموعة متنوعة من التطبيقات. ونتيجة لذلك، أصبحت قابلية التشغيل البيني بين شبكات البيتكوين وشبكات الطبقة الثانية مكونًا رئيسيًا في النظام البيئي للعملات المشفرة، مما يؤدي إلى تحفيز الابتكار وتزويد المستخدمين بأدوات مالية أكثر تنوعًا وقوة.

كما هو موضح في الجدول 1، هناك ثلاثة حلول نموذجية للمعاملات عبر السلسلة بين Bitcoin والطبقة الثانية، وهي المعاملات المركزية عبر السلسلة وBitVM عبر السلسلة الجسر والمقايضات الذرية عبر السلسلة. تختلف هذه التقنيات الثلاث من حيث افتراضات الثقة والأمان والراحة وحدود المعاملات وما إلى ذلك، ويمكن أن تلبي احتياجات التطبيقات المختلفة.

الجدول 1. مقارنة تقنيات المعاملات عبر السلسلة

معاملة مركزية عبر السلسلة: المستخدمون أولاً بتات التحويل إذا تم دفع العملة إلى مؤسسة مركزية (مثل طرف مشروع أو بورصة)، فستدفع المؤسسة المركزية القيمة المكافئة للأصول إلى العنوان المحدد من قبل المستخدم على شبكة الطبقة الثانية، وبالتالي إكمال عملية النقل المتقاطعة. نقل أصول السلسلة. وتتمثل ميزة هذه التكنولوجيا في أنها سريعة وأن عملية المطابقة سهلة نسبيًا لأن المؤسسة المركزية يمكنها تأكيد المعاملة ومعالجتها بسرعة. ومع ذلك، فإن أمان هذه الطريقة يعتمد كليًا على موثوقية ومصداقية المؤسسة المركزية. إذا واجهت المؤسسة المركزية أعطالًا فنية أو هجمات ضارة أو حالات افتراضية، فستواجه أموال المستخدمين مخاطر أعلى. بالإضافة إلى ذلك، قد تؤدي المعاملات المركزية عبر السلسلة أيضًا إلى تسريب خصوصية المستخدم، ويحتاج المستخدمون إلى التفكير بعناية عند اختيار هذه الطريقة. لذلك، على الرغم من أن الراحة والفعالية توفران للمستخدمين راحة كبيرة، إلا أن الأمان والثقة يمثلان التحديات الرئيسية التي تواجه المعاملات المركزية عبر السلسلة.

جسر BitVM عبر السلسلة: هذه التكنولوجيا معقدة نسبيًا. أولاً، في مرحلة الربط، يدفع المستخدمون عملة البيتكوين إلى عنوان متعدد التوقيع يتحكم فيه تحالف BitVM لقفل عملة البيتكوين. يتم سك عدد مماثل من الرموز المميزة في الطبقة الثانية، ويتم استخدام الرموز المميزة لتنفيذ معاملات وتطبيقات الطبقة الثانية. عندما يقوم المستخدم بتدمير رمز الطبقة الثانية، سيقوم المشغل بالدفع مقدمًا. بعد ذلك، يقوم المشغل بتعويض العدد المقابل من عملات البيتكوين في مجموعة التوقيعات المتعددة التي يتحكم فيها تحالف BitVM. من أجل منع المشغلين من ارتكاب الشر، تعتمد عملية السداد آلية تحدي متفائلة، أي أنه يمكن لأي طرف ثالث تحدي سلوكيات السداد الضارة وإحباط السلوكيات الشريرة. تقدم هذه التكنولوجيا آلية تحدي متفائلة، وبالتالي فإن التكنولوجيا معقدة نسبيا. بالإضافة إلى ذلك، تتضمن آلية التحدي المتفائل عددًا كبيرًا من معاملات التحدي والاستجابة، مع ارتفاع رسوم المعاملات. لذلك، فإن جسر BitVM عبر السلسلة مناسب فقط للمعاملات الكبيرة جدًا، على غرار الإصدار الإضافي لـ U، وبالتالي يتم استخدامه بشكل أقل تكرارًا.

المبادلة الذرية عبر السلسلة: المبادلة الذرية هي عقد ينفذ معاملات العملة المشفرة اللامركزية. وفي هذا السياق، تعني كلمة "ذري" أن التغيير في ملكية أحد الأصول يعني في الواقع تغييرًا في ملكية أصل آخر. تم اقتراح هذا المفهوم لأول مرة بواسطة TierNolan في منتدى Bitcointalk في عام 2013. لمدة أربع سنوات، ظلت المقايضة الذرية في نطاق النظرية. حتى عام 2017، أصبح ديكريد ولايتكوين أول أنظمة بلوكتشين تنجح في إكمال عمليات المبادلة الذرية. يجب أن تتضمن المبادلات الذرية طرفين، ولا يمكن لأي طرف ثالث أن يقاطع عملية المبادلة أو يتدخل فيها. وهذا يعني أن التكنولوجيا لا مركزية، وغير خاضعة للرقابة، وتتمتع بحماية جيدة للخصوصية، ويمكنها تحقيق معاملات عالية التردد عبر السلسلة، وبالتالي يتم استخدامها على نطاق واسع في التبادلات اللامركزية. حاليًا، تتطلب المبادلة الذرية عبر السلسلة 4 معاملات، وتحاول بعض الحلول ضغط عدد المعاملات إلى 2، ولكن هذا سيزيد من المتطلبات عبر الإنترنت في الوقت الفعلي لكلا طرفي البورصة. أخيرًا، تتضمن تقنية المبادلة الذرية عبر السلسلة بشكل أساسي أقفال وقت التجزئة وتوقيعات المحول.

المبادلة الذرية عبر السلسلة استنادًا إلى Hash Time Lock (HTLC): أول مشروع ينفذ بنجاح المبادلة الذرية عبر السلسلة هو Decred، والذي يستخدم "قفل التجزئة" "" و"قفل الوقت" يحققان التبادل الذري الذي اقترحه TierNolan بمساعدة البرامج النصية الموجودة على السلسلة (أو العقود الذكية). يسمح HTLC لمستخدمين بإجراء معاملات عملة مشفرة لفترة زمنية محدودة، أي أنه يجب على المستلم تقديم إثبات تشفير ("سري") للعقد خلال فترة زمنية محددة (يتم تحديدها بواسطة رقم الكتلة أو ارتفاع الكتلة)، وإلا سيتم إرجاع الأموال إلى المرسل بواسطة. إذا أكد المستلم الدفع، تكون المعاملة ناجحة. لذلك، يجب أن يكون لكل من البلوكشين المشاركين وظيفتي "قفل التجزئة" و"قفل الوقت".

على الرغم من أن المبادلة الذرية HTLC تعد إنجازًا كبيرًا في مجال تكنولوجيا التبادل اللامركزي، إلا أن هناك المشكلات التالية. يتم تنفيذ معاملات المبادلة الذرية هذه والبيانات المتعلقة بها على السلسلة، مما يؤدي إلى تسرب خصوصية المستخدم. بمعنى آخر، في كل مرة يكون هناك تبادل، ستظهر نفس التجزئة على كلا البلوكشين، مفصولة ببضع كتل فقط. وهذا يعني أنه يمكن للمراقبين ربط العملات المشاركة في البورصة، أي العثور على نفس قيمة التجزئة في الكتل القريبة من بعضها البعض (TimeStamp-wise). عند تتبع العملة عبر السلاسل، يكون من السهل تحديد المصدر. على الرغم من أن هذا التحليل لا يكشف عن أي بيانات تعريفية ذات صلة، إلا أنه يمكن لأطراف ثالثة بسهولة استنتاج هويات الجهات الفاعلة المعنية.

المبادلة الذرية عبر السلسلة استنادًا إلى توقيع المحول: يُطلق على التبادل الثاني المقدم من BasicSwap اسم المبادلة الذرية "توقيع المحول"، استنادًا إلى الورقة A الخاصة بمطور Monero Joël Gugger بعنوان "Bitcoin – Monero Cross-chain Atomic Swap}" نُشر في عام 2020. يمكن القول أن هذه الورقة هي تطبيق لورقة Lloyd Fournier لعام 2019 الخاصة بالتوقيعات المشفرة التي يمكن التحقق منها لمرة واحدة، A.K.A. توقيع المحول هو توقيع إضافي يتم دمجه مع التوقيع الأولي للكشف عن البيانات السرية، مما يمكّن كلا الطرفين من الكشف عن قطعتي البيانات لبعضهما البعض في وقت واحد، وهو مكون رئيسي في البروتوكول بدون نص الذي يجعل أزواج المبادلة الذرية لمونيرو ممكنة.

مقارنة بالمبادلة الذرية HTLC، تتمتع المبادلة الذرية المستندة إلى توقيع المحول بثلاث مزايا: أولاً، يحل نظام تبادل توقيع المحول محل تبادل "التجزئة السرية" المعتمد على- البرامج النصية المتسلسلة، بما في ذلك أقفال الوقت وأقفال التجزئة. بمعنى آخر، ليس للتجزئة السرية والسرية في تبادل HTLC أي مراسلات مباشرة في تبادل توقيع المحول. ولذلك، يطلق عليها "النصوص البرمجية بدون نصوص برمجية" في مجتمع أبحاث البيتكوين. بالإضافة إلى ذلك، نظرًا لعدم وجود مثل هذه البرامج النصية، يتم تقليل المساحة المشغولة على السلسلة، مما يجعل المقايضات الذرية المستندة إلى توقيعات المحول أكثر خفة الوزن وأرخص. أخيرًا، يتطلب HTLC من كل سلسلة استخدام نفس قيمة التجزئة، ولا يمكن ربط المعاملات المتضمنة في المقايضات الذرية الموقعة بواسطة المحول، مما يحقق حماية الخصوصية.

تقدم هذه المقالة أولاً توقيع محول Schnorr/ECDSA ومبدأ التبادل الذري عبر السلسلة. بعد ذلك، قم بتحليل مشكلات أمان الأرقام العشوائية الموجودة في توقيع المحول ومشكلات عدم تجانس النظام وعدم تجانس الخوارزمية في السيناريوهات عبر السلسلة، وتقديم الحلول. وأخيرًا، يتم توسيع توقيع المحول وتطبيقه لتحقيق حفظ الأصول الرقمية غير التفاعلية.

2. توقيع المحول والتبادل الذري عبر السلسلة

2.1 توقيع محول Schnorr والتبادل الذري تبادل

< /h2>

p>

2.2 توقيع محول ECDSA والمبادلة الذرية

2.2.1 إثبات المعرفة الصفرية zk{v | Ṽ = vᐧ G, V = v ᐧ Y}

3. المشكلات الأمنية والحلول

3.1 مشاكل وحلول الأرقام العشوائية

3.1.1 مشكلة تسرب الأرقام العشوائية

محول Schnorr/ECDSA جميع التوقيعات المسبقة الموقعة تلتزم برقم عشوائي $r$ ş = r ᐧ G. بالإضافة إلى ذلك، يعد إثبات المعرفة الصفرية بالرقم العشوائي $v$ الذي $Ṽ=v ᐧ G,V=v ᐧ Y$. إذا تم تسريب الرقم العشوائي، فسيتم تسريب المفتاح الخاص.

على وجه التحديد، في بروتوكول شنور، إذا تم تسريب الرقم العشوائي $r$، فيمكن تحديده وفقًا للمعادلة

$ŝ  = r + c x.$

احسب المفتاح الخاص $x$.

وبالمثل، في بروتوكول ECDSA، إذا تسرب الرقم العشوائي $r$، فيمكن حسابه وفقًا للمعادلة

$ŝ = r^{-1}(hash(m)+R_x x).$

احسب المفتاح الخاص لـ احصل على $x$.

أخيرًا، في بروتوكول إثبات المعرفة الصفرية، إذا تم تسريب الرقم العشوائي $v$، فيمكن تحديده وفقًا للمعادلة

احسب الرقم العشوائي $r$، ثم أبعد احسب بناءً على الرقم العشوائي $r$ واستخرج المفتاح الخاص $x$. ولذلك، يجب حذف الأرقام العشوائية مباشرة بعد الاستخدام.

3.1.2 مشكلة إعادة استخدام الأرقام العشوائية

بالنسبة لأي معاملتين عبر السلسلة، إذا إذا كان بروتوكول توقيع المحول يستخدم نفس الرقم العشوائي، فسيتم تسريب المفتاح الخاص. على وجه التحديد، في بروتوكول شنور، إذا تم استخدام نفس الرقم العشوائي $r$، فإن $r$ و$x$ فقط غير معروفين في نظام المعادلات التالي

$ŝ_1 =r + c_1 x, $

 $ ŝ_2 = r + c_2 x $

وبالتالي يمكن حل نظام المعادلات للحصول على المفتاح الخاص $x$.

وبالمثل، في بروتوكول توقيع محول ECDSA، إذا تم استخدام نفس الرقم العشوائي $r$، فقط $r$ و$x$ في النظام التالي من المعادلات غير معروفة

$ ŝ_1 = r^{-1}(hash(m_1)+R_x x),$

$ ŝ_2 = r^{-1}(hash(m_2)+R_x x).$

وبالتالي فإن نظام المعادلات يمكن حلها بالحصول على المفتاح الخاص $x$.

أخيرًا، في بروتوكول إثبات المعرفة الصفرية، إذا تم استخدام نفس الرقم العشوائي $v$، فقط $v$ و$r$ في النظام التالي من المعادلات غير معروفة

$z_1 = v+c_1 r, $

 $ z_2 = v+c_2 r $

وبالتالي يمكن حل نظام المعادلات للحصول على الرقم العشوائي $r$، ويمكن حل نظام المعادلات تم حلها أيضًا للحصول على المفتاح الخاص $x$.

بالقياس، إذا استخدم مستخدمون مختلفون نفس الرقم العشوائي، فسيتم أيضًا تسريب المفتاح الخاص. بمعنى آخر، يمكن لمستخدمين يستخدمان نفس الرقم العشوائي حل نظام المعادلات والحصول على المفتاح الخاص لكل منهما. لذلك، يجب استخدام RFC 6979 لمعالجة مشكلة إعادة استخدام الأرقام العشوائية.

3.1.3 الحل: RFC 6979

يحدد RFC 6979 طريقة تستخدم DSA الطريقة إنشاء التوقيعات الرقمية الحتمية باستخدام ECDSA يحل المشكلات الأمنية المتعلقة بإنشاء قيم عشوائية k. تعتمد توقيعات DSA وECDSA التقليدية على رقم عشوائي k يتم إنشاؤه عشوائيًا لكل عملية توقيع. إذا تم إعادة استخدام هذا الرقم العشوائي أو إنشاؤه بشكل غير صحيح، فمن الممكن أن يتعرض أمان المفتاح الخاص للخطر. يلغي RFC 6979 الحاجة إلى إنشاء أرقام عشوائية عن طريق الاشتقاق الحتمي $k$ من المفتاح الخاص والرسالة المراد توقيعها. وهذا يضمن أنه عند توقيع نفس الرسالة بنفس المفتاح الخاص، يكون التوقيع هو نفسه دائمًا، مما يعزز إمكانية التكرار والقدرة على التنبؤ. على وجه التحديد، يتم إنشاء $k$ الحتمية بواسطة HMAC. تتضمن العملية تجزئة المفتاح الخاص والرسالة والعداد باستخدام وظيفة التجزئة (مثل SHA256)،

$k = SHA256(sk, msg, counter) .$

في المعادلة أعلاه، لتبسيط التعبير، يتم حساب قيمة التجزئة فقط للمفتاح الخاص sk ورسالة الرسالة وعداد العداد العملية في RFC 6979 المزيد من حسابات التجزئة المعنية. تضمن هذه المعادلة أن تكون k فريدة لكل رسالة مع إمكانية تكرارها لنفس الإدخال وتقلل من خطر التعرض للمفتاح الخاص المرتبط بمولدات الأرقام العشوائية الضعيفة أو المخترقة. ولذلك، يوفر RFC 6979 إطارًا قويًا للتوقيعات الرقمية الحتمية باستخدام DSA وECDSA، ويحل المشكلات الأمنية المهمة المتعلقة بتوليد الأرقام العشوائية، ويعزز موثوقية التوقيعات الرقمية وإمكانية التنبؤ بها. وهذا يجعله معيارًا قيمًا للتطبيقات التي تتطلب أمانًا عاليًا وامتثالًا لمتطلبات التشغيل الصارمة. تحتوي توقيعات Schnorr/ECDSA على عيوب في الأرقام العشوائية، ويجب استخدام RFC 6979 لمنعها. ولذلك، فإن توقيعات المحول المستندة إلى Schnorr/ECDSA بها هذه المشكلات أيضًا، ويجب أيضًا استخدام مواصفات RFC 6979 لحل هذه المشكلات.

3.2 مشاكل وحلول السيناريو عبر السلسلة

3.2.1 نظام UTXO ونموذج الحساب مشاكل وحلول غير متجانسة

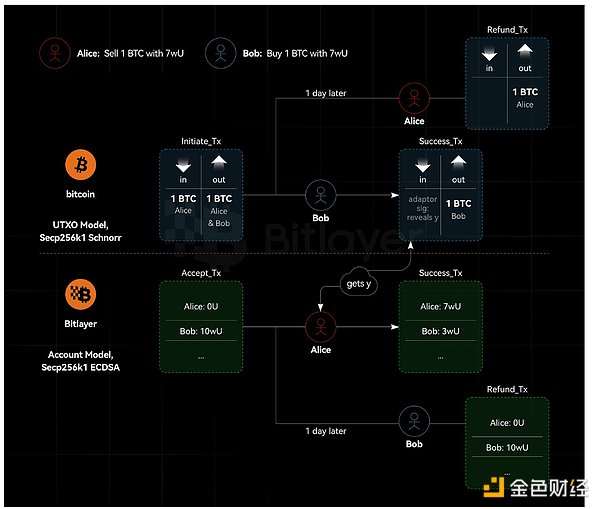
كما هو موضح في الشكل 1، تستخدم Bitcoin نموذج UTXO لتنفيذ توقيعات ECDSA الأصلية استنادًا إلى منحنى Secp256k1. Bitlayer متوافق مع EVM مع سلسلة Bitcoin L2، ويستخدم منحنى Secp256k1، ويدعم توقيعات ECDSA الأصلية. يطبق Adaptor Signature المنطق المطلوب لمقايضات BTC، في حين يتم تشغيل نظير مبادلة Bitlayer بقوة عقود Ethereum الذكية.

المقايضات الذرية عبر السلسلة المستندة إلى توقيعات المحول، أو على الأقل مخططات توقيع المحول شبه الخالية من النصوص والمصممة للعمل مع منحنى ECDSA، غير متوافقة مع Ethereum. والسبب هو أن Ethereum هو نموذج حساب، وليس نموذج UTXO. على وجه التحديد، تتطلب المقايضات الذرية المستندة إلى توقيعات المحول أن تكون معاملات الاسترداد موقعة مسبقًا. ومع ذلك، في نظام الإيثيريوم، لا يمكن التوقيع المسبق على المعاملات دون معرفة الرقم. لذلك، يمكن لأي طرف إرسال معاملة بين إكمال التوقيع المسبق وتنفيذ المعاملة - مما قد يؤدي إلى إبطال المعاملة الموقعة مسبقًا (نظرًا لأن الرقم nonce قد تم استخدامه بالفعل ولا يمكن إعادة استخدامه).

بالإضافة إلى ذلك، من منظور الخصوصية، هذا يعني أن عدم الكشف عن هوية Bitlayer Swap أفضل من HTLC (يمكن لكلا طرفي المبادلة العثور على العقد). ومع ذلك، نظرًا لأنه يتعين على أحد الأطراف الحصول على عقد عام، فإن إخفاء هوية Bitlayer Swap أقل من إخفاء هوية توقيع المحول. مع عدم وجود عقد على جانب واحد، تبدو معاملة المبادلة مثل أي معاملة أخرى. ومع ذلك، على جانب عقد EVM، من الواضح أن الصفقة تتعلق بتبادل الأصول. على الرغم من أن أحد الأطراف لديه عقد عام، فمن المستحيل إرجاعه إلى سلسلة أخرى، حتى باستخدام أدوات تحليل السلسلة المتطورة.

p>

الشكل 1. UTXO ونموذج الحساب للمبادلة الذرية للنظام غير المتجانس عبر السلسلة

طبقة البت حاليًا يدعم توقيع ECDSA الأصلي ويمكن أيضًا تنفيذ التحقق من توقيع Schnorr من خلال العقود الذكية. إذا كنت تستخدم معاملات Bitlayer الأصلية، فلا يمكنك التوقيع مسبقًا على معاملات استرداد الأموال في المقايضة الذرية؛ فستحتاج إلى استخدام معاملات عقد Bitlayer الذكية لتحقيق المقايضة الذرية. ومع ذلك، فإن هذه العملية ستضحي بالخصوصية، أي أن المعاملات المشاركة في المقايضات الذرية في نظام Bitlayer يمكن تتبعها، ولكن لا يمكن تتبع المعاملات في نظام BTC. يمكن تصميم تطبيقات Dapp مثل Tornado Cash على جانب Bitlayer لتوفير خدمات الخصوصية للمعاملات على جانب Bitlayer في مقايضات BTC وBitlayer الذرية.

3.2.2 نفس المنحنى، وخوارزمية مختلفة، وأمان توقيع المحول

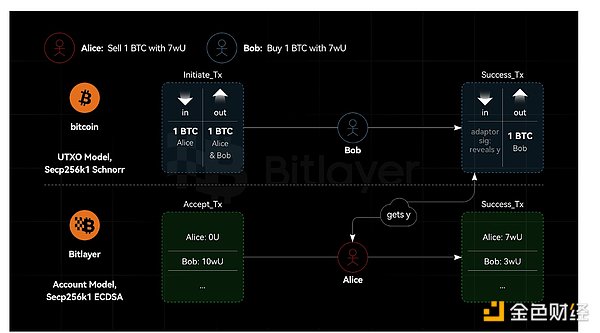
كما هو موضح في الشكل 2 كما هو موضح في الشكل، من المفترض أن كل من Bitcoin وBitlayer يستخدمان منحنى Secp256k1، لكن Bitcoin يستخدم توقيعات Schnorr ويستخدم Bitlayer ECDSA. في هذه الحالة، تكون توقيعات المحول المستندة إلى Schnorr وECDSA آمنة بشكل مؤكد. بافتراض أنه بالنظر إلى أوراكل توقيع ECDSA وSchnorr، يمكن إنشاء جهاز محاكاة S لكسر ECDSA، ثم بالنظر إلى أوراكل توقيع ECDSA فقط، يمكن إنشاء جهاز محاكاة S لكسر ECDSA. ومع ذلك، فإن ECDSA آمن. بنفس الطريقة، بافتراض أنه في ضوء أوراكل توقيع ECDSA وSchnorr، يمكن إنشاء جهاز المحاكاة S لكسر توقيع شنور، ثم بالنظر إلى أوراكل توقيع ECDSA فقط، يمكن إنشاء جهاز المحاكاة S لكسر توقيع شنور. ومع ذلك، فإن توقيعات شنور آمنة. لذلك، في سيناريو عبر السلسلة، يستخدم توقيع المحول نفس المنحنى ولكن يحتوي على خوارزميات توقيع مختلفة، وهو أمر آمن. بمعنى آخر، يسمح توقيع المحول لأحد الطرفين باستخدام ECDSA والطرف الآخر باستخدام توقيعات Schnorr.

p>

الشكل 2. نفس المنحنى، خوارزمية مختلفة، توقيع المحول

3.2.3 منحنى مختلف ، المحول التوقيع غير آمن

افترض أن Bitcoin يستخدم منحنى Secp256k1 وتوقيع ECDSA، بينما يستخدم Bitlayer منحنى ed25519 وتوقيع Schnorr. في هذه الحالة، لا يمكن استخدام توقيع المحول. نظرًا لاختلاف المنحنيات، يختلف ترتيب مجموعة المنحنيات الإهليلجية، أي أن معاملات الوحدة مختلفة. عندما يقوم بوب بتكييف $y$ مع توقيع ECDSA في نظام البيتكوين، فإنه يحسب $s:= ŝ+y$. في هذا الوقت، مساحة القيمة $y$ هي المساحة العددية لمجموعة المنحنى الإهليلجي Secp256k1. بعد ذلك، تحتاج أليس إلى استخدام $y$ لإجراء توقيع Schnorr على مجموعة المنحنى الإهليلجي ed25519. ومع ذلك، فإن العامل المساعد لمنحنى ed25519 هو 8، ومعامل الوحدة لا يساوي معامل الوحدة لمجموعة المنحنى الإهليلجي Secp256k1. لذلك، من غير الآمن استخدام $y$ لتوقيعات Schnorr على منحنى ed25519.

4. تطبيق حفظ الأصول الرقمية

يحتوي تطبيق حفظ الأصول الرقمية على ثلاثة مشاركين، وهم: المشتري أليس والبائع بوب وحفلة الضمان. يتيح استخدام توقيعات المحول إمكانية حفظ الأصول الرقمية ذات العتبة غير التفاعلية وإنشاء مجموعة فرعية من إستراتيجيات الحد الأدنى للإنفاق دون تفاعل. تتكون هذه المجموعة الفرعية من نوعين من المشاركين: المشاركون الذين يشاركون في التهيئة والمشاركين الذين لا يشاركون في التهيئة ويطلق عليهم الأخير اسم الوصي. لا يجوز لأمين الحفظ التوقيع على معاملات تعسفية ولا يرسل الأسرار إلا إلى أحد الأطراف الداعمة.

من ناحية، لا يمكن لأمين الحفظ الاختيار إلا من بين عدة معاملات تسوية ثابتة ولا يمكنه توقيع معاملات جديدة مع أحد الأطراف الأخرى. ولذلك، فإن آلية الإصدار السري هذه تجعل استضافة العتبة غير التفاعلية أقل مرونة من توقيعات عتبة شنور. من ناحية أخرى، يمكن إعداد سياسة إنفاق 2 من 3 باستخدام توقيعات عتبة شنور. ومع ذلك، يتطلب بروتوكول توقيع عتبة شنور ثلاثة أطراف لتشغيل بروتوكول توليد المفاتيح اللامركزي. لذلك، تتمتع بروتوكولات ضمان الأصول المستندة إلى توقيعات المحول بميزة كونها غير تفاعلية.

4.1 استضافة الأصول غير التفاعلية بناءً على توقيع المحول

الشكل 3. عدم الخطية بناءً على توقيع المحول ضمان الأصول التفاعلية

كما هو موضح في الشكل 3، يريد أليس وبوب إنشاء مخرجات معاملة 2 من 3 باستخدام إستراتيجية خفية تحتوي على ضمان مربع. اعتمادًا على الشرط $c$، يمكن لـ Alice أو Bob إنفاق مخرجات المعاملة. إذا كان هناك نزاع بين Alice وBob، فإن الوصي (المفتاح العام هو $E$، والمفتاح الخاص هو $e$) هو الذي يقرر ما إذا كان Alice أو Bob سيحصلان على الأصل.

1. إنشاء معاملة تمويل غير موقعة لإرسال BTC إلى شخص ما بين Alice وBob 2-of- 2 مخرج MuSig.

2. تختار أليس قيمة عشوائية $t_A$، وتقوم بتعيين Schnorr للتوقيع المسبق$ لمحول المعاملة إلى $t_A ᐧ  يتم إرسال G$ (\hat{R}_A,\hat{s}_A)$ إلى Bob. تهدف هذه المعاملة إلى إرسال مخرجات التمويل إلى Bob. ترسل أليس أيضًا نصًا مشفرًا إلى بوب، والذي يحتوي على \textbf{تشفير قابل للتحقق}$ للسر $t_A$ وتقوم بضبط مفتاح الضمان العام $E$ إلى $E_c = E + hash(E, c)G$ C = Enc (E_c، t_A)$. خلال هذه العملية، بعد أن يتلقى بوب التوقيع المسبق من أليس، يضيف توقيعه الخاص، والذي لا يفي بـ 2 من 2 MuSig وبالتالي لا يمكنه إنفاق مخرجات التمويل. لا يمكن إنفاق مخرجات التمويل إلا إذا كان بوب يعرف $t_A$ (المقدم من الضمان)، أو إذا وقعت أليس أيضًا على توقيع كامل وأرسلته إلى بوب.

3. وبالمثل، يكرر بوب الخطوة (2) استنادًا إلى سر المحول الخاص به $t_B$. الصفقة التي وقعها بوب في هذا الوقت هي إرسال مخرجات التمويل إلى أليس.

4. يتحقق كل من أليس وبوب من صحة النص المشفر المستلم ويؤكدان أن النص المشفر هو تشفير للسر $E_c$، ومن ثم قم بالتوقيع على معاملة التمويل وبثها. يلغي التشفير الذي يمكن التحقق منه الحاجة إلى مشاركة الوصي في مرحلة الإعداد ولا يتطلب عقدًا عامًا $c$.  

5. عندما يكون هناك نزاع، يمكن لأليس وبوب إرسال النص المشفر والشرط ج إلى الوصي، ويمكن للوصي أن يتم تحديد الوضع الفعلي، ويتم استخدام المفتاح الخاص المعدل $e+hash(E, c)$ لفك التشفير وإرسال $t_A/t_B$ إلى Bob/Alice.

إذا لم يكن هناك نزاع، يمكن لأليس وبوب إنفاق مخرجات MuSig 2 من 2 كما يحلو لهما. إذا كان هناك نزاع، يجوز لأي من الطرفين الاتصال بالضمان وطلب سر المحول الخاص به $t_A$ أو $t_B$. لذلك، يمكن لأحد الأطراف، بمساعدة طرف الضمان، إكمال توقيع المحول وبث معاملة التسوية.

4.2 التشفير الذي يمكن التحقق منه

نظام التشفير الكلاسيكي الذي يمكن التحقق منه استنادًا إلى اللوغاريتمات المنفصلة (التشفير العملي الذي يمكن التحقق منه و لا يمكن استخدام فك تشفير اللوغاريتمات المنفصلة) مع محولات Secp256k1، لأنها تدعم فقط التحقق من المجموعات المنظمة خصيصًا.

في الوقت الحالي، هناك طريقتان واعدتان لإجراء تشفير يمكن التحقق منه استنادًا إلى اللوغاريتمات المنفصلة Secp256k1، وهما Purify وJuggling.

تم اقتراح Purify في الأصل لإنشاء بروتوكول MuSig باستخدام رقم حتمي (DN)، مما يتطلب من كل موقّع استخدام المعرفة الصفرية لإثبات أن رقمه غير صحيح نتيجة تطبيق الوظيفة العشوائية (PRF) بشكل صحيح على المفتاح العام والرسالة. يمكن تنفيذ Purify PRF بكفاءة في الدائرة الحسابية لبروتوكول المعرفة الصفرية الخاص بـ Bulletproofs لإنشاء مخططات تشفير يمكن التحقق منها على لوغاريتمات منفصلة على Secp256k1. بمعنى آخر، استخدم zkSnark لتنفيذ تشفير يمكن التحقق منه.

تتضمن عملية التشفير أربع خطوات: (1) تقسيم اللوغاريتم المنفصل $x$ إلى أجزاء متعددة $x_k$ بطول $l$، جعل $x = \ sum _k 2^{(k-1)l} x_k$; (2) استخدم المفتاح العام $Y$ لإجراء تشفير الجمل على الجزء $x_k ᐧ  ᐧ G + r_k ᐧ 

في عملية فك التشفير، يتم فك تشفير $\{D_k, E_k\}$ للحصول على كل $x_k ᐧ  $ (نطاق القيمة هو $[0, 2^l)$).

يحتاج Purify إلى تنفيذ PRF داخل Bulletproofs، وهو أمر معقد نسبيًا، في حين أن Juggling أبسط من الناحية النظرية. بالإضافة إلى ذلك، فإن الفرق بين الاثنين في حجم الإثبات ووقت الإثبات ووقت التحقق صغير جدًا.

5. ملخص

تناقش هذه المقالة توقيع محول Schnorr/ECDSA والسلسلة المتقاطعة يتم وصف المبادئ بالتفصيل. تم إجراء تحليل متعمق لمشاكل تسرب الأرقام العشوائية والتكرار في توقيعات المحول، وتم اقتراح استخدام RFC 6979 لحل هذه المشكلات. بالإضافة إلى ذلك، فهو يحلل بالتفصيل أنه في سيناريوهات التطبيق عبر السلسلة، لا ينبغي مراعاة الفرق بين نموذج UTXO ونموذج حساب blockchain فحسب، بل يجب أيضًا مراعاة ما إذا كان توقيع المحول يدعم خوارزميات مختلفة ومنحنيات مختلفة ومشكلات أخرى. أخيرًا، يتم توسيع توقيع المحول وتطبيقه لتحقيق حفظ الأصول الرقمية غير التفاعلية، ويتم تقديم أساسيات التشفير المعنية - التشفير الذي يمكن التحقق منه - بإيجاز.

المراجع

1. Gugger J. Bitcoin-monero التبادل الذري عبر السلسلة[J]. أرشيف الطباعة الإلكترونية لعلم التشفير، 2020.

2. Fournier L. One - التوقيعات المشفرة بشكل يمكن التحقق منه والمعروفة أيضًا باسم توقيعات المحول[J].

3. https://crypto-in-action .io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

4. Pornin T. الاستخدام الحتمي للتكنولوجيا الرقمية خوارزمية التوقيع (DSA) وخوارزمية التوقيع الرقمي ذات المنحنى الإهليلجي (ECDSA)[R] 2013.

5. Komlo C, Goldberg I . FROST: توقيعات عتبة Schnorr المرنة المستديرة المُحسّنة [C] // مجالات مختارة في التشفير: المؤتمر الدولي السابع والعشرون، هاليفاكس، NS، كندا (حدث افتراضي)، 21-23 أكتوبر 2020، الأوراق المختارة المنقحة 27. Springer International Publishing، 2021 : 34-65.

6. https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/ NITE .md

7. https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps /

8. Camenisch J, Shoup V. التشفير العملي الذي يمكن التحقق منه وفك تشفير اللوغاريتمات المنفصلة[C]// المؤتمر الدولي السنوي لعلم التشفير في برلين ,. هايدلبرغ: سبرينغر برلين هايدلبرغ، 2003: 126-144.

9. Nick J, Ruffing T, Seurin Y, et al. DN: توقيعات شنور المتعددة مع علامات حتمية يمكن التحقق منها[C]// وقائع مؤتمر ACM SIGSAC لعام 2020 حول أمن الكمبيوتر والاتصالات 2020: 1717-1731.

10. Shlomovits O, Leiba O. Jugglingswap: مقايضات ذرية عبر السلسلة بدون نص[J]. arXiv preprint arXiv:2007.14423, 2020.