تتم مناقشة نموذج قانون قوة الوقت الخاص بالبيتكوين وتكامله المشترك مرة أخرى

تم إعداده بواسطة: ليو جياوليان

مطبعة جياوليان:تمت ترجمة هذا المقال من مقالة "نموذج قانون قوة الوقت في البيتكوين وتحليله" بقلم هارولد كريستوفر برجر وبيتر فيجن " تمت إعادة النظر في قانون القوة والتكامل المشترك القائم على الوقت في Bitcoin، 2024.1.31" وهو أمر نظري للغاية ومناسب للقراء الذين لديهم أساس إحصائي معين. من أجل تسهيل فهم القراء الذين ليس لديهم معرفة أساسية كافية، ستقدم سلسلة التدريس أولاً بعض التوضيحات البسيطة.

أما بالنسبة لما يسمى بنموذج قانون قوة الوقت، فقد كتب جياو ليان العديد من المقالات لتقديمه في السنوات القليلة الماضية.

لطالما دعا PlanB، وهو محلل مجهول معروف نسبيًا في الصناعة، إلى استخدام صلابة S2F لنمذجة الأسعار. وهذا ما يسمى بنموذج S2F. لكن للأسف: نموذج S2F خاطئ. ولكن يرجى ملاحظة أن هذا لا يعني أن مؤشر S2F لا معنى له، بل يعني فقط أن العلاقة بين التغيرات في صلابة S2F والسعر ليست "جذرية" كما يصور PlanB.

يوضح الشكل التالي بوضوح العلاقة النسبية بين نموذج قانون القوة ونموذج S2F:

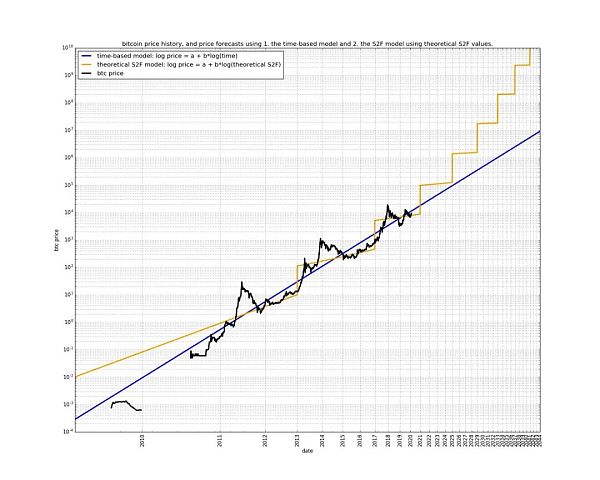
من الواضح أن نموذج S2F يعتقد أن المرور الخطي للوقت يمكن أن يدفع النمو الأسي للأسعار، في حين يعتقد نموذج قانون الطاقة أن المرور الأسي للوقت يمكن أن يدفع النمو الأسي للأسعار.

تفضل سلسلة التدريس استخدام صلابة S2F لتصور "تغير الطور" الناتج عن انخفاض الإنتاج إلى النصف، ولكنها تستخدم نموذج قانون القوة لتحويل Bitcoin إلى مساحة سجل للانحدار الخطي . تشبه أناقة نموذج قانون الطاقة بشكل خاص آلة ناقل الدعم (SVM)، لذا فهي مناسبة جدًا بالنسبة لي.

في ما يلي المقالة التي أعدها H. Burger & P. ​​Vijn. استمتع!

* * *

مقدمة

قانون القوة المعتمد على الوقت في عملة البيتكوين، المقترح في البداية بقلم جيوفاني سانتوستاسي في عام 2014 وأعيد صياغته بواسطتنا في عام 2019 (كممر أو نموذج ثلاثي المعلمات)، فهو يصف العلاقة بين سعر البيتكوين والوقت. على وجه التحديد، يصف النموذج العلاقة الخطية بين لوغاريتم عدد الأيام منذ كتلة نشأة البيتكوين ولوغاريتم سعر البيتكوين بالدولار الأمريكي.

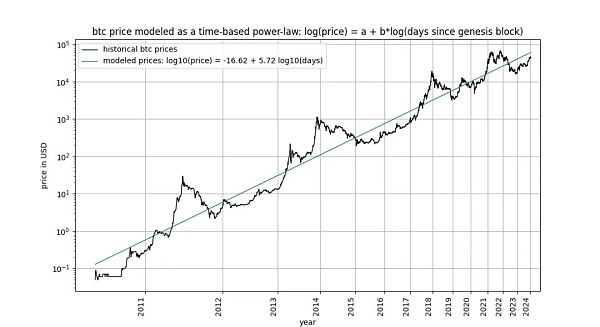
جذبت العارضة مصممين من بينهم مارسيل برجر وتيم ستولت ونيك إمبلو وقد انتقد العديد من النقاد مقالات مكتوبة "تدحض" النموذج. في هذه المقالة، سنكشف عن إحدى الحجج الرئيسية في كل من هذه الانتقادات الثلاثة: الادعاء بعدم وجود تكامل مشترك بين الوقت والسعر، بحجة أن النموذج "غير صالح" ويشير ببساطة إلى علاقة زائفة.

هل هذا هو الحال بالفعل؟

في هذه المقالة، سنلقي نظرة فاحصة على هذه المشكلة. وهذا يقودنا إلى استنتاج مفاده أن التكامل المشترك، بالمعنى الدقيق للكلمة، لا يمكن أن يوجد في النماذج المعتمدة على الوقت، بما في ذلك نماذجنا الخاصة. ومع ذلك، لا يمكن إنكار أن إحدى الخصائص الإحصائية اللازمة للتكامل المشترك موجودة في نماذج قانون القوة المستندة إلى الزمن. ولذلك، نستنتج أن نموذج قانون القوة المبني على الزمن متكامل بالمعنى الضيق، وأن انتقاداتنا في غير محلها، وأن النموذج صحيح تماما. لقد أظهرنا أن هذا الاستنتاج ينطبق بشكل متساوٍ على نموذج نسبة المخزون إلى الصندوق (S2F) والنمو الهائل الملحوظ في أسعار مؤشرات سوق الأسهم على المدى الطويل.

مقدمة للمفاهيم

ما هو التكامل المشترك

هل ضللت طريقك؟ ربما لم تكن على دراية بمصطلح "التكامل المشترك"؟ لا تقلق: يدعي جوديا بيرل، الخبير في الاستدلالات السببية والعلاقات غير الزائفة ومؤلف كتاب لماذا، أنه لا يعرف شيئًا عن هذا الموضوع. سنسعى جاهدين لتوضيح المصطلحات ذات الصلة المطروحة بشكل كامل.

إن الجدل الدائر حول التكامل المشترك في المناقشات المتعلقة بالبيتكوين على تويتر مثير جدًا ورائع للغاية. العديد من أتباع نسب المخزون إلى الزيادة وقوانين القوة في حيرة من أمرهم. يمكن للقراء المهتمين رؤية ذلك بأنفسهم من خلال البحث عن "ما هو التكامل المشترك". مع مرور الوقت، يبدو أن بعض المساهمين قد أتقنوا فهمهم وصقلوه، في حين ظل آخرون مشوشين، أو غيروا جانبهم، أو أصبحوا مشوشين. الآن فقط ننتبه لهذا الموضوع.

بعض المعلومات الأساسية أولاً

تتضمن العمليات العشوائية متغيرات عشوائية. لم يتم تحديد قيمة المتغير العشوائي مسبقًا. في المقابل، يمكن التنبؤ بالعملية الحتمية بدقة مقدمًا، فكل جانب منها معروف مسبقًا. أسعار سوق الأوراق المالية وغيرها هي متغيرات عشوائية لأننا لا نستطيع التنبؤ بسعر الأصل مقدما. ولذلك، فإننا نتعامل مع السلاسل الزمنية مثل أسعار الأسهم أو البيتكوين كملاحظات لمتغيرات عشوائية.

بدلاً من ذلك، يتبع مرور الوقت نمطًا حتميًا. كل ثانية تمر دون أي شك. ولذلك، فإن المدة بعد وقوع الحدث هي متغير حتمي.

ثبات الإشارة

قبل دراسة التكامل المشترك، دعونا أولاً نلقي نظرة على المفهوم الأساسي للتكامل المشترك: ثابت:

< p>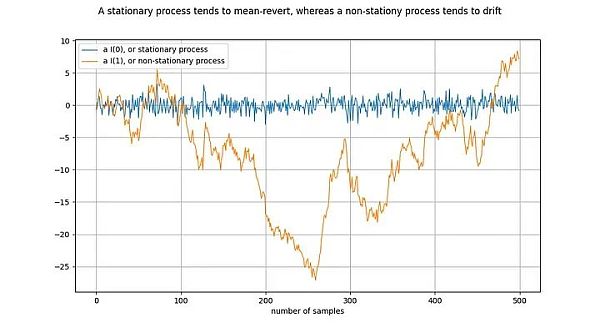

شكل توضيحي: قم بتفريق الخط البرتقالي مرة واحدة للحصول على الخط الأزرق. افرق السلسلة الزمنية I(1) مرة واحدة للحصول على السلسلة الزمنية I(0).

العملية الثابتة (العملية الثابتة) هي عملية عشوائية، بشكل عام، لها نفس الخصائص على مدار فترة زمنية. على سبيل المثال، بالنسبة لعملية ثابتة، يتم تحديد متوسطها وتباينها وثباتهما. مرادف لسلسلة زمنية ثابتة هو أنا (0). يجب ألا "تنجرف" السلاسل الزمنية المشتقة من العمليات الثابتة، بل يجب أن تميل إلى القيمة المتوسطة، والتي عادة ما تكون صفر.

مثال على عملية غير ثابتة هو السير العشوائي، مثل الحركة البراونية أو انتشار الجسيمات في الفيزياء: كل قيمة جديدة في السير العشوائي تعتمد على القيمة السابقة بالإضافة إلى رقم عشوائي. تتغير خصائص العملية غير الثابتة، مثل المتوسط ​​والتباين، بمرور الوقت أو لم يتم تعريفها. العمليات غير الثابتة هي I(1) أو أعلى، ولكن عادةً ما تكون I(1). السلاسل الزمنية الناشئة عن العمليات غير الثابتة سوف "تنجرف" بمرور الوقت، أي تميل إلى الانحراف عن أي قيمة ثابتة.

يشير الترميز I(1) إلى عدد المرات التي تحتاج فيها السلسلة الزمنية إلى "الاختلاف" للوصول إلى الاستقرار. الفرق يعني إيجاد الفرق بين قيمة في سلسلة زمنية وقيمتها السابقة. وهذا يعادل تقريبا أخذ المشتق. السلسلة الزمنية الثابتة ثابتة بالفعل - تحتاج إلى 0 اختلافات لتصبح ثابتة، لذا فهي I(0). يجب التمييز بين السلسلة الزمنية I(1) مرة واحدة للوصول إلى حالة الثبات.

تم رسم الشكل أعلاه بإجراء فرق على السلسلة الزمنية البرتقالية للحصول على السلسلة الزمنية الزرقاء. وبشكل مكافئ، يتم الحصول على السلسلة الزمنية البرتقالية من خلال دمج السلسلة الزمنية الزرقاء.

تشير عملية جذر الوحدة إلى نماذج الانحدار التلقائي (بشكل أكثر دقة من النوع AR(1)) التي يتم تقدير معلمات rho فيها بـ 1. على الرغم من أنه يمكننا استخدام rho وroot بالتبادل، إلا أن rho يشير إلى القيمة الحقيقية للعملية، والتي عادة ما تكون غير معروفة وتحتاج إلى تقدير. النتيجة المقدرة هي القيمة "الجذر".

تشير قيمة rho إلى مدى تذكر العملية للقيم السابقة. وتشير قيمة u إلى مصطلح الخطأ، الذي يُفترض أنه ضوضاء بيضاء.

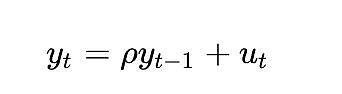
عملية جذر الوحدة هي عملية سير عشوائية وهي عملية غير ثابتة . العمليات ذات قيم "الجذر" أو rho أقل من 1 لا تميل إلى الانحراف وبالتالي فهي ثابتة. وحتى القيم القريبة من (ولكن أقل) 1 تميل إلى أن تعني الارتداد (بدلاً من الانحراف) على المدى الطويل. ومن ثم فإن خصوصية عملية جذر الوحدة هي أنها تختلف جوهريًا عن العمليات التي تكون جذورها قريبة جدًا من 1.

التكامل المشترك بين إشارتين

< p>وجود أو عدم وجود التكامل المشترك (علاقة التكامل المشترك) بين متغيرين عشوائيين (في هذه الحالة، السلاسل الزمنية). لكي يكون لهذا الزوج من المتغيرات علاقة تكامل مشترك، يجب أن يكون لكل منهما نفس ترتيب التكامل ويجب أن يكون كلاهما غير ثابت. علاوة على ذلك (وهذا هو الجزء الأساسي)، يجب أن يكون الجمع الخطي لسلسلتين زمنيتين ثابتًا.

مثال على إشارة بدون تكامل مشترك

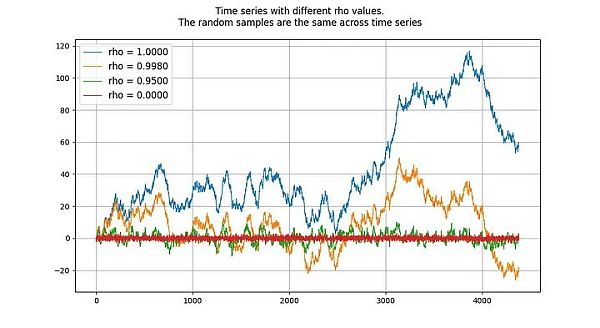
إذا كانت سلسلتان زمنيتان غير ثابتتين، فعندئذ تكون مجموعة خطية (في هذه الحالة، نحتاج فقط إلى اختيار سلسلتين زمنيتين عادة ما يكون الفرق بين السلاسل الزمنية) غير ثابت:

التكامل المشترك مثال إشارة

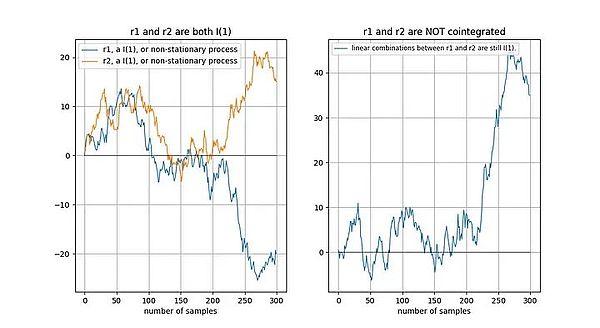
إذا انجرفت سلسلتان زمنيتان غير ثابتتين "بنفس الطريقة" على المدى الطويل، فإن التركيبة الخطية (هنا نختار r2-0.5*r1) هي الممكن ثابت:

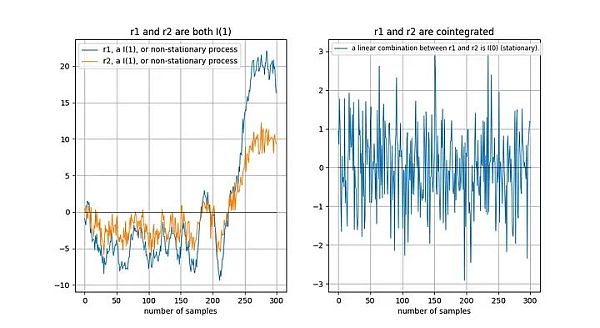
تو وآخرون [1] وصفوا بشكل بديهي علاقة التكامل المشترك:

"إن وجود علاقة تكامل مشترك بين السلاسل الزمنية يعني وجود انجراف عشوائي مشترك بينهما على المدى الطويل".

لماذا يكون الجمع الخطي لسلسلتين زمنيتين غير ثابتتين ثابتًا؟ لنفترض أن لدينا سلسلتين زمنيتين x وy، ونحاول صياغة y بناءً على x: y = a + b*x. يتم إعطاء خطأ النموذج الخاص بنا من خلال المجموعة الخطية من x و y: خطأ النموذج = y - a - b*x . نريد أن يكون خطأ النموذج ثابتًا، أي ألا ينجرف على المدى الطويل. إذا انحرف خطأ النموذج بمرور الوقت، فهذا يعني أن نموذجنا ليس جيدًا ولا يمكنه تقديم تنبؤات دقيقة.

التفاصيل هي الشيطان (التفاصيل تحدد النجاح أو الفشل)

في إنجل وجرانجر [2] (جرانجر هو الاختراع) لمفهوم التكامل المشترك في مقالته "التكامل المشترك وتصحيح الأخطاء: التمثيل والتقدير والاختبار" (الذي فاز بجائزة نوبل في الاقتصاد عام 2003)، حدد المفاهيم الأساسية وطرق اختبار التكامل المشترك. مفتاح هذه الورقة هو الافتراض بأن السلسلة الزمنية عشوائية ولا تحتوي على عنصر حتمي (سنصل إلى ذلك لاحقًا).

في حالة وجود اتجاه حتمي، يجب إزالته قبل التحليل:

يتم تطبيقه على الوقت وسعر البيتكوين

في قانون القوة المبني على الزمن، لدينا متغيران:

1.log_time: لوغاريتم عدد الأيام منذ كتلة التكوين

2.log_price: السعر اللوغاريتم of

وفقًا لتعريفات إنجل وجرانجر، يجب أن يكون كلا المتغيرين متغيرين عشوائيين، وليس لهما مكونات حتمية، ويجب أن يكونا غير ثابتين. علاوة على ذلك، يجب أن نكون قادرين على إيجاد مزيج خطي ثابت من هذين المتغيرين. وبخلاف ذلك لا توجد علاقة تكامل مشترك بين المتغيرين.

قبل أن نتعمق في التفاصيل، دعونا نعرض بعض الرسوم البيانية لبيانات النموذج نفسها، والتي لا تتضمن أي مفهوم للثبات أو التكامل المشترك. لاحظ أن قانون القوة المبني على الزمن ينتج توافقًا يبدو جيدًا بشكل بديهي. لا يُظهر ناقل البقايا الانجراف على الفور.

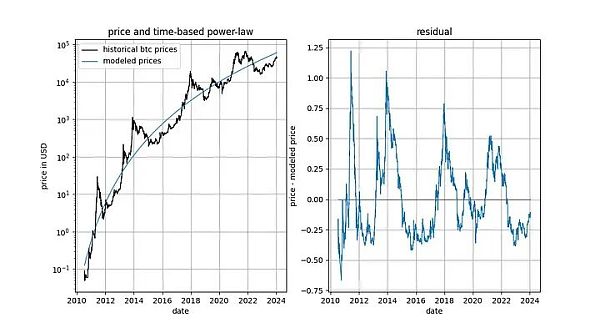
بالإضافة إلى ذلك، يُظهر النموذج أيضًا أداءً ممتازًا خارج العينة (انظر أقل) . لا يعني الأداء الممتاز خارج العينة أن النموذج زائف - فالنموذج القائم على الارتباطات الزائفة يجب أن يكون ببساطة زائفًا، أي يفشل في التنبؤ بدقة. تتمثل إحدى طرق فحص الأداء خارج العينة في ملاءمة النموذج لكمية محدودة من البيانات (اعتبارًا من تاريخ معين) وإجراء تنبؤات للفترات الزمنية التي لا يكون فيها النموذج مناسبًا (على غرار التحقق من الصحة المتبادل). خلال فترة خارج العينة، كثيرًا ما تتقاطع الأسعار المرصودة مع الأسعار النموذجية، ولا تتحرك أكبر الانحرافات في الأسعار المرصودة بشكل منهجي بعيدًا عن الأسعار النموذجية.

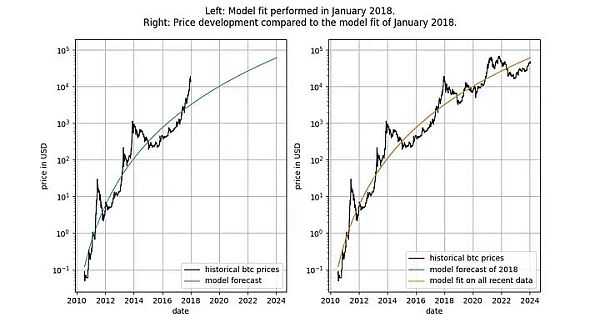
يمكننا أن نكون أكثر صرامة ونلاحظ النتائج بعد إصدار النموذج (سبتمبر) 2019) الأداء، لأنه بعد إصدار النموذج، لا يمكننا الغش بأي شكل من الأشكال - لا يمكننا تغيير النموذج بعد وقوعه.

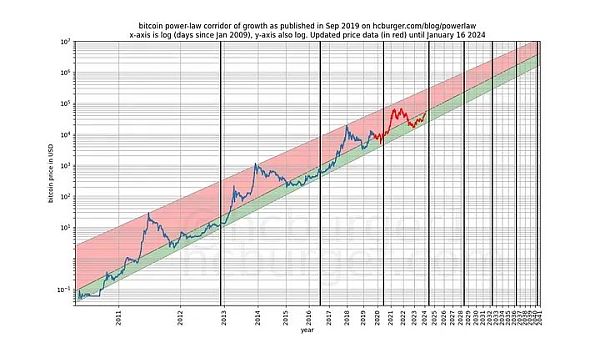
إذا اتهم أي شخص النموذج بأنه يعتمد فقط على ارتباط خاطئ، فهذا يعني أن يجب أن تكون القوة التنبؤية للنموذج موضع شك بالفعل.

تحقيق التكامل المشترك تدريجيًا

لجعل من الممكن وجود علاقة تكامل مشترك بين log_time وlog_price، يجب أن يكون المتغيران متغيرين عشوائيين بنفس الترتيب وهو متغير عشوائي من الرتبة 1 على الأقل.

متغير سعر السجل

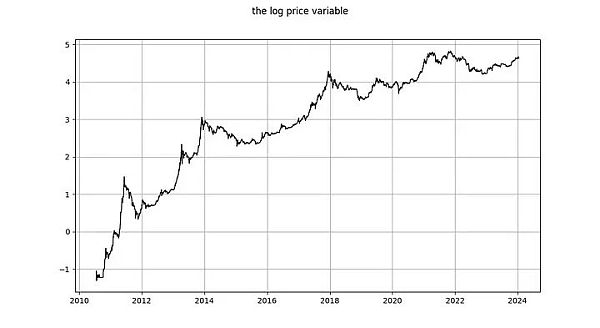
هل log_price سلسلة زمنية ثابتة؟ يستخدم Nick اختبار ADF غير المحدد (اختبار عدم الثبات) واختبار KPSS (اختبار الثبات) لاستنتاج أن السجل (السعر) غير ثابت بلا شك وبالتالي I(1) أو أعلى. استنتج مارسيل برجر بالفحص البصري أنه أنا (1). يقدم تيم ستولت ملاحظة أكثر إثارة للاهتمام: فهو يقوم بإجراء اختبار ADF (نوع غير محدد) لفترات مختلفة ويشير إلى أن الموقف ليس واضحًا: "لذلك لا يمكننا أن نرفض بشدة عدم الاستقرار ونستنتج أن هناك عدم استقرار في السجل - استنتاجات السعر لعلامات الجمود."

دعونا نجري التحليل بأنفسنا. كما هو الحال مع Tim Stolte، سنقوم بإجراء اختبار ADF على نوافذ زمنية مختلفة: بدءًا دائمًا من أول تاريخ متاح وزيادة بمقدار يوم واحد كل يوم (نستخدم البيانات اليومية). بهذه الطريقة، يمكننا أن نرى كيف تتغير نتائج اختبار وحدة التغذية التلقائية للمستندات بمرور الوقت. ولكن على عكس تيم ونيك، نريد تحديد إصدار اختبار ADF الذي سيتم تشغيله. وفقًا لويكيبيديا، هناك ثلاثة أنواع رئيسية من اختبارات DF وADF:

هذه تختلف الإصدارات الثلاثة في قدرتها على استيعاب (إزالة) الاتجاهات المختلفة. يرتبط هذا بمتطلبات إنجل وجرانجر لإزالة أي اتجاهات حتمية - هذه الإصدارات الثلاثة قادرة على إزالة ثلاثة أنواع بسيطة من الاتجاهات الحتمية. يحاول الإصدار الأول وصف التغيرات اليومية في سعر السجل باستخدام بيانات سعر السجل السابقة فقط. يسمح الإصدار الثاني باستخدام مصطلح ثابت، مع تأثير أن log_price يمكن أن يكون له اتجاه خطي (إما لأعلى أو لأسفل). الإصدار الثالث يسمح بالمكونات التربيعية (المكافئة).

لا نعرف الإصدار الذي يستخدمه Tim وNick، ولكننا سنقوم بتشغيل الثلاثة جميعًا.

الحد الأقصى للتأخير الذي نستخدمه في اختبارات وحدة التغذية التلقائية للمستندات (ADF) لدينا هو 1، ولكن استخدام الفترات الزمنية الأطول لا يغير نتائجنا واستنتاجاتنا بشكل ملموس. سوف نستخدم دالة statsmodels.tsa.stattools.adfuller الخاصة ببايثون مع "maxlag" بقيمة 1 و"n" و"c" و"ct" (أي ما يعادل الأنواع الثلاثة الموضحة أعلاه في ويكيبيديا) لمعلمة "regression". في الصورة أدناه، نعرض القيمة p (مقياس للأهمية الإحصائية) التي تم إرجاعها بواسطة الاختبار، مع قيم p أصغر تشير إلى احتمالية أكبر للثبات (القيمة الحرجة شائعة الاستخدام هي 0.05).

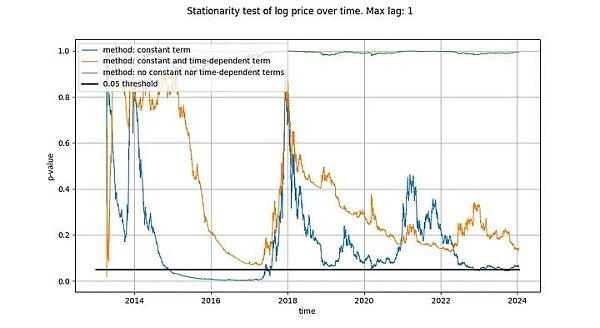
لاحظنا أن الاستنتاج الذي تم استخلاصه بالطريقة الأولى (الخط الأخضر) نعم، السلسلة الزمنية log_price غير ثابتة. إن نتيجة الاختبار الثالث (الخط البرتقالي) هي نفسها، ولكنها أقل حسما. ومن المثير للاهتمام أن الاختبار الذي يسمح بمصطلح ثابت (الخط الأزرق) لا يمكنه معرفة ما إذا كانت السلسلة الزمنية ثابتة (على الأرجح استخدم تيم أيضًا اختبار ADF بمصطلح ثابت). لماذا تختلف هذه الإصدارات الثلاثة كثيرًا، وعلى وجه الخصوص لماذا لا يمكن للإصدار ذو المصطلح الثابت أن يستبعد أن log_price ثابت؟

هناك تفسير واحد فقط: استخدام مصطلح ثابت فقط في فرق log_price (مما يؤدي إلى مصطلح خطي في log_price) يناسب السلسلة الزمنية "جيدًا"، مما يؤدي إلى إشارة متبقية تبدو ثابتة تقريبًا (على الرغم من الانحراف بين نقطتي البداية والنهاية كبير جدًا). إن عدم استخدام الاتجاهات الحتمية في log_price على الإطلاق، أو استخدام التأثيرات الحتمية للمصطلح التربيعي، أقل فعالية بكثير.

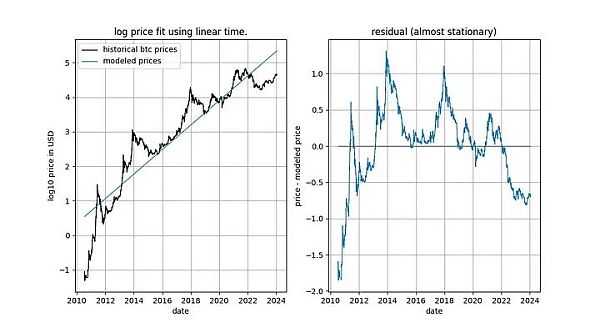
لقد أعطانا هذا تلميحًا قويًا إلى أن العلاقة بين الوقت وlog_price موجودة علاقة. في الواقع، إذا خلص اختبار ADF باستخدام مصطلح ثابت إلى أن الإشارة ثابتة، فهذا يعني أن المصطلح الزمني الخطي يقترب جيدًا من log_price، مما يؤدي إلى بقايا ثابتة. يعد الحصول على المخلفات الثابتة أمرًا مرغوبًا فيه لأنه علامة على وجود علاقة غير زائفة (أي أننا وجدنا المتغيرات التفسيرية الصحيحة). إن الاتجاه الزمني الخطي ليس هو ما نريده تمامًا، ولكن يبدو أننا نقترب منه.

تختلف استنتاجاتنا بشكل كبير عن استنتاجات مارسيل برجر، الذي قال (في مقال آخر):

"في تحليل سابق، أوضحت أن عملة البيتكوين تظل صالحة لأن "سعر البيتكوين متكامل من الدرجة الأولى. ولا تظهر عملة البيتكوين أي عناصر حتمية في تطور سعرها بمرور الوقت."

استنتاجنا هو أن الوقت الخطي لا يفسر بشكل كامل سلوك سعر البيتكوين على مر الزمن. الوقت، ولكن من الواضح تمامًا أن log_price له عنصر زمني محدد. علاوة على ذلك، ليس من الواضح ما إذا كان log_price هو I(1) بعد إزالة المكونات الحتمية المناسبة (كما هو مطلوب من قبل Engle وGranger). وبدلا من ذلك، يبدو أن الاتجاه ثابت، ولكن لا يزال يتعين علينا العثور على عنصر حتمي مناسب.

إذا كنا نبحث عن علاقة تكامل مشترك، فمن الصعب بالفعل أن يكون log_price ليس I(1)، لأنه لكي يتم التكامل المشترك بين متغيرين، يجب أن يكون كلاهما I(1) أو أعلى.

متغير وقت السجل

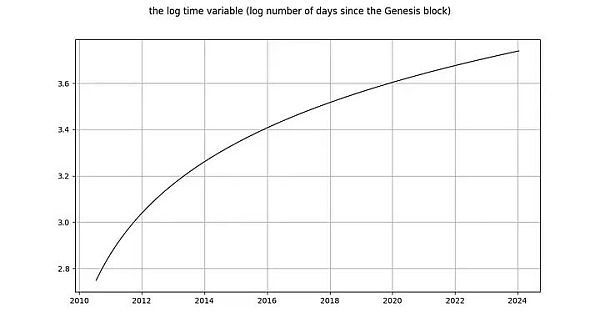
الآن دعونا نلقي نظرة على المتغير log_time. استنتج مارسيل برجر أن log_time يبدو وكأنه يتكامل مع الترتيب 6 (كان يقوم بالتمايز حتى واجه مشاكل عددية). إن توقعه بأن دالة رياضية مثل اللوغاريتم يمكن أن تتحول من متغير حتمي تمامًا إلى متغير عشوائي لم يكن له أي معنى.

الاستنتاج الذي توصل إليه Nick بشأن log_time هو نفسه بالنسبة لمتغير log_price: فهو بلا شك غير ثابت وبالتالي I(1) أو أعلى. يدعي تيم ستولت أن log_time غير ثابت من خلال البناء. هذه التصريحات مثيرة للدهشة! يشير النظام التكاملي والتكامل المشترك إلى مفهوم المتغيرات العشوائية التي تم فيها التخلص من أي اتجاه حتمي (انظر إنجل وجرانجر [2] أعلاه). ما يجب التذكير به هو أن قيمة المتغير الحتمي معروفة مسبقًا، في حين أن قيمة المتغير العشوائي غير معروفة. الوقت (من الواضح) حتمي تمامًا، وكذلك الدالة اللوغاريتمية، لذا فإن log_time هو أيضًا حتمي تمامًا.

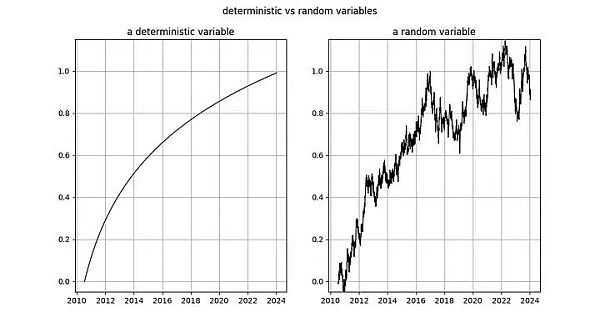
الرسم التوضيحي: اليسار: لوغاريتم عدد الأيام منذ كتلة التكوين حتمية تمامًا. اليمين: متغير عشوائي (يشبه إلى حد ما المتغير الحتمي الموجود على اليسار).

إذا اتبعنا طريقة إنجل وجرانجر وقمنا بإزالة الاتجاه الحتمي من log_time، فإن ما يتبقى هو متجه صفر، حيث أن log(x) - log(x) = 0 ، أي، لا يزال لدينا إشارة مؤكدة تماما. هذا يعني أننا عالقون - لا يمكننا تحويل log_time، وهو متغير حتمي تمامًا، إلى متغير عشوائي، لذلك لا يمكننا استخدام إطار عمل Engle وGranger.

هناك طريقة أخرى لمعرفة مدى إشكالية المتغير الحتمي الكامل في تحليل التكامل المشترك وهي النظر في كيفية تعامل اختبار الثبات مثل اختبار ديكي فولر معه. لنفكر في أبسط حالة (حيث y هو المتغير محل الاهتمام، وrho هو المعامل الذي سيتم تقديره، وu هو مصطلح الخطأ المفترض أنه ضوضاء بيضاء):

ماذا سيحدث؟ مصطلح الخطأ u_{t} هو 0 لجميع قيم t لأنه ليس لدينا مكون عشوائي - لا داعي للخطأ. ولكن بما أن log_time هي دالة غير خطية للوقت، فإن قيمة rho يجب أن تعتمد أيضًا على الوقت.

يعد هذا النموذج أكثر فائدة للمتغيرات العشوائية لأن المتغير rho يلتقط مدى تذكر القيم العشوائية السابقة. ولكن بدون قيم عشوائية، فإن النموذج لا معنى له.

بالنسبة للمتغيرات الحتمية، فإن الأنواع الأخرى من الاختبارات لها نفس المشكلة.

لذلك، فإن المتغيرات الحتمية تمامًا لا تنتمي إلى نطاق تحليل التكامل المشترك. أو بعبارة أخرى: تحليل التكامل المشترك لا يعمل مع الإشارات الحتمية، وإذا كانت إحدى الإشارات حتمية، فإن تحليل التكامل المشترك هو أداة عفا عليها الزمن وتدعي وجود علاقة زائفة.

كيفية الشرح

توجد علاقة التكامل المشترك فقط عندما يكون كلا المتغيرين I(d) وd يساوي 1 على الأقل. لقد أظهرنا أن log_time متغير حتمي تمامًا ولا يمكن استخدامه للاختبار الثابت. لا يمكننا معرفة ما إذا كان log_time هو I(0) أو I(1) أو I(6). بالإضافة إلى ذلك، log_price ليس I(1)، ولكنه ذو اتجاه ثابت.

لا توجد علاقة تكامل مشترك بين log_time وlog_price. هل هذا يعني أن قوانين القوة المستندة إلى الوقت غير صالحة إحصائيًا أو زائفة؟

بالطبع لا

في أي تحليل إحصائي مناسب، من الصحيح تمامًا استخدام المتغيرات الحتمية المختلطة والمتغيرات الثابتة الاتجاهية ل. التكامل المشترك ليس، كما يريد منتقدونا أن يعتقدوا، نقطة مركزية في تحليل العلاقات الإحصائية.

لذلك، تحليل التكامل المشترك غير ممكن. ومع ذلك، قد يكون هناك مكان للتحليل الثابت المطبق على نماذج قانون السلطة. دعونا استكشاف هذا أبعد من ذلك.

السبب وراء قيامنا أولاً بإجراء تحليل التكامل المشترك على متغيرات المدخلات هو أننا نأمل في العثور على مجموعة خطية ثابتة من الاثنين. من المستحيل بشكل أساسي الجمع بين المتغير الحتمي (log_time) ومتغير الاتجاه الثابت (log_price) للحصول على متغير ثابت. لذلك، بدلاً من البحث عن علاقة تكامل مشترك بالمعنى الدقيق للكلمة، يمكننا ببساطة إجراء اختبار ثبات على البقايا (نظرًا لأن البقايا هي مجرد مزيج خطي من إشارتي الإدخال). إذا كانت البقايا ثابتة، فإننا نجد مجموعة خطية ثابتة على الرغم من أننا لا نتبع بدقة اختبار التكامل المشترك إنجل جرانجر (والذي هو الغرض من التكامل المشترك).

مناقشة متعمقة

يشرح جيمس ج. ماكينون [3] هذا بالضبط في ورقته "القيم الحرجة لاختبارات التكامل المشترك": إذا كان A يتم إجراء "انحدار التكامل المشترك" (الانحدار الذي يربط وقت السجل بسعر السجل)، ثم اختبار التكامل المشترك (اختبار إنجل جرانجر) هو نفس اختبار ثبات البقايا (اختبار DF أو ADF):< p>

كرر MacKinnon هذا البيان: إذا كانت المعلمات التي تربط log_time وlog_price بديهية، إذا كنت تعرف، فيمكنك ذلك تخطي اختبار التكامل المشترك Engle-Granger وقم بدلاً من ذلك بإجراء أحد الأنواع الثلاثة الشائعة لاختبارات الاستقرار (اختبار DF أو ADF) على البقايا:

لذلك، يمكننا استخدام أي من الطريقتين، باستثناء إحصائية الاختبار الناتجة. فهي نفسها:

1. قم بمطابقة log_time وlog_price واحسبها المتبقي (الخطأ). احسب DF، أو الأفضل من ذلك اختبار ADF، من المخلفات. توضح الإحصائية الناتجة ما إذا كانت البقايا ثابتة أم لا.

2. افترض أن log_time وlog_price هما I(1) وقم بإجراء اختبار التكامل المشترك Engel-Granger. يمكن أن تشير الإحصائيات الناتجة أيضًا إلى ما إذا كانت البقايا ثابتة أم لا.

بالنسبة لاختبار ADF، نستخدم وظيفة statsmodels.tsa.stattools.adfuller الخاصة ببايثون؛ وبالنسبة لاختبار Engle-Granger، نستخدم statsmodels.tsa.stattools.coint. بالنسبة لكلتا الوظيفتين، استخدمنا طريقة عدم استخدام ثابت (عدم الانجراف مع مرور الوقت) لأن المتبقي لدينا لا ينبغي أن يحتوي على الانجراف مع مرور الوقت (لأن هذا يعني أنه مع مرور الوقت، يبدأ النموذج في المبالغة في تقدير السعر أو التقليل منه).

لقد كتبنا أن اختبار ADF واختبار Engle-Granger متكافئان، ولكن هذا ليس هو الحال: فهما لا ينتجان نفس إحصائيات الاختبار. يفترض اختبار التكامل المشترك Engle-Granger أن N = 2 متغيرات عشوائية، بينما يفترض اختبار ADF أن N = 1 متغيرات عشوائية (N هو مقياس درجات الحرية). يمكن أن يتأثر المتغير العشوائي بمتغير عشوائي آخر أو بمتغير حتمي، لكن المتغير الحتمي لا يمكن أن يتأثر بمتغير عشوائي. ولذلك، في حالتنا (مع متغير حتمي واحد فقط log_time)، تكون الإحصائية التي يتم إرجاعها بواسطة اختبار ADF (بافتراض N = 1 متغيرات عشوائية) هي الأفضل. من حيث المبدأ، قد يختلف اختبار Engle-Granger واختبار ADF، ولكن في النماذج المستندة إلى الوقت، ليس هذا هو الحال في الممارسة العملية. كما هو موضح في الشكل أدناه، فإن الاستنتاج هو نفسه: نحصل على ناقل متبقي ثابت. وكانت درجات كلا الاختبارين أقل بكثير من القيمة الحرجة 0.05 (مما يشير إلى أن البقايا ثابتة)، وظلت كذلك لفترة طويلة.

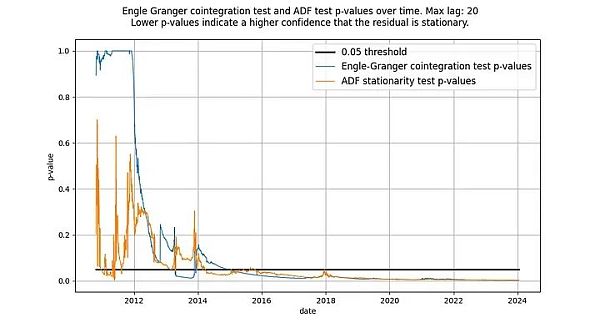
رسم توضيحي: قانون الطاقة المبني على الزمن له بقايا ثابتة بدءًا من عام 2016 تقريبًا، وفقًا لاختبارات ADF وEngle-Granger.

لم يظهر أي من الاختبارين في البداية أن البقايا الثابتة كانت طبيعية. وذلك لأن المكونات ذات التردد المنخفض في الإشارة المتبقية يمكن أن يتم الخلط بينها وبين إشارات غير ثابتة. ومع مرور الوقت فقط، يصبح متوسط ​​الارتداد للمخلفات واضحًا، وفي الواقع، ثابتًا.

أسعار S2F وأسعار مؤشرات الأسهم طويلة الأجل

تم رفض نموذج S2F عمومًا، على ما يبدو بسبب إثبات استحالة التكامل المشترك بالمعنى الدقيق للكلمة. على غرار قانون القوة المستند إلى الوقت: تكون متغيرات الإدخال حتمية (جزئيًا). ومع ذلك، فإن النموذج ينتج بقايا تبدو ثابتة جدًا.

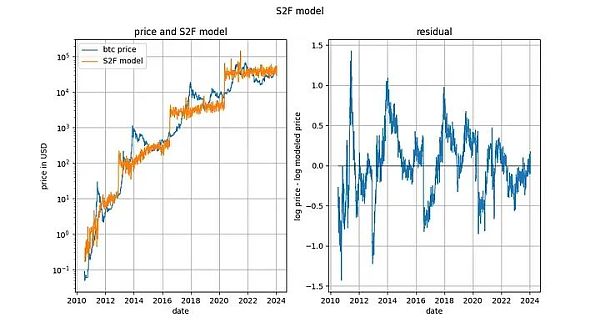
في الواقع، اختبار التكامل المشترك Engle-Granger واختبار ثبات ADF (لأنه هناك متغير حتمي ومتغير عشوائي، لذلك هو الأفضل) والقيم الاحتمالية الناتجة كلها قريبة جدًا من 0. ولذلك، لا ينبغي استبعاد نماذج S2F على أساس "الافتقار إلى التكامل المشترك" (في الواقع "الافتقار إلى الثبات").

ومع ذلك، لاحظنا في أوائل عام 2020 أن هناك دلائل أخرى على أن نموذج S2F لم يصمد. لقد ثبت أن توقعاتنا بأن سعر BTCUSD سيكون أقل مما توقعه نموذج S2F كانت بعيدة النظر.

من المثير للاهتمام أيضًا النظر إلى مؤشرات أسعار الأسهم طويلة الأجل مقابل الوقت (هنا مؤشر S&P 500 بدون إعادة استثمار الأرباح). ليس سراً أن مؤشرات أسواق الأسهم الرئيسية تنمو بمعدل أسي متوسط ​​يبلغ حوالي 7٪. في الواقع، لقد أكدنا ذلك أيضًا من خلال الانحدار الأسي.

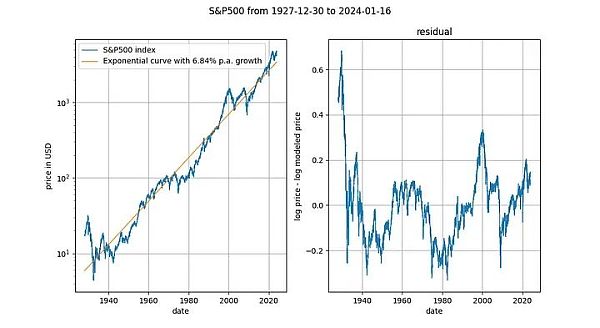
هنا نواجه متغيرًا حتميًا آخر (الوقت). يعطي اختبار التكامل المشترك Engle-Granger قيمة p تبلغ حوالي 0.025، ويعطي اختبار ADF (المفضل) قيمة p تبلغ حوالي 0.0075 (لكن هذه القيم تعتمد بشكل كبير على الفترة الزمنية المحددة المختارة). مرة أخرى، بقايا ثابتة. الاتجاهات الزمنية الأسية في أسعار الأسهم صالحة.

التأثير

كان نموذج S2F يحظى بتقدير كبير في البداية (خاصة من قبل مارسيل برجر ونيك إمبلو) بسبب أساسه الاقتصادي القياسي الجيد المزعوم، وخاصة وجود علاقات التكامل المشترك. مع تحول المد، أصبح من الواضح أن نموذج S2F لم يكن متكاملاً بشكل صارم، وقفز كل من مارسيل ونيك من السفينة، معلنين أن نموذج S2F غير صالح. ويبدو أن الرأي العام حول نموذج S2F تغير أيضًا بعد هذه الحادثة. لدى إريك وول ملخص قصير وممتاز لتطور الأحداث.

لقد أوضحنا، وتتفق معنا أدبيات الاقتصاد القياسي (ماكينون [3])، أنه يمكن استخدام التكامل المشترك والثبات بشكل متبادل تقريبًا (باستثناء قيمة الإحصائية). وتمشيا مع هذا الرأي، لا نعتقد أن نموذج S2F لديه أي مشاكل مع التكامل المشترك/الثبات، وبالتالي سيكون من الخطأ تغيير وجهة نظر المرء بشأن نموذج S2F بسبب الافتقار المزعوم للتكامل المشترك. نحن نتفق على أن نموذج S2F خاطئ، ولكن سبب خطأه ليس الافتقار إلى التكامل المشترك.

تعرض نموذج قانون القوة الخاص بالبيتكوين للوقت لانتقادات بسبب افتقاره إلى التكامل المشترك، والذي يقال إنه يشير إلى أن العلاقة بين log_time وlog_price زائفة. لقد أظهرنا أن بقايا نموذج قانون القوة القائم على الزمن الخاص بالبيتكوين ثابتة بشكل واضح، وبالتالي فإن منطق النقاد مشكوك فيه.

يعتبر نموذج قانون قوة الوقت الخاص بالبيتكوين فعالاً ومستقرًا وقويًا. كما هو الحال دائما.

المراجع

1. "التكامل المشترك العالمي وتطبيقاته" Tu et al.، بما في ذلك معلومات تكميلية

2. "التكامل المشترك وتصحيح الأخطاء: التمثيل والتقدير والاختبار" بقلم روبرت إف إنجل وسي دبليو جي. جرانجر

3. "القيم الحرجة لاختبارات التكامل المشترك"، جيمس ج. ماكينون

< ع >