أحدث مقال لفيتاليك: استكشاف دائرة ستاركس

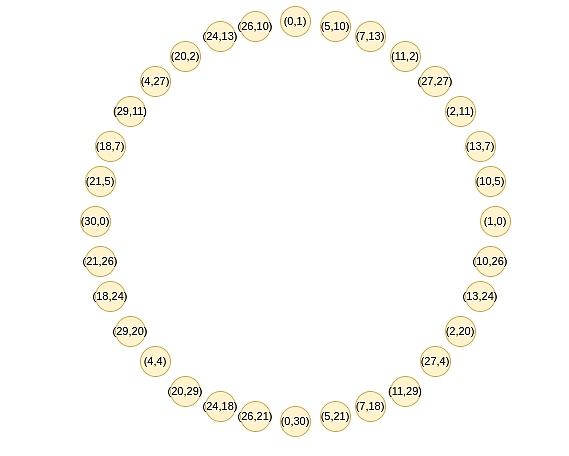
تتبع هذه النقاط قانون الجمع، وإذا كنت قد درست مؤخرًا علم المثلثات أو الضرب المعقد، فقد تجد هذا القانون مألوفًا:

- https://unacademy.com/content/cbse-class- 11/study -material/mathematics/algebra-of-complex-numbers-multiplication/

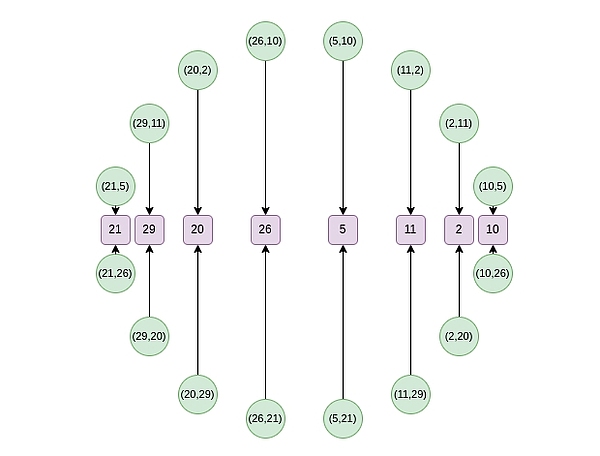
من الجولة الثانية فصاعدًا، يتغير التعيين:

دائرة FFTs

• https://vitalik.eth.limo/general/2019/05/12/fft.html< القسم>

• https://www.researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_Finite_Fields

من هنا، دعنا ندخل في بعض التفاصيل الباطنية، لأولئك الذين ينفذون دائرة STARK، مقابل هذه التقليدية ستكون التفاصيل مختلفة مقارنة بـ STARK.

بدء الأعمال

• https:/ /eprint.iacr.org/2019/336

كثيرة الحدود المتلاشية

ترتيب البت العكسي

الكفاءة

لذلك، ضع دائرة حول STARK هو في الواقع قريب جدًا من الأمثل! يعتبر Binius أكثر قوة لأنه يسمح بخلط ومطابقة النطاقات ذات الأحجام المختلفة، مما يوفر تعبئة أكثر كفاءة لكل شيء. يوفر Binius أيضًا خيار إجراء إضافات 32 بت دون تحميل جدول البحث. ومع ذلك، فإن هذه المكاسب تأتي على حساب (في رأيي) تعقيد نظري أعلى بكثير، في حين أن دائرة STARK (و STARK العادية المستندة إلى BabyBear) بسيطة من الناحية المفاهيمية.

الخلاصة: ما رأيي في دائرة ستارك؟

مقارنة بـ STARK العادي، لا تجلب Circle STARK الكثير من التعقيد الإضافي للمطورين. أثناء عملية التنفيذ، فإن المشكلات الثلاث المذكورة أعلاه هي في الأساس الاختلافات الوحيدة التي أراها مقارنةً بـ FRI التقليدية. إن الرياضيات وراء "متعددات الحدود" التي تعمل عليها Circle FRI هي غير بديهية تمامًا وتستغرق بعض الوقت لفهمها وتقديرها. ولكن يحدث أن يكون هذا التعقيد مخفيًا حتى لا يرى المطورون الكثير منه. إن تعقيد الرياضيات الدائرية مغلف، وليس منهجي.

• https://vitalik.eth.limo/general/2022/02/28/ تعقيد.html

يعد فهم دائرة FRI ودائرة FFT أيضًا أسلوبًا فكريًا جيدًا لفهم "FFTs الغريبة" الأخرى: الأكثر تجدر الإشارة إلى مجال ثنائي FFT، تم استخدامه سابقًا في Binius وLibSTARK، بالإضافة إلى بنيات أكثر غرابة، مثل المنحنى الإهليلجي FFT، الذي يستخدم تعيينات متعددة ويعمل بشكل جيد مع عمليات نقطة المنحنى الإهليلجي.

• https://github.com/ethereum/research/blob/master/binius/ ثنائي_ntt.py#L60

• https://github.com/elibensasson/libSTARK

• https://arxiv.org/abs/2107.08473

من خلال الجمع بين Mersenne31 وBabyBear وتكنولوجيا النطاق الثنائي مثل باعتبارنا Binius، نشعر أننا نقترب من حدود كفاءة "الطبقة الأساسية" لـ STARK. في هذا الوقت، أتوقع أن تتحول حدود تحسين STARK نحو الحساب الأكثر كفاءة للبدائيات مثل وظائف التجزئة والتوقيعات (وتحسين تلك البدائيات نفسها لهذا الغرض)، والإنشاءات العودية لفتح المزيد من الموازاة، وحساب الأجهزة الافتراضية لتحسين تجربة المطور، وغيرها من المهام عالية المستوى.