طريقة تمويل آمنة للشركات الناشئة
SAFT وSAFE هي طرق تمويل بسيطة ومرنة وفعالة، ولا تستغرق سوى بضع صفحات. يتم استخدام SAFT لرفع حقوق العملة، ويتم استخدام SAFE لرفع حقوق الملكية.
 JinseFinance
JinseFinance
المصدر: مجتمع Denglian
مقدمة لبرامج ZKP التعليمية للمبرمجين العاملين.
هل تعلم لماذا تمتلك الحمير الوحشية خطوطًا؟ إحدى النظريات هي أنه تمويه. عندما تتجمع الحمير الوحشية معًا، فإن ذلك يجعل من الصعب على الأسود التمييز بين فرائسها. يجب على الأسود أن تعزل فرائسها عن المجموعة لتتمكن من ملاحقتها[^1].
يحب البشر أيضًا الاختباء وسط الحشود. مثال محدد هو عندما يعمل عدة أفراد كوحدة تحت اسم جماعي. هذه هي الطريقة التي تم بها إنشاء الأوراق الفيدرالية[^2]. مثال آخر هو بورباكي، الاسم المستعار الجماعي لمجموعة من علماء الرياضيات الفرنسيين في الثلاثينيات. أدى ذلك إلى إعادة كتابة كاملة لكثير من الرياضيات الحديثة، مع التركيز على الدقة والأساليب البديهية[^3].
في العصر الرقمي، تخيل أنك في محادثة جماعية وتريد إرسال رسالة مثيرة للجدل. تريد أن تثبت أنك واحد منهم دون الكشف عن أي منهم. كيف يمكننا القيام بذلك في المجال الرقمي باستخدام التشفير؟ يمكننا استخدام شيء يسمى توقيع المجموعة.
تقليديًا، تكون التوقيعات الجماعية معقدة رياضيًا ويصعب تنفيذها. ومع ذلك، باستخدام إثباتات المعرفة الصفرية (ZKP)، تصبح هذه المشكلة الرياضية مهمة برمجة بسيطة. بحلول نهاية هذه المقالة، ستتمكن من كتابة توقيع مجموعتك الخاصة.
ستوضح لك هذه المقالة كيفية كتابة إثبات المعرفة الصفرية الأساسي (ZKP) من البداية.
عند تعلم حزمة تقنية جديدة، نريد إتقان دورة التحرير والإنشاء والتشغيل في أسرع وقت ممكن. وعندها فقط يمكننا أن نبدأ في التعلم من تجاربنا.
سنطلب منك أولاً إعداد البيئة الخاصة بك، وكتابة برنامج بسيط، وتنفيذ ما يسمى بالإعداد الموثوق به، ثم إنشاء البراهين والتحقق منها في أسرع وقت ممكن. وبعد ذلك، سنتعرف على بعض الطرق لتحسين برنامجنا، وتنفيذ هذه التحسينات، واختبارها. في هذه العملية، سنقوم ببناء نموذج عقلي أفضل لبرمجة ZKPs عمليًا. في نهاية المطاف، سوف تصبح مألوفًا (بطريقة أو بأخرى) لكتابة ZKP من الصفر.
سنبني خطوة بخطوة نظام توقيع بسيط يمكنك استخدامه لإثبات أنك أرسلت رسالة محددة. ستكون قادرًا على فهم ما يفعله هذا الرمز ولماذا:
# استنساخ المستودع وتشغيل الإعداد script
git clone git@github.com:oskarth/zkintro-tutorial.git
cd zkintro-tutorial
;
# تصفح محتويات هذا الملف قبل التنفيذ
less ./scripts/prepare.sh
./scripts/prepare.sh
نوصي بتصفح ./scripts/prepare.sh< /code> لمعرفة ما سيتم تثبيته، أو إذا كنت تفضل التثبيت يدويًا، بعد التنفيذ، يجب أن ترى اكتمل التثبيت ولا توجد أخطاء.
إذا واجهت مشاكل، يرجى مراجعة أحدث الوثائق الرسمية هنا [7]. بمجرد الانتهاء، يجب أن يكون لديك الإصدار التالي مثبتًا (أو أعلى):
pragma circom 2.0.0;
قالب Multiplier2 () {< br> إدخال الإشارة a;
إدخال الإشارة b; ; <== * b;
component main = Multiplier2();
هذا هو برنامجنا الخاص أو _الدائرة_. [^6] التحليل سطرًا بسطر:
pragma circom 2.0.0; - يحدد الدائرة الإصدار المستخدم
template Multiplier() - القوالب تعادل الكائنات في معظم لغات البرمجة وهي شكل شائع من أشكال التجريد
إدخال الإشارة أ; - الإدخال الأول لدينا، a؛ يكون الإدخال خاصًا بشكل افتراضي
إدخال الإشارة b; - إدخالنا الثاني، b يكون خاصًا أيضًا بشكل افتراضي
- < p>؛
مخرج الإشارة ب; - مخرجنا، c; المخرج دائمًا عام c <= = a * b; - يؤدي ذلك إلى شيئين: تعيين الإشارة c إلى و تقييد c ليكون مساويًا لـ < Product of code>ab
component main = Multiplier2() - يقوم بإنشاء مثيل للمكون الرئيسي p>
السطر الأكثر أهمية هو c <== a * b;. هذا هو المكان الذي نعلن فيه القيود فعليًا. هذا التعبير هو في الواقع مزيج من اثنين: <-- (المهمة) و=== (قيد المساواة). [^7] يمكن للقيود في Circom فقط استخدام العمليات التي تتضمن الثوابت أو الجمع أو الضرب. ويفرض أن طرفي المعادلة يجب أن يكونا متساويين. [^8]
كيف تعمل القيود؟ في سياق يشبه سودوكو، قد نقول أن القيد هو "رقم بين 1 و9". ومع ذلك، في سياق Circom، هذا ليس قيدًا واحدًا، ولكنه شيء يتعين علينا التعبير عنه باستخدام مجموعة أبسط من قيود المساواة (===). [^9]
لماذا هذا؟ هذا له علاقة بالمبادئ الرياضية الأساسية. بشكل أساسي، تستخدم معظم ZKPs _الدوائر الحسابية_، والتي تمثل حساب متعددات الحدود. عند العمل مع كثيرات الحدود، يمكنك بسهولة إدخال الثوابت وإضافتها وضربها والتحقق مما إذا كانت متساوية. [^10] يجب التعبير عن العمليات الأخرى من حيث هذه العمليات الأساسية. لا يتعين عليك معرفة ذلك بالتفصيل لكتابة ZKP، ولكن قد يكون من المفيد معرفة ما يحدث تحت الغطاء. [^11]
يمكننا تصور الدائرة على النحو التالي:

للرجوع إليها، يمكن العثور على الملف النهائي في example1-solution.circom. لمزيد من التفاصيل حول بناء الجملة، راجع الوثائق الرسمية [9].
يمكننا تجميع دائرتنا عن طريق تشغيل الأمر التالي:

هذه دعوة بسيطة لـ circom لإنشاء example1.r1cs وexample1.wasm حزمة الملفات. من المفترض أن ترى شيئًا مشابهًا لما يلي:
< كود> {
"pi_a": ["15932[...]3948", "66284[.. .]7222"، "1"],
"pi_b": [
; ["17667[...]0525", "13094[...]1600"],
["12020[" ...]5738"، "10182[...]7650"],
["1"، "0"]
],
"pi_c":["18501[...]3969", ;" 13175[...]3552", "1"],
"البروتوكول": "groth16",
"curve": "bn128"
يعتمد هذا على بعض الكائنات الرياضية (ثلاثة يتم تحديد الدليل في شكل عناصر منحنى إهليلجي) pi_a، pi_b، وpi_c. [^20] يتضمن أيضًا بيانات وصفية حول البروتوكول (groth16) و_curve_ المستخدم (bn128، وهي تفاصيل تنفيذ رياضية سنتجاهلها في الوقت الحالي). يتيح ذلك للمدقق معرفة ما يجب فعله بهذا الدليل للتحقق بشكل صحيح.
لاحظ مدى إيجاز الدليل؛ وبغض النظر عن مدى تعقيد برنامجنا الخاص، فسيكون بهذا الحجم فقط. يوضح هذا خاصية الإيجاز الخاصة بـ ZKPs التي ناقشناها في _مقدمة لإثباتات المعرفة الصفرية الودية_[10]. يقوم الأمر أعلاه أيضًا بإخراج _المخرجات العامة_:
هذه قائمة بجميع المخرجات العامة التي تتوافق مع شهودنا ودوائرنا. في هذه الحالة، هناك مخرجات مشتركة تتوافق مع c:33. [^21]
ماذا أثبتنا؟ نحن نعرف قيمتين سريتين a وb، وحاصل ضربهما هو 33. يوضح هذا خصائص الخصوصية التي ناقشناها في المقالة السابقة.
لاحظ أن الدليل ليس مفيدًا بمعزل عن غيره، فهو يتطلب مخرجات عامة لاحقة.
بعد ذلك، دعونا نتحقق من هذا الدليل. تشغيل:
فقط تحقق من المثال 1

يتطلب هذا التحقق من المفتاح والمخرجات العامة والإثبات. مع هذه يمكننا التحقق من الدليل. يجب أن تتم طباعة "الإثبات الذي تم التحقق منه". لاحظ أن أداة التحقق من الصحة لا تلمس أبدًا أي مدخلات خاصة.
ماذا يحدث إذا قمنا بتغيير الإخراج؟ افتح example1/target/public.json، وقم بتغيير 33 إلى 34، وقم بتشغيل الأمر أعلاه مرة أخرى.
ستلاحظ أن الدليل لم يعد يتم التحقق منه. وذلك لأن برهاننا لا يوضح أن لدينا عددين حاصل ضربهما هو 34.
تهانينا، لقد كتبت الآن برنامج ZKP الأول الخاص بك، وقمت بإعداد الثقة، وأنشأت دليلاً وتحققت منه أخيرًا!
ما الخاصيتان الرئيسيتان لـ ZKP وماذا تعنيان؟
ما هو دور المثل وما هي المدخلات التي يحتاجها؟ ماذا عن المدققين؟
اشرح الغرض من السطر c <== a * b;.
لماذا نحتاج إلى إعدادات موثوقة؟ وكيف نستخدم منتجاتها؟
الرمز: أكمل example1 حتى تقوم بإنشاء دليل والتحقق من صحته.
بالدائرة المذكورة أعلاه، نثبت أننا نعرف حاصل ضرب رقمين (سريين). يرتبط هذا ارتباطًا وثيقًا بمشكلة التحليل الأولي، والتي تعد أساس الكثير من عمليات التشفير. [^22] الفكرة هي أنه إذا كان لديك عدد كبير جدًا، فمن الصعب العثور على رقمين أوليين حاصل ضربهما يساوي هذا العدد الكبير. في المقابل، من السهل جدًا التحقق مما إذا كان منتج رقمين يساوي رقمًا آخر. [^23]
ومع ذلك، هناك مشكلة كبيرة في دائرتنا. هل تستطيع رؤيته؟
يمكننا بسهولة تغيير المدخلات إلى "1" و"33". وهذا يعني أن الرقم c يكون دائمًا حاصل ضرب 1 وc. هذا ليس مثيرًا للإعجاب، أليس كذلك؟
ما نريد فعله هو إضافة _constraint_ آخر بحيث لا يمكن أن يساوي a أو b 1. بهذه الطريقة نحن مضطرون إلى إجراء التحليل الصحيح للأعداد الصحيحة.
كيف نضيف هذا القيد وما هي التغييرات المطلوبة؟
سنستخدم المجلد example2 لإجراء هذه التغييرات. لسوء الحظ، لا يمكننا كتابة a !== 1 لأن هذا ليس قيدًا صالحًا. [^24] وهي لا تتكون من الثوابت والجمع والضرب والتحقق من المساواة. كيف نعرب عن "شيء ليس كذلك"؟
ليس من البديهي أن يكون هذا النوع من المشكلات جزءًا من فن كتابة الدوائر. يستغرق تطوير هذه المهارة وقتًا وهو خارج نطاق هذا البرنامج التعليمي الأولي؛ ولحسن الحظ، هناك العديد من الموارد الجيدة التي يمكن الرجوع إليها. [^25]
ومع ذلك، هناك بعض المصطلحات الشائعة. الفكرة الأساسية هي استخدام قالب IsZero() للتحقق مما إذا كان التعبير يساوي الصفر. ويخرج 1 للقيم الحقيقية و0 للقيم الخاطئة.
من المفيد غالبًا استخدام جدول الحقيقة [^26] لإظهار القيم المحتملة. فيما يلي جدول الحقيقة لـ IsZero():
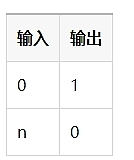
هذه كتلة بناء مفيدة حيث تم تضمينها في مكتبة Circom circomlib. هناك العديد من المكونات المفيدة الأخرى في circomlib. [^27]
يمكننا تضمينه عن طريق إنشاء مشروع npm (JavaScript) وإضافته كتبعية. في المجلد example2، قمنا بذلك بالفعل نيابةً عنك. لاستيراد الوحدات ذات الصلة، نضيف السطر التالي في أعلى example2.circom:
include "circomlib/circuits/comparators.circom";
باستخدام IsZero()، يمكننا التحقق مما إذا كان a أو b يساوي 1. قم بتعديل ملف example2.circom ليتضمن الأسطر التالية:
فقط generate_proof example2
فقط Vere_proof example2
لا يزال يُنشئ الدليل ويتحقق منه كما هو متوقع.
إذا قمنا بتغيير إدخال example2/input.json إلى 1 و33 وحاولنا تشغيل الأمر أعلاه ، سوف نرى خطأ في التأكيد. وهذا يعني أن شركة Circom لن تسمح لنا بإنشاء دليل لأن الإدخال ينتهك قيودنا.
الآن بعد أن مررنا بالعملية بأكملها مرتين، فلنرجع خطوة إلى الوراء ونرى كيف تتناسب جميع الأجزاء معًا.
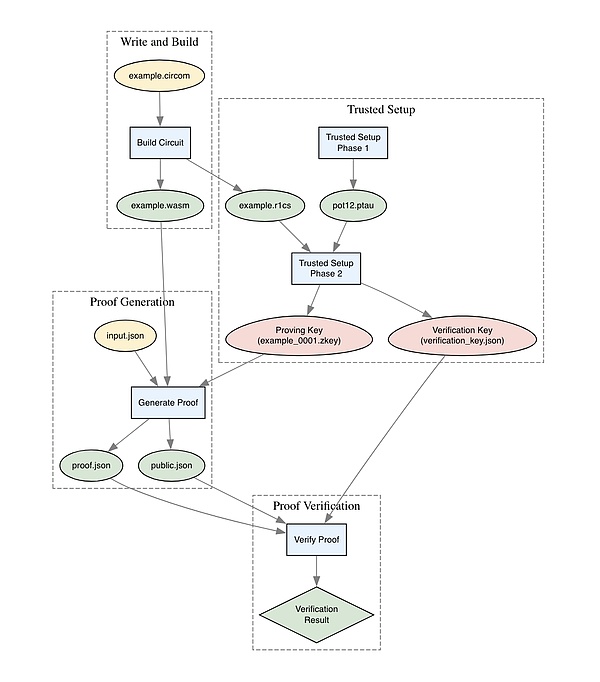
نأمل أن الأمور بدأت تتحسن أفضل قليلا واضحة. بعد ذلك، دعونا نجري بعض التحسينات لجعل دائرتنا أكثر فائدة.
لماذا يتعين علينا إجراء الجزء الثاني من example2 المرحلة بدلا من المرحلة 1؟
ما هي المشكلة الرئيسية في المثال السابق وكيف قمنا بحلها؟
الرمز: أكمل example2 حتى لا تتمكن من إنشاء دليل.
باستخدام الدائرة أعلاه، أثبتنا أننا نعرف حاصل ضرب قيمتين سريتين. وهذا وحده ليس مفيدا للغاية. في العالم الحقيقي، ما ينجح هو مخططات التوقيع الرقمي. ومن خلاله تستطيع أن تثبت للآخرين أنك كتبت رسالة معينة. كيف يمكننا استخدام ZKP لتحقيق ذلك؟ ولتحقيق ذلك، يجب علينا أولا أن نغطي بعض المفاهيم الأساسية.
الآن هو الوقت المناسب لأخذ استراحة قصيرة وتناول كوب من مشروبك المفضل.
التوقيعات الرقمية موجودة بالفعل وهي منتشرة في كل مكان في عصرنا الرقمي. ولا يمكن للإنترنت الحديث أن يعمل بدونها. عادةً، يتم تنفيذ ذلك باستخدام تشفير المفتاح العام. في تشفير المفتاح العام، لديك مفتاح خاص ومفتاح عام. المفتاح الخاص مخصص لاستخدامك فقط، بينما تتم مشاركة المفتاح العام بشكل عام ويمثل هويتك.
يتكون نظام التوقيع الرقمي من الأجزاء التالية:
إنشاء المفاتيح: إنشاء مفتاح خاص ومفتاح عام مطابق
التوقيع: أنشئ توقيعًا باستخدام المفتاح الخاص والرسالة
التحقق من التوقيع: تأكد من أن الرسالة موقعة بواسطة المفتاح العام المقابل
على الرغم من أن التفاصيل المحددة تبدو مختلفة، إلا أن البرنامج الذي كتبناه هي نفسها المذكورة أعلاه. تشترك خوارزميات توليد المفاتيح في عنصر مشترك: فهي جميعًا تستخدم _وظائف أحادية الاتجاه_، وبشكل أكثر تحديدًا _وظائف الباب المسحور_. الباب المسحور هو شيء يسهل الوقوع فيه ولكن يصعب الخروج منه (إلا إذا تمكنت من العثور على سلم مخفي) [^30].
لتشفير المفتاح العام، الإنشاء من السهل الحصول على مفتاح عام من مفتاح خاص، لكن العكس صعب للغاية. الشيء نفسه ينطبق على برنامجنا السابق. إذا كان الرقمان السريان عبارة عن أعداد أولية كبيرة جدًا، فسيكون من الصعب جدًا تحويل هذا المنتج مرة أخرى إلى قيمته الأصلية. غالبًا ما يستخدم التشفير الحديث بالمفتاح العام تشفير المنحنى الإهليلجي تحت الغطاء.
تقليديًا، يتطلب إنشاء بروتوكولات التشفير مثل أنظمة التوقيع الرقمي هذه الكثير من العمل ويتطلب التوصل إلى بروتوكول محدد يتضمن بعض الرياضيات الذكية. نحن لا نريد أن نفعل هذا. بدلاً من ذلك، نريد كتابة برنامج باستخدام ZKP يحقق نفس النتيجة.
بدلاً من ذلك: [^31]

نريد فقط أن نكتب برنامجًا يُنشئ الدليل الذي نريده، ثم يتحقق من هذا الدليل.
بدلاً من استخدام تشفير المنحنى الناقص، سنستخدم أداتين أبسط: _وظائف التجزئة_ و_الالتزامات_.
وظيفة التجزئة هي أيضًا وظيفة أحادية الاتجاه. على سبيل المثال، من سطر الأوامر، يمكننا استخدام وظيفة التجزئة SHA-256 مثل هذا:
الالتزام = hash(some_secret)
= hash(some_secret, الرسالة)
قد تكون لديك بعض الأسئلة في هذا الوقت. دعنا نتناول بعض الأسئلة التي قد تدور في ذهنك.
أولاً، لماذا يعمل هذا ولماذا نحتاج إلى ZKP؟ عندما يتحقق شخص ما من الدليل، يكون لديه فقط إمكانية الوصول إلى الالتزام والرسالة والتوقيع. ولا توجد طريقة مباشرة للتحقق من مطابقة الوعد للسر دون كشف السر. في هذه الحالة، نحن ببساطة "نكشف" السر عند إنشاء الدليل، لذلك يظل سرنا آمنًا.
ثانيًا، لماذا يتم استخدام وظائف التجزئة والالتزامات هذه داخل ZKP بدلاً من تشفير المفتاح العام؟ يمكنك تمامًا استخدام تشفير المفتاح العام داخل ZKP، وهناك أسباب مشروعة للقيام بذلك. ومن حيث القيود، فإن تكلفة تنفيذها أعلى بكثير من الحلول المذكورة أعلاه. وهذا يجعلها أبطأ وأكثر تعقيدًا مما سبق. كما سنرى في القسم التالي، فإن اختيار وظيفة التجزئة مهم جدًا.
أخيرًا، لماذا نستخدم ZKP عندما يكون لدينا بالفعل تشفير المفتاح العام؟ في هذا المثال البسيط، ليست هناك حاجة لاستخدام ZKP. ومع ذلك، فهو بمثابة لبنة بناء لتطبيقات أكثر إثارة للاهتمام، مثل مثال توقيع المجموعة المذكور في بداية هذه المقالة. ففي النهاية، نريد تشفيرًا مبرمجًا.
هذا كثير! ولحسن الحظ أننا تجاوزنا الحدبة. لنبدأ بالترميز. لا تقلق إذا لم تفهم ما ورد أعلاه بشكل كامل في البداية. يستغرق الأمر بعض الوقت للتعود على طريقة التفكير هذه.
سنبدأ العمل من الدليل example3.
لتنفيذ التوقيع الرقمي، أول شيء يتعين علينا القيام به هو إنشاء مفتاحنا. تتوافق هذه مع المفاتيح الخاصة والعامة في تشفير المفتاح العام. نظرًا لأن السر يتوافق مع هوية (أنت، جهة التصديق)، فسنسميه identity_secret وidentity_commitment على التوالي. معًا يشكلون زوجًا هوية.
ستعمل هذه كمدخلات للدائرة لاستخدامها مع الرسالة التي نريد التوقيع عليها. كمخرجات عامة سيكون لدينا التوقيعات والالتزامات والرسائل. سيسمح هذا لشخص ما بالتحقق من صحة التوقيع بالفعل.
نظرًا لأننا نحتاج إلى أزواج هوية كمدخلات للدائرة، فسوف نقوم بتوليدها بشكل منفصل: فقط generator_identity
سينتج عن ذلك شيئًا مشابهًا لما يلي:< /p> p>
include "circomlib/circuits/poseidon .circom" ;
يتم استخدام قالب تجزئة Poseidon على النحو التالي:
المكون الرئيسي {public [ ident_commitment, message]} = SignMessage();
افتراضيًا، جميع المدخلات إلى دائرتنا خاصة. بهذا، نضع علامة صراحة على identity_commitment وmessage على أنهما عامان. وهذا يعني أنها سوف تصبح جزءا من الناتج العام.
مع هذه المعلومات، يجب أن تكون لديك المعرفة الكافية لإكمال دائرة example3.circom. إذا كنت لا تزال عالقًا، يمكنك الرجوع إلى example3-solution.circom للحصول على الكود الكامل.
كما كان من قبل، يجب علينا بناء الدائرة وتشغيل المرحلة الثانية من الإعداد الموثوق:
{
"identity_secret": "21879[...]1709",
; "identity_commitment": "48269[...]7915",
"الرسالة": "42"< br >
لا تتردد في تغيير زوج الهوية إلى زوج قمت بإنشائه باستخدام فقط generator_identity بشكل صحيح . بعد كل شيء، تريد أن تبقي هويتك سرا لنفسك!
قد تلاحظ أن الرسالة مجرد رقم ("42") مقتبس كسلسلة. لسوء الحظ، نظرًا للطريقة التي تعمل بها القيود رياضيًا (باستخدام الجبر الخطي والدوائر الحسابية)، يمكننا فقط استخدام الأرقام وليس السلاسل. العمليات الوحيدة التي تدعمها الدائرة داخليًا هي العمليات الحسابية الأساسية مثل الجمع والضرب. [^37]
يمكننا الآن إنشاء دليل والتحقق منه:
["48968[...]5499", "48269[...]7915", " 42"]
يتوافق هذا مع التوقيعات والوعود والرسائل على التوالي.
دعونا نرى كيف يمكن أن تسوء الأمور إذا لم نكن حذرين. [^38]
أولاً، ماذا يحدث إذا قمنا بتغيير وعد الهوية إلى شيء عشوائي في input.json؟ ستلاحظ أننا لا نستطيع إعادة إنتاج الدليل. وذلك لأننا نتحقق أيضًا من التزام الهوية داخل الدائرة. الحفاظ على سرية الهوية والعلاقة بين الالتزام أمر بالغ الأهمية.
ثانيًا، ماذا يحدث إذا لم نقم بتضمين الرسالة في الإخراج؟ لقد حصلنا على دليل، وتم التحقق منه. لكن الرسالة يمكن أن تكون _أي شيء_، لذا فهي لا تثبت فعليًا أنك أرسلت رسالة معينة. وبالمثل، ماذا يحدث إذا لم ندرج الالتزام بالهوية في المخرجات العامة؟ هذا يعني أن التزام الهوية يمكن أن يكون أي شيء، لذلك لا نعرف فعليًا من قام بالتوقيع على الرسالة.
كتمرين فكري، فكر في ما سيحدث إذا حذفنا أيًا من هذين القيدين الرئيسيين:
identity_commitment === الهويةHasher.out
التوقيع <== التوقيعHasher.out
تهانينا، الآن أنت تعرف كيفية برمجة التشفير! [^39]
ما هي المكونات الثلاثة لنظام التوقيع الرقمي؟
ما هو الغرض من استخدام "وظيفة التجزئة الصديقة لـ ZK" مثل بوسيدون؟
ما هو الالتزام؟ كيف يمكننا استخدامها لمخططات التوقيع الرقمي؟
لماذا نضع علامة على التزامات الهوية ورسائلها على أنها عامة؟
لماذا نحتاج إلى الالتزام بالهوية وقيود التوقيع؟
الرمز: أكمل example3 حتى تقوم بإنشاء دليل والتحقق منه.
باستخدام نظام التوقيع الرقمي أعلاه وبعض التقنيات التي رأيناها في المقالة، لديك القدرة على تنفيذ ما ذكر في بداية المقالة جميع الأدوات الخاصة بنظام توقيع المجموعة. [^40]
يوجد رمز الهيكل العظمي في example4. ما عليك سوى 5-10 أسطر من التعليمات البرمجية. بناء الجملة الجديد الوحيد هو حلقة for، والتي تعمل بنفس الطريقة كما في معظم اللغات الأخرى. [^41].
ستسمح لك هذه الدائرة بما يلي:
توقيع رسالة
ولكن لا تكشف عن أي منهم
يمكنك التفكير في الأمر على أنه لغز. الفكرة الرئيسية تتلخص بشكل أساسي في التعبير الحسابي. إذا استطعت، حاول حلها على الورق. إذا واجهتك مشكلة، يمكنك مراجعة الحل كما كان من قبل.
أخيرًا، إذا كنت تريد بعض التحدي الإضافي، فإليك بعض طرق التوسيع:
السماح داخل المجموعات بأكبر عدد ممكن من الأشخاص كما تريد
نفذ دائرة كشف جديدة لإثبات أنك وقعت على رسالة معينة
تنفيذ دائرة رفض جديدة تثبت أنك لم توقع على رسالة معينة
إن إنشاء مثل هذا البروتوكول التشفيري باستخدام الأدوات الكلاسيكية سيكون بمثابة الحل الأمثل مهمة ضخمة تتطلب الكثير من الخبرة. [^42] باستخدام ZKP، يمكنك أن تصبح منتجًا وخطيرًا في فترة ما بعد الظهر، حيث تتعامل مع هذه المشكلات كمهام برمجية. وهذا مجرد غيض من فيض لما يمكننا القيام به.
ما الفرق بين توقيع المجموعة والتوقيع العادي؟ كيف يمكن استخدامها؟
هذه الأسئلة اختيارية وتتطلب المزيد من الجهد.
اكتشف كيفية تنفيذ IsZero().
الرمز: أكمل نظام توقيع المجموعة أعلاه (راجع مثال4).
الكود: توسيع مثال توقيع المجموعة أعلاه: السماح لمزيد من الأشخاص وتنفيذ دوائر كشف و/أو رفض.
كيف يمكنك تصميم نظام "ZK ID" لإثبات أن عمرك يزيد عن 18 عامًا؟ ما هي الخصائص الأخرى التي قد ترغب في إثباتها؟ وعلى مستوى عال، كيف يمكنك تنفيذه وما هي التحديات التي تراها؟ دراسة الحلول الحالية لفهم كيفية تنفيذها بشكل أفضل.
بالنسبة لسلاسل الكتل العامة مثل Ethereum، تُستخدم الطبقة الثانية (L2) أحيانًا للسماح بإجراء معاملات أسرع وأرخص وأكثر. على مستوى عالٍ، كيف يمكنك تصميم L2 باستخدام ZKP؟ اشرح بعض التحديات التي تراها. دراسة الحلول الحالية لفهم كيفية تنفيذها بشكل أفضل. ## الخلاصة
في هذه المقدمة لهذا البرنامج التعليمي، أصبحنا على دراية بكيفية كتابة وتعديل إثباتات المعرفة الصفرية الأساسية (ZKPs) من البداية. قمنا بإعداد بيئة البرمجة الخاصة بنا وكتبنا دائرة أساسية. ثم قمنا بإعداد الثقة وإنشاء الدليل والتحقق منه. لقد حددنا بعض المشكلات وقمنا بتحسين الدائرة، مع التأكد من اختبار التغييرات التي أجريناها. بعد ذلك، قمنا بتنفيذ نظام التوقيع الرقمي الأساسي باستخدام وظائف التجزئة والوعود.
لقد تعلمنا أيضًا ما يكفي من المهارات والأدوات التي تمكننا من تنفيذ التوقيعات الجماعية، وهو أمر يصعب تحقيقه بدون إثباتات المعرفة الصفرية.
آمل أن يكون لديك نموذج عقلي أفضل لما تتضمنه كتابة إثباتات المعرفة الصفرية، وفهمًا أفضل لدورة التحرير والتشغيل والتصحيح في الممارسة العملية. سيوفر هذا أساسًا جيدًا لأي برامج أخرى لإثبات المعرفة الصفرية قد تكتبها في المستقبل، بغض النظر عن مجموعة التكنولوجيا التي ستستخدمها في النهاية.
شكرًا لهانو كورنيليوس، ومارك كولبروج، وميشيل لاي، ولينيلسونجر، وتشيه-تشينغ ليانغ على قراءة المسودات وتقديم التعليقات.
مؤتمر بورباكي 1938 - غير معروف، ملكية عامة، عبر Wikimedia[11]
حمار هارتمان الوحشي - ج. هوبر، CC BY-SA 2.0، عبر Wikimedia [12]
Trapdoor Spider - PS Foresman، المجال العام، عبر [Wikimedia](https://commons.wikimedia.org/wiki) /File:Trapdoor_(PSF\ "Wikimedia").png)
Kingsley Lockbox - PS Foresman، المجال العام، عبر Wikimedia[ 13]
المواد المرجعية
[1] مترجم الذكاء الاصطناعي: https://learnblockchain.cn/people/19584
[2] فريق الترجمة: https://learnblockchain.cn/people/412
[3] learnblockchain.cn/article…: https://learnblockchain.cn/article/9178
[4] مقدمة ودية للمعرفة الصفرية: https://learnblockchain.cn/article/6184
[5] مستودع git: https://github.com/oskarth/zkintro-tutorial
< تمتد نمط = "font-size: 14px؛">[6]مستودع git: https://github.com/oskarth/zkintro-tutorial
[7]هنا: https://docs.circom.io/getting-started/installation/
[8]zkrepl.dev: https://zkrepl. dev/
[9]المستند الرسمي: https ://docs.circom.io/circom-language/signals/
[10]مقدمة ودية لإثبات المعرفة الصفرية: https://learnblockchain.cn/article/6184
[11]ويكيميديا: https://commons.wikimedia.org/wiki/File:Bourbaki_congress1938.png
[12]ويكيميديا: https://commons. wikimedia .org/wiki/File:Hartmann_zebras_hobatereS.jpg
[ 13 ]ويكيميديا: https://commons.wikimedia.org/wiki/File:Kingsley_lockbox.jpg
< تمتد نمط = "font-size: 14px؛">[14]مترجم الذكاء الاصطناعي: https://learnblockchain.cn/people/19584
[15]هنا: https://github.com/lbc-team/Pioneer/blob/master/translations/9178. md
[16]^2]: راجع [ الأوراق الفيدرالية (ويكيبيديا): https://en.wikipedia.org/wiki/The_Federalist_Papers#Authorship
[17]^3]: راجع [بورباكي (ويكيبيديا): https://en.wikipedia.org/wiki/Nicolas_Bourbaki#Membership
[18]^8]: يسمح هذا بكتابة القيود تمامًا صعبة، كما يمكنك أن تتخيل. لمزيد من التفاصيل حول القيود في Circom، راجع [ https://docs.circom.io/circom-language/constraint-generation/:https://docs.circom.io/circom-language/constraint -generation/
[19]^12]: القيد الخطي يعني أنه يمكن التعبير عنها كمجموعة خطية عن طريق الجمع فقط. وهذا يعادل الضرب باستخدام الثوابت. الشيء الرئيسي الذي يجب ملاحظته هو أن القيود الخطية أبسط من القيود غير الخطية. لمزيد من التفاصيل، راجع [إنشاء القيد: https://docs.circom.io/circom-language/constraint-generation/
[20] الدوائر الحسابية: https://docs.circom.io/background/background/#arithmetic-circuits< /span>
[21]^13]: من الناحية الرياضية، ما قمنا به هو تأكد من أن المعادلةAz * Bz = Cz تم تأسيسه حيثZ=(W,x,1). أ, ب و C عبارة عن مصفوفة، W شاهد (إدخال خاص)، x هو إدخال/إخراج عام. على الرغم من أنه من المفيد معرفة ذلك، إلا أنه ليس من الضروري فهمه عند كتابة الدائرة. لمزيد من التفاصيل، راجع [نظام القيد Rank-1: https://docs.circom.io/background/background/#rank-1-constraint-system< p style="text-align: left;">[22]^15]: كما في مقالة المقدمة الودية كما هو مذكور في ، هناك بودكاست جيد لشخص عادي حول الحفل الذي أقامته Zcash في عام 2016، والذي يمكنك مشاهدته [هنا: https://radiolab.org/podcast/ceremony< p style="text-align: left;">[23]^17]: نحن نسميه نموذج الثقة 1 خارج N. هناك العديد من نماذج الثقة الأخرى؛ ولعل أكثر نماذج الثقة التي تعرفها هو حكم الأغلبية، حيث تثق في قدرة أغلبية الأشخاص على اتخاذ القرار الصحيح. هذه هي الطريقة الأساسية التي تعمل بها الديمقراطية وتصويت الأغلبية. [↩: #user-content-fnref-17
[24]^22]: تُعرف أيضًا باسم _فرضية صعوبة التشفير_. راجع [افتراضات الصلابة الحسابية (ويكيبيديا): https://en.wikipedia.org/wiki/Computational_hardness_assumption#Common_cryptographic_hardness_assumptions
[25]^23]: لمزيد من المعلومات، راجع [https://en.wikipedia.org/wiki/Integer_factorization: https:/ /en.wikipedia.org/wiki/Integer_factorization
[26 ]^24]: على الرغم من أنه يمكننا إضافة _asserts_، إلا أنها ليست في الواقع قيودًا وتستخدم فقط لتنظيف المدخلات. لمعرفة كيفية عمل ذلك، راجع [https://docs.circom.io/circom-language/code-quality/code-assertion/:https://docs.circom.io/circom-language/code-quality /تأكيد الكود/
[27]https:/ / www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions: https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions
[28]^25]: هذا المورد المقدم من 0xPARC ممتاز إذا أردت لمعرفة المزيد عن فن الكتابة (Circom) الدوائر: [https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/:https://learn.0xparc. org/materials/circom/learning-group-1/circom-1/
[29]^26]: بسبب طبيعة قيود الكتابة، يحدث هذا الموقف بشكل متكرر. راجع [https://en.wikipedia.org/wiki/Truth_table: https://en.wikipedia.org/wiki/Truth_table
[30]^27]: لمزيد من المعلومات حول circomlib، راجع [https://github.com/iden3/ circomlib: < em>https://github.com/iden3/circomlib
[31]^28]: راجع [https://github.com/iden3/circomlib/blob/master/circuits/comparators.circom: https://github.com/iden3 /circomlib/blob /master/circuits/comparators.circom
[32]^ 29]: غالبًا ما يشارك الأشخاص هذه العناصر بين المشاريعptau ملف لتحسين الأمان. لمزيد من المعلومات، راجع [https://github.com/privacy-scaling-explorations/perpetualpowersoftau: https://github.com/privacy-scaling-explorations/perpetualpowersoftau< / p>
[33]https://github.com/iden3/snarkjs: https:/ / github.com/iden3/snarkjs
[34]^ 30 ]: يمثل السلم هنا نوعًا من القيمة التي تسمح لنا بالمضي قدمًا في الاتجاه المعاكس "الصعب". طريقة أخرى للتفكير في الأمر هي بمثابة قفل. يمكنك قفله بسهولة، ولكن من الصعب فتحه إلا إذا كان لديك مفتاح. وظيفة الباب المسحور لها أيضًا تعريف أكثر رسمية، راجع [https://en.wikipedia.org/wiki/Trapdoor_function: https://en.wikipedia.org/wiki/Trapdoor_function
[35]^31]: لقطة شاشة من ويكيبيديا. راجع [ECDSA (ويكيبيديا): https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Signature_verification_algorithm
[36]^38]: في أنظمة التوقيع الرقمي في العالم الحقيقي، عند تبادل رسائل متعددة، قد نرغب أيضًا في تقديم رقم عشوائي مشفر. وذلك لتجنب هجمات الإعادة، حيث يمكن لشخص ما إعادة استخدام نفس التوقيع في وقت لاحق. راجع [https://en.wikipedia.org/wiki/Replay_attack: https://en.wikipedia.org/wiki/Replay_attack
[37]^40]: إن تنفيذ توقيع المجموعة في ZKP مستوحى من 0xPARC، يرجى الاطلاع على [https://0xparc. org/blog/zk-group-sigs: https://0xparc.org/blog/zk-group-sigs
[38]^41]: راجع [https://docs.circom.io/circom-language/control-flow/: https ://docs.circom.io/circom-language/control-flow/
[39]^42]: في المقابل، تطبق الأوراق البحثية توقيعات المجموعة مثل [https://eprint.iacr.org/2015/043.pdf: https:// eprint.iacr .org/2015/043.pdf
SAFT وSAFE هي طرق تمويل بسيطة ومرنة وفعالة، ولا تستغرق سوى بضع صفحات. يتم استخدام SAFT لرفع حقوق العملة، ويتم استخدام SAFE لرفع حقوق الملكية.
 JinseFinance
JinseFinanceتتمتع شبكات الرمز المميز التي تدعمها البرامج ويديرها المجتمع بإمكانات هائلة للتأثير على الاقتصاد والمجتمع العالمي بأكمله.
 JinseFinance
JinseFinanceتطلق Golden Finance "Golden Web3.0 Daily" لتزويدك بأحدث وأسرع الألعاب وأخبار صناعة DeFi وDAO وNFT وMetaverse.
 JinseFinance
JinseFinanceجزر كايمان مقابل جزر الباهاما: كيف أثرت فضيحة FTX على كلا السلطتين القضائيتين.
 Beincrypto
Beincryptoكان صندوق التحوط المشفر المفلس يهدف في السابق إلى جمع 100 مليون دولار من NFT ، والتي قد تكون الآن أقل من مليون دولار.
 Coindesk
Coindeskنعم ، هذا صحيح. أصدر مكتب التحقيقات الفيدرالي (FBI) مؤخرًا تحذيرًا بشأن مآثر المجرمين الإلكترونيين التي تستهدف DeFi. في الواقع ، كانت منصات DeFi ...
 Bitcoinist
Bitcoinistفي مقابلة مع كوينتيليغراف ، أوضح النائب إيزولا المشهد التنظيمي للعملات المشفرة في جبل طارق واهتمامه ببيتكوين.
 Cointelegraph
Cointelegraph这位比利时议员将通过该国流行的加密货币交易平台Bit4You,将他5500欧元的月薪转换为比特币。
 Cointelegraph
Cointelegraph吉尔吉斯斯坦对加密货币交易所和挖矿业进行了监管,但是,该国没有监管加密货币流通的法律。
 Cointelegraph
Cointelegraphنظمت قيرغيزستان عمليات تبادل العملات المشفرة وصناعة التعدين ، ومع ذلك ، لا توجد قوانين تحكم تداول العملات المشفرة في البلاد.
 Cointelegraph
Cointelegraph