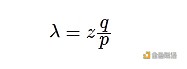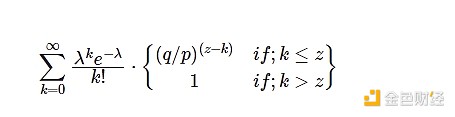Note: On October 31, 2008, Satoshi Nakamoto published the Bitcoin white paper "Bitcoin: A Peer-to-Peer Electronic Cash System" on the P2P foundation website. On the 16th anniversary of the release of the white paper, in order to reread this classic that has forever changed the financial world, Golden Finance has republished the Chinese version of the Bitcoin white paper.
Author: Satoshi Nakamoto; Translator: Li Xiaolai
Summary: A purely peer-to-peer version of the electronic cash system will allow online payments to be sent directly from one party to another without going through a financial institution. Although digital signatures provide a partial solution, if a trusted third party is still required to prevent double spending, the main advantage of electronic payments is offset. We propose a solution to solve the double spending problem using a peer-to-peer network. The peer-to-peer network will timestamp each transaction by entering the hash data of the transaction into an ever-extending hash-based proof-of-work chain, forming a record that cannot be changed unless it is completely redone. The longest chain is used to prove that events have been witnessed and their order, and that it came from the largest pool of CPU power. As long as the majority of CPU power is controlled by benign nodes - that is, they do not cooperate with nodes that are trying to attack the network - then benign nodes will generate the longest chain and outpace attackers. The network itself needs to have minimal structure. Information will be propagated on a best-effort basis, and nodes will come and go freely; but joining is always required to accept the longest proof-of-work chain as proof of everything that happened during their absence.
1. Introduction
Internet commerce relies almost entirely on financial institutions as trusted third parties to process electronic payments. While this system works well for most transactions, it is still hampered by the inherent flaws of the trust-based model. Completely irreversible transactions are not actually possible because financial institutions cannot avoid arbitration disputes. Arbitration costs increase transaction costs, which in turn limits the size of the smallest possible transaction and simply prevents many small payments. On top of this, there is an even greater cost: the system cannot provide irreversible payments for irreversible services. The possibility of reversal creates a pervasive need for trust. Merchants must be wary of their customers, and trouble them to provide more information that would otherwise be unnecessary. A certain amount of fraud is considered inevitable. These costs and payment uncertainties are avoidable when physical currency is used directly between people; however, no mechanism can make payments through a communication channel without trusting one of the parties.
What is really needed is an electronic payment system based on cryptographic proofs rather than trust, allowing any two parties to transact directly without trusting a third party. Irreversible transactions guaranteed by computational power can help sellers avoid fraud, and daily guarantee mechanisms to protect buyers are easy to implement. In this paper, we will propose a solution to double spending, using a peer-to-peer, distributed timestamp server to generate computational proofs that record each transaction in chronological order. This system is secure as long as the honest nodes in aggregate have more CPU power than a cooperating attacker.
2. Transactions
We define an electronic coin as a chain of digital signatures. When an owner hands a coin to another person, the following digital signature is appended to the end of this digital signature chain: the hash of the previous transaction, and the public key of the new owner. The recipient can verify the ownership of the digital signature chain by verifying the signature.
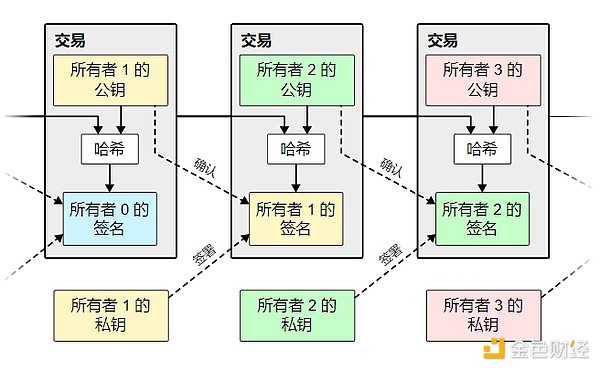
The problem with this path is that the recipient cannot verify that no one of the previous owners has double-spent. A common solution is to introduce a trusted centralized authority, or "mint", to check whether there is a double payment in each transaction. After each transaction, the coin must be returned to the mint, and the mint will issue a new coin. Furthermore, only coins issued directly by the mint can be trusted not to have been double-spent. The problem with this solution is that the fate of the entire monetary system is tied to the company that runs the mint (just like a bank), and every transaction must go through it.
We need a way for the recipient to confirm that the previous owner did not sign any previous transactions. For our purposes, only the earliest transaction counts, so we don't care about subsequent double-spend attempts. The only way to confirm that a transaction did not exist is to know all transactions. In the mint model, the mint already knows all transactions and can confirm the order of them. In order to complete the above tasks without the participation of a "trusted party", transaction records must be publicly announced 1, and then we need a system that allows participants to agree that they have received the same unique transaction history. The payee needs to prove that at the time of each transaction, most nodes can agree that it is the first to be received.
3. Timestamp Server
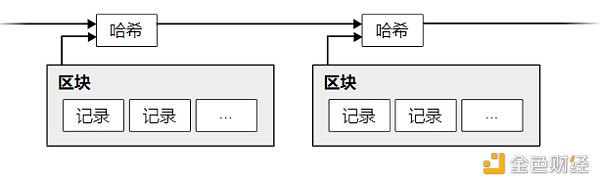
This solution starts with a timestamp server. A timestamp server works by timestamping a hash of a block of records (items) and then broadcasting the hash, just like a newspaper would do, or like a post in a Usenet newsgroup 2 3 href="https://github.com/xiaolai/bitcoin-whitepaper-chinese-translation/blob/master/Bitcoin-Whitepaper-EN-CN.md#user-content-fn-4-c578f184e4f1bbac8a6359f5f7bb8725">4 5. Obviously, the timestamp can prove that the data existed before that point in time, otherwise the hash cannot be generated. Each timestamp contains the previous timestamp in its hash, thus forming a chain; each new timestamp is added to the previous timestamp.
4. Proof-of-Work
In order to implement a peer-to-peer distributed timestamp server, we need to use a proof-of-work system like Adam Burke's HashCash6, rather than something like a newspaper or newsgroup post. Proof of work is about finding a value that, when hashed — for example, using SHA-256 — must start with a certain number of zeros. Each additional zero requirement increases the amount of work exponentially, and the work can be verified by just computing a single hash.
In our timestamp network, we implement proof of work by adding a nonce to the block until a value is found that satisfies the condition that the block's hash starts with a specified number of zeros. Once the CPU effort to calculate the result satisfies the proof of work, the block can no longer be changed without redoing all the work that went into it. As new blocks are added, changing the current block means redoing all the work that went into the blocks that followed it.
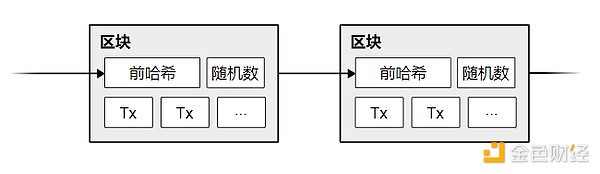
Proof of work also solves the problem of how to decide who can make decisions on behalf of the majority. If the so-called "majority" is based on "one IP address one vote", then anyone who can handle many IP addresses can be considered "majority". Proof of work is essentially "one CPU one vote". The so-called "majority decision" is represented by the longest chain, because it is the chain that has been put into the most work. If most CPU computing power is controlled by honest nodes, then the honest chain will grow the fastest, and its speed will far exceed other competing chains. In order to change a block that has already been generated, the attacker will have to re-complete the proof of work of that block and all subsequent blocks, and then catch up with and exceed the work of the honest nodes. The following text shows why the probability of a delayed attacker catching up decreases exponentially as the number of blocks increases.
To cope with the increasing overall hardware computing power and the possible changes in the number of participating nodes over time, the proof of work difficulty is determined as follows: a moving average based on the average number of blocks generated per hour. If blocks are generated too quickly, the difficulty will increase.
5. Network
The steps to run the network are as follows:
All new transactions are broadcast to all nodes;
Each node packs the new transactions into a block;
Each node starts looking for a difficult proof of work for this block;
When a block finds its proof of work, it broadcasts this block to all nodes;
Many other nodes will accept this block if and only if the following conditions are met: all transactions in it are valid and not double-spent;
The way many nodes indicate to the network that they accept this block is to use the hash of the accepted block as the hash before the new block when creating the next block.
Nodes always believe that the longest chain is the correct one and will continue to add new data to it. If two nodes simultaneously broadcast two different versions of the "next block" to the network, some nodes will receive one first, while others will receive the other first. In this case, the nodes will continue to work on the block they received first, but will also save the other branch in case the latter becomes the longest chain. When the next proof of work is found and one of the branches becomes a longer chain, this temporary disagreement will be resolved, and the nodes working on the other branch will switch to the longer chain.
New transactions do not necessarily have to be broadcast to all nodes. As long as they reach enough nodes, they will be packaged into a block soon. Block broadcasting also allows some messages to be discarded. If a node does not receive a block, then when it receives the next block, it will realize that it has missed the previous block, so it will issue a request to supplement the missing block.
6. Incentive
According to the agreement, the first transaction of each block is a special transaction that generates a new coin, which belongs to the generator of this block. This rewards nodes for supporting the network and provides a way to release coins into circulation — in a system where there is no central authority that releases those coins anyway. This steady flow of new coins into circulation is like gold miners constantly expending their resources to add gold to circulation. In our system, the resources expended are CPU time and the electricity they use.
Rewards can also come from transaction fees. If the output of a transaction is less than its input, the difference is the transaction fee, which is used to reward nodes for including the transaction in the block. Once a given number of coins have entered circulation, rewards are fully covered by transaction fees, and there is absolutely no inflation.
Rewards may also encourage nodes to stay honest. If a greedy attacker is able to gather more CPU power than all the honest nodes, he must make a choice: use that power to cheat others by stealing back the money he spent? Or use that power to generate new coins? He should be able to find that it is more cost-effective to play by the rules, which currently allow him to get more coins than all the others combined, which is obviously more cost-effective than secretly destroying the system and destroying his wealth.
7. Reclaiming Disk Space
If the most recent transaction of a coin occurred many blocks ago, then the transaction record of the coin spent before this transaction can be discarded - the purpose is to save disk space. In order to achieve this function without destroying the hash of the block, the hash of the transaction record will be included in a Merkle tree, and only the root of the tree will be included in the hash of the block. By cutting off branches, old blocks can be compressed. The internal hash does not need to be saved.
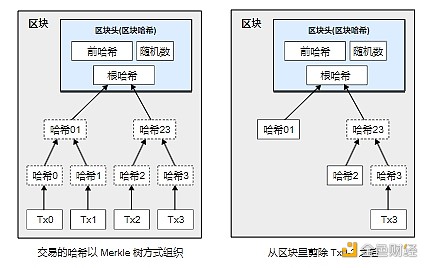
A block header without any transaction record is about 80 bytes. Assuming that one block is generated every ten minutes, 80 bytes multiplied by 6 multiplied by 24 multiplied by 365 equals 4.2M per year. As of 2008, most computers on sale have 2GB of memory, and according to Moore's Law, it will increase by 1.2 GB per year, so even if the block header must be stored in memory, it will not be a problem.
8. Simplified Payment Confirmation
It is possible to confirm payments even without running a full network node. A user only needs to have a copy of the block headers of the longest chain with proof of work — he can confirm that what he has is indeed from the longest chain by querying online nodes — and then get the branches of the Merkle tree, and then connect to the transaction when the block was timestamped. The user cannot check the transaction himself, but, by connecting to somewhere in the chain, he can see that a network node has accepted the transaction, and the blocks added later further confirm that the network has accepted the transaction.
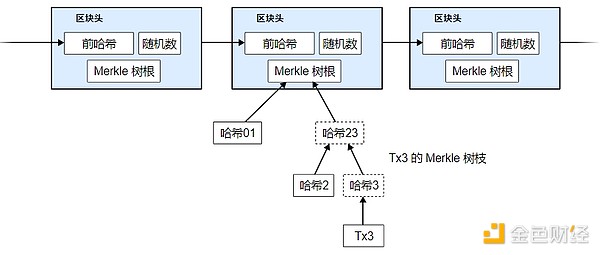
As long as honest nodes are still in control of the network, verification is reliable. However, if the network is controlled by an attacker, verification is not so reliable. Although network nodes can verify transaction records by themselves, as long as the attacker can continue to control the network, the simplified verification method may be deceived by the attacker's forged transaction records. One of the countermeasures is that the client software should accept warnings from network nodes. When the network node finds an invalid block, it will issue an alarm and pop up a notification on the user's software to inform the user to download the full block and warn the user to confirm the consistency of the transaction. Merchants with high-frequency payment and collection should still want to run their own full nodes to ensure more independent security and faster transaction confirmation.
9. Combination and division of value
Although it is possible to handle coins one by one, it is cumbersome to set up a separate record for each cent. In order to allow the division and combination of value, the transaction record contains multiple inputs and outputs. Generally, there is either a single input from a relatively large previous transaction, or many inputs from a combination of smaller amounts; at the same time, there are at most two outputs: one is the payment (to the recipient), and if necessary, the other is the change (to the sender).
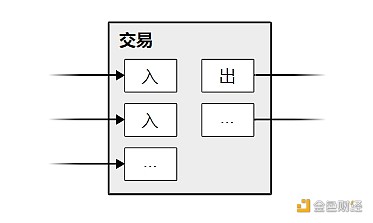
It is worth noting that "fan-out" is not a problem here - the so-called "fan-out" means that one transaction depends on several transactions, and these transactions depend on more transactions. There is never a need to extract a complete and independent copy of the history of any transaction.
10. Privacy
The traditional banking model achieves a certain degree of privacy protection by limiting others' access to information about traders and trusted third parties. The need to make all transaction records public has rejected this approach. However, maintaining privacy can be achieved by cutting off the flow of information at another point - public key anonymity. The public can see that someone transferred a certain amount of money to someone else, but no information points to a specific person. This level of information release is a bit like stock market trading, where only the time and amount of each transaction are announced, but no one knows who the two parties are.
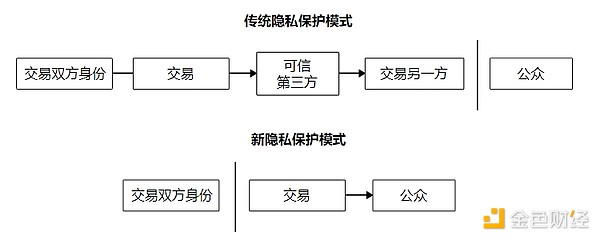
There is another layer of firewall. Traders should use a new pair of public and private keys for each transaction so that others cannot trace the transactions back to the same owner. Some multi-input transactions are still difficult to trace because those inputs must be identified as coming from the same owner. The danger is that if the owner of a public key is exposed, all other transactions related to it will be exposed.
11. Calculations
Suppose a scenario where an attacker is trying to generate an alternative chain that is faster than the honest chain. Even if he succeeds, he cannot make arbitrary changes to the system, that is, he cannot create value out of thin air, nor can he obtain money that never belonged to him. Network nodes will not treat an invalid transaction as a payment, and honest nodes will never accept a block containing such a payment. The attacker can only modify his own transactions at most and try to get back the money he has spent.
The competition between the honest chain and the attacker can be described by a binomial random walk. The success event is that a new block has just been added to the honest chain, which increases its advantage by ; and the failure event is that a new block has just been added to the honest chain, which increases its advantage by ; The failure event is that a new block has just been added to the attacker's chain, which reduces the advantage of the honest chain by 1. The probability that the attacker can catch up from behind is similar to the gambler's ruin problem. Suppose a gambler with unlimited chips starts from a deficit and is allowed to gamble unlimited times, with the goal of filling the existing deficit. We can calculate the probability that he will eventually fill the gap, that is, the probability that the attacker will catch up with the honest chain, as follows:

Since we have assumed ,q Since the number of blocks that the attacker needs to catch up increases, his chance of success will decrease exponentially. When the odds are against him, if the attacker does not get lucky and take a big step forward at the beginning, his chance of winning will be eliminated as he falls further behind.
Now consider how long the recipient of a new transaction needs to wait to be fully certain that the sender cannot change the transaction. Let's assume that the sender is an attacker who intends to make the recipient believe for a while that he has paid the counterparty, and then transfer the money back to him. When this happens, the recipient is of course warned, but the sender hopes that by then the matter is done.
The recipient generates a new public-private key pair and then tells the sender the public key shortly before signing. This prevents a situation where the sender prepares a block on one chain in advance by running calculations in succession, and with enough luck gets ahead enough to execute the transaction until then. Once the payment has been sent, the dishonest sender secretly starts working on another parallel chain, trying to insert a reverse version of the transaction into it.
The recipient waits until the transaction is included in a block, and z blocks have been added to it since then. He does not know how the attacker is progressing, but can assume that the average time it takes for honest blocks to be generated in each block; the attacker's potential progress follows a Poisson distribution with an expected value of:
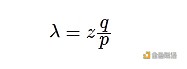
To calculate the probability that the attacker can still catch up, we need to multiply the probability density of the Passon distribution of the number of blocks the attacker needs to catch up by the probability of catching up after falling behind by that number of blocks:
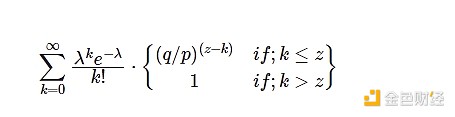
Convert to C language program...
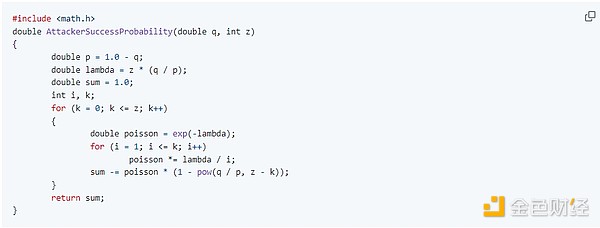
Get some results, we can see that the probability decreases exponentially with the increase of z:

If P is less than 0.1%…

12. Conclusion
We proposed an electronic transaction system that does not rely on trust; the starting point is a common coin framework using digital signatures, which, while providing robust ownership control, cannot avoid double spending. To solve this problem, we propose a peer-to-peer network that uses proof-of-work to record a public history of transactions, so that as long as honest nodes can control a majority of CPU power, it is impossible for an attacker to successfully tamper with the system based on computing power alone. The robustness of this network lies in its unstructured simplicity. Nodes can work simultaneously and instantaneously with little coordination. They don't even need to be identified, because the path of a message does not depend on a specific end point; the message just needs to be propagated on a best-effort basis. Nodes are free to come and go, and when they rejoin, they only need to accept the proof-of-work chain as proof of everything that happened while they were offline. They vote with their CPU power, expressing their acceptance or rejection of valid transactions by continuously adding new valid blocks to the chain and rejecting invalid blocks. Any necessary rules and rewards can be enforced through this consensus mechanism.
References
b-money Dai Wei (1998-11-01) http://www.weidai.com/bmoney.txt
-
Design of a secure timestamping service with minimal trust requirements Henri Massias, Xavier Serret-Avila, Jean-Jacques Quisquater 20th Symposium on Information Theory in the Benelux (1999-05) http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.13.6228
How to time-stamp a digital document Stuart Haber, W.Scott Stornetta Journal of Cryptology (1991) https://doi.org/cwwxd4 DOI: 10.1007/bf00196791 liability of Digital Time-Stamping Dave Bayer, Stuart Haber, W. Scott Stornetta Sequences II (1993) https://doi.org/bn4rpx DOI: 10.1007/978-1-4613-9323-8_24
Secure names for bit-stringsStuart Haber, W. Scott Stornetta Proceedings of the 4th ACM conference on Computer and communications security - CCS ’97(1997) https://doi.org/dtnrf6 DOI: 10.1145/266420.266430
Hashcash - A Denial of Service Counter-Measure Adam Back (2002-08-01) https://doi.org/bmvbd6 DOI: 10.1109/sp.1980.10006
An Introduction to Probability Theory and its Applications William Feller John Wiley & Sons (1957) https://archive.org/details/AnIntroductionToProbabilityTheoryAndItsApplicationsVolume1
 Joy
Joy