Cooperative Game Theory: Nash Bargaining Theory and Bitcoin

Author: Jon Gulson, Bitcoin Magazine; Compiler: Songxue, Golden Finance

“I think economics is a bit like accounting - you know, it doesn’t involve any morality. You can study welfare economics To learn, try to think about some human values, or you can look at variations." — John F. Nash Jr., University of Scranton, November 2011.

This quote from John Forbes Nash Jr. comes from a lecture he gave on "Ideal Money and the Motivation of Savings and Thrift," which was just before his first paper on game theory. It has been 61 years since the publication of the paper "The Bargaining Problem" (1950).

The Bargaining Problem is important because it is considered one of the first examples of the introduction of the axiomatic method in the social sciences. Nash presented "The Bargain Problem" as a new treatment of classical economic problems - treating it as a non-zero-sum, two-player game in which he made some general assumptions and "certain idealizations", in order to find the value for the game.

The genetic lineage from "The Bargain Problem" to Nash's later research on ideal money was established, and in "The Bargain Problem" Nash commented on the utility of money:

"The problem may assume a particularly simple form when the bargainers have a common medium of exchange. In many cases the monetary equivalent of the commodity will serve as a satisfactory approximation of the utility function." John F. Nash Jr., The Bargaining Problem (1950).

Nash's Bargain explores how a dollar is divided equitably among the participants in a financial transaction or contract. Each party has a set of interests and preferences, and an agreement must be reached, otherwise both parties will end up dead. Nothing gained. The axioms introduced for Nash transactions then define a unique solution.

Nash Equilibrium and Nash Bargaining

In "The Essential John Nash" (2007), Harold Kuhn describes Nash's subsequent "Non-Cooperative Games" (1950 ) paper, and what came to be known as the theory of Nash equilibria, which he called a "clumsy, but completely original application" of Brouwer's fixed point theorem. However, it was Nash's concept of equilibrium that gave him public attention through the Nobel Prize in Economic Science. Later, Nash's life was adapted into the Hollywood movie "A Beautiful Mind."

In "Non-Cooperative Games", Nash's theory is based on "the absence of alliances, which assumes that each participant acts independently, without cooperation or communication with anyone else." In Adam Curtis's television documentary The Trap (2007), Nash described his theory of equilibrium as social adjustment:

"...the kind of equilibrium used is, What I do fits perfectly with what you do, and what you do or anyone else does fits perfectly with what I do or everyone else does. They are looking to optimize independently, just like poker Poker players alike.” John F. Nash Jr., The Trap (2007, Adam Curtis), F*ck You, Buddy.

The difference between Nash equilibrium and Nash bargaining is that axiomatic bargaining (or reaching a Nash bargain) does not assume equilibrium. Instead, it states the desired properties of the solution. Nash bargaining is considered cooperative game theory because of its non-zero-sum nature and the existence of contracts. Nash extended the axiomatic treatment of the bargaining problem in Two-Person Cooperative Games (1953) by introducing a threat approach in which a referee enforces the contract - in which Think of "strategy" as having no special qualities and focusing more on determining the formal representation of the game.

Ideal Money and Asymptotic Ideal Money

At the turn of the century, John Nash began writing and teaching An evolving thesis called Ideal Money. The theory went through different iterations over the years, but Nash defined it as money that is inherently immune to inflation or inflationary corruption. Nash was not so critical of economists or Keynes as a person, but of so-called Keynesian psychology; which Nash saw as a Machiavellian scheme to perpetuate inflation and currency devaluation. Nash argued that if central banks were to target inflation, they should target “so-called inflation” at zero:

“What’s really respectable is that inflation Inflation should not have arbitrary or capricious patterns, but how to define a suitable and ideal form of stabilization of the value of money?" John F. Nash Jr., "Ideal Money and Asymptotically Ideal Money" (2010).

In "Ideal Money," Nash returned to the axiomatic approach he first established in his early days of game theory. Ideal Money thus offers a critique of Keynesian macroeconomics:

"Thus I consider Keynesian macroeconomics to be comparable to scientific research in the field of mathematics using an inadequate set of axioms." John ·F. Nash Jr., "Ideal Money and Asymptotic Ideal Money" (2008).

Nash defines the missing axiom:

“The missing axiom is the accepted axiom that money put on the market by a central authority should be treated so as to maintain its value over a long period of time. Stable Value." John F. Nash Jr., Ideal Money and Asymptotically Ideal Money (2008).

In the 2002 Southern Magazine edition of Ideal Money, Nash realized that ideal money would not be completely immune to inflation (or be too "good") because it would have problems in circulation, and May be exploited by a party wishing to store wealth safely. Nash then introduced a stable and constant inflation rate (or asymptote) that could be added to lending contracts.

Indeed, Nash described the purpose of ideal money in the context of cooperative games and microeconomics:

“One thing we did not consider when we first thought about ideal money, and only realized later. The concept is that the comparative quality of money used in an economic society is critical to the accuracy of contracts as an indicator of the quality of future contract performance." John F. Nash Jr., "Ideal Money and Asymptotically Ideal Money" ( 2008).

Bitcoin as an axiomatic design

If Nash's view of economics is that it lacks any direct moral concepts - values, assumptions, axioms, variations or idealizations that can be introduced to determine a non-zero-sum or deterministic game that provides well-being for all participants - then it is worth considering whether these axioms exist in Bit currency system, given that Nash, along with Satoshi Nakamoto, were critical of the arbitrary (or indeterminate) nature of centrally managed currencies.

Pareto efficiency

Pareto efficiency in terms of the cumulative supply density and distribution of Bitcoin The existence of is probably the most demonstrative of Nash's bargaining axioms (see illustration): most Bitcoins were mined early in Bitcoin's history (roughly following the Pareto 80/20 power law).

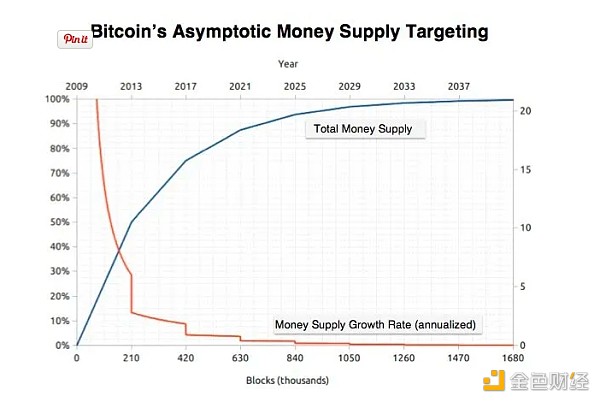
1. Incorrect scale Invariance

Scale invariance exists through a difficulty adjustment mechanism that makes the Bitcoin supply "stable and constant" (a term used by both Nash and Satoshi Nakamoto). No matter how popular or unpopular Bitcoin becomes, scale invariance should mean that participants can form realistic expectations about the value of Bitcoin, and their underlying preferences should not change in this regard. Bitcoin’s internal divisibility also means that on shorter or immediate time frames, a coin’s expressed value (whether in dollars or other currencies) should not matter — just like room temperature can be expressed in degrees Celsius or Fahrenheit without It affects the actual temperature. These differences only become apparent in transactions over longer periods of time or across time.

The adjustment mechanism also keeps the total supply of Bitcoin below 21 million, which is set this way as a side effect of the system's data structure.

2. Symmetry

Nash’s symmetry axiom exists in the anonymity and decentralization of the Bitcoin network, achieved by eliminating the need to prove first-person identity when participating in the core or main network. Anonymity (a term introduced by Nash in The Bargaining Problem). This means there is no centralized or trusted body responsible for minting Bitcoins, an "amnestyer" in Nash's words. Related to Nash bargaining, if two players have the same utility function and are therefore indistinguishable, then they should receive the same amount. Alvin Ross (1977) concluded that a player's label does not matter: "If switching a player's label does not change the bargaining problem, then it should not change the solution."

3. Irrelevant Substitutions Independence of Alternatives (IIA)

Finally, there is Nash's most controversial bargaining axiom: the independence of irrelevant alternatives. Simply put, this means that adding a third party (or non-winning candidate) to an election between two players should not change the outcome of the election (the third party becomes irrelevant). If peer-to-peer refers to a two-player game, where the Bitcoin network acts as a third-party arbiter or referee over the "game", and the software is designed as a set of values ​​or axioms, then there may be something irrelevant in Bitcoin's proof-of-work Independence of alternatives. This comes into the context of social group preferences: the proof of work says it solves the problem of determining representation in majority decisions, and Nash's bargaining axioms (both in the Bargaining Problem and the Two-Person Cooperative Game) explicitly solve The problem of formal representation in games.

Characteristics and benefits of cooperation

Generally speaking, cooperative games require three conditions:

1. Reduce the number of participants, namely two players.

2. Contract, where participants can agree on a reasonable joint action plan, which can be enforced by external agencies such as courts.

3. Participants are able to communicate and collaborate on the basis of trusted information and have full access to the structure of the game (such as the Bitcoin blockchain).

In Non-zero-sum games and monetary preferences, John Nash considers how money promotes transferable utility through "lubrication" and makes the following observation:

"In In game theory, there is often the concept of 'payoff' if the game is more than just winning or losing (or a game of winning, losing or drawing). The game may involve all actions being performed simultaneously, so that the utility measure used to define payoffs can Adopt any actual money having good divisibility and measurability properties at the relevant moment." John F. Nash Jr., Ideal Money and the Motives of Savings and Frugality (2011).

Benefits of cooperation include reduced need for mediation or dispute resolution as contracts and agreements become more trustworthy; reduced border friction in trade; non-zero sum outcomes (win-win bargaining or welfare economics) ; more intuitive, informal decision-making; and the possibility of alliance formation, which was the context of world empire that John Nash ultimately defined. The latter makes solving difficult problems such as zero net emissions (or any other problem requiring multilateral coordination) more realistic. Nash compared his ideal money proposal to an old-fashioned sovereign currency:

“Any version of an ideal money (one that is essentially immune to inflation) would necessarily resemble one that provides a practical medium for transactions. Classical 'sovereign' or 'lord.'" John F. Nash Jr., Ideal Money and the Motives of Savings and Frugality (2011).

In 2011, Nash also thought about a "game" of "contract signing", as if the ideal currency was the contract: There is another player, and this player is the monarch, who provides the expression of the contract in the form of money." John F. Nash Jr., Ideal Money and the Motives of Savings and Frugality (2011 ).