Vitalik: How to align with Ethereum
"Ethereum alignment" includes value alignment, technical alignment, and economic alignment.
 JinseFinance
JinseFinance
Compiled by: Kate, Mars Finance
Over the past two years, STARKs have become a critical and irreplaceable technology for efficiently making easily verifiable cryptographic proofs of very complex statements (e.g., proving that an Ethereum block is valid).
One of the key reasons for this is field size: SNARKs based on elliptic curves require you to work on 256-bit integers to be secure enough, while STARKs allow you to use smaller field sizes with greater efficiency: first the Goldilocks field (64-bit integers), then Mersenne31 and BabyBear (both 31 bits). Due to these efficiency gains, Plonky2, which uses Goldilocks, is hundreds of times faster than its predecessors at proving many kinds of computations.
A natural question is: Can we take this trend to its logical conclusion and build proof systems that run faster by operating directly on zeros and ones? This is exactly what Binius attempts to do, using a number of mathematical tricks that make it very different from SNARKs and STARKs from three years ago. This post describes why small fields make proof generation more efficient, why binary fields are uniquely powerful, and the tricks Binius uses to make proofs on binary fields so efficient.

△ Binius. By the end of this post, you should be able to understand each part of this diagram.
Recap: Finite Fields
One of the key tasks of cryptographic proof systems is to operate on large amounts of data while keeping the numbers small. If you can compress a statement about a large program into a mathematical equation with a few numbers, but those numbers are as large as the original program, you have gained nothing.
To do complex arithmetic while keeping numbers small, cryptographers often use modular arithmetic. We choose a prime number "modulus" p. The % operator means "take the remainder": 15%7=1, 53%10=3, and so on. (Note that the answer is always non-negative, so for example -1%10=9) You may have seen modulo in the context of adding and subtracting time (e.g., what time is 4 hours after 9? But here, we don’t just add and subtract modulo a number, we can also multiply, divide, and take exponents. We redefine: The above rules are all self-consistent. For example, if p=7, then: 5+3=1 (because 8%7=1) 1-3=5 (because -2%7=5) 2*5=3 3/5=2 A more general term for this kind of structure is a finite field. A finite field is a mathematical structure that follows the usual laws of arithmetic, but in which there are a finite number of possible values, so each value can be represented by a fixed size. Modular arithmetic (or prime field) is the most common type of finite field, but there is another type: an extension field. You may have seen one extension field: the complex numbers. We "imagine" a new element and label it i, and do math with it: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. We can do the same with the extension of the prime field. As we start dealing with smaller fields, the extension of prime fields becomes increasingly important for security, and binary fields (which Binius uses) Entirely dependent on extensions to have practical utility.
Recap: Arithmetization
The way SNARKs and STARKs prove computer programs is through arithmetic: you take a statement about the program you want to prove, and turn it into a mathematical equation involving a polynomial. Valid solutions to the equation correspond to valid executions of the program.
As a simple example, suppose I computed the 100th Fibonacci number, and I want to prove to you what it is. I create a polynomial F that encodes the Fibonacci sequence: so F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 and so on for 100 steps. The condition I need to prove is that F(x+2)=F(x)+F(x+1) over the entire range x={0,1…98}. I can convince you by giving you the quotient: where Z(x) = (x-0) * (x-1) * …(x-98). If I can provide that F and H satisfy this equation, then F must satisfy F(x+2)-F(x+1)-F(x) in the range. If I additionally verify that for F, F(0)=F(1)=1, then F(100) must actually be the 100th Fibonacci number.
If you want to prove something more complicated, then you replace the “simple” relation F(x+2) = F(x) + F(x+1) with a more complicated equation that basically says “F(x+1) is the output of initializing a virtual machine whose state is F(x)”, and run a computational step. You can also replace the number 100 with a larger number, for example, 100000000, to accommodate more steps.
All SNARKs and STARKs are based on the idea of using simple equations over polynomials (and sometimes vectors and matrices) to represent a large number of relationships between individual values. Not all algorithms check for equivalence between adjacent computational steps like the above: for example, PLONK does not, and neither does R1CS. But many of the most efficient checks do, because it is easier to minimize overhead by performing the same check (or the same few checks) many times.
Plonky2: From 256-bit SNARKs and STARKs to 64-bit...only STARKs
Five years ago, a reasonable summary of the different types of zero-knowledge proofs was as follows. There are two types of proofs: (elliptic curve-based) SNARKs and (hash-based) STARKs. Technically, STARKs are a type of SNARK, but in practice, it's common to use "SNARK" to refer to the elliptic curve-based variant and "STARK" to refer to the hash-based construction. SNARKs are small, so you can verify them very quickly and install them on-chain easily. STARKs are large, but they don't require a trusted setup, and they're quantum-resistant.

△ STARK works by treating the data as a polynomial, computing the computation of that polynomial, and using the Merkle root of the extended data as a "polynomial commitment".
A key piece of history here is that SNARKs based on elliptic curves were first widely used: STARKs didn't become efficient enough until around 2018, thanks to FRI, and by then Zcash had been running for over a year. Elliptic curve-based SNARKs have a key limitation: if you want to use an elliptic curve-based SNARK, then the arithmetic in these equations must be done using the point modulus on the elliptic curve. This is a large number, usually close to 2^256: for example, the bn128 curve has 21888242871839275222246405745257275088548364400416034343698204186575808495617. But real computations use small numbers: if you think about a "real" program in your favorite language, most of the things it uses are counters, indices in for loops, positions in the program, single bits representing True or False, and other things that are almost always only a few digits long.
Even if your "original" data consists of "small" numbers, the proof requires computing quotients, expansions, random linear combinations, and other transformations of the data that will result in an equal or larger number of objects that are on average as large as the full size of your field. This creates a key inefficiency: to prove a computation on n small values, you have to do more computation on n much larger values. Initially, STARKs inherited the SNARK habit of using 256-bit fields, and thus suffered from the same inefficiency.

△ Reed-Solomon expansion of some polynomial evaluations. Although the original values are small, the additional values will all expand to the full size of the field (in this case 2 to the power of 31 -1)
In 2022, Plonky2 was released. The main innovation of Plonky2 is to perform arithmetic modulo a small prime number: 2 to the power of 64 – 2 to the power of 32 + 1 = 18446744067414584321. Now, each addition or multiplication can always be done in a few instructions on the CPU, and hashing all the data together is 4 times faster than before. But there is a problem: this method only works for STARKs. If you try to use SNARKs, elliptic curves will become insecure for such a small elliptic curve.
To ensure security, Plonky2 also needs to introduce extension fields. A key technique for checking arithmetic equations is "random point sampling": if you want to check whether H(x) * Z(x) is equal to F(x+2)-F(x+1)-F(x), you can randomly choose a coordinate r, provide a polynomial commitment to open a proof proving H(r), Z(r), F(r), F(r+1) and F(r+2), and then verify whether H(r) * Z(r) is equal to F(r+2)-F(r+1)-F(r). If an attacker can guess the coordinates in advance, then the attacker can deceive the proof system - this is why the proof system must be random. But this also means that the coordinates have to be sampled from a set large enough that the attacker can't just guess at random. This is obviously true if the modulus is close to 2^256. But we're not there yet for modulos of 2^64 -2^32 +1, and it's certainly not the case if we get down to 2^31 -1. It's well within the capabilities of an attacker to try to forge a proof two billion times until one gets lucky.
To thwart this, we sample r from an extended field, so for example, you could define y where y^3 = 5, and take a combination of 1, y, and y^2. This brings the total number of coordinates to about 2^93. Most of the polynomials that the prover computes don't go into this extended field; they're just integers modulo 2^31 -1, so you still get all the efficiency you get from using a small field. But random point checking and FRI calculations do reach deep into this larger realm to get the security they need.
From Small Primes to Binary
Computers do arithmetic by representing larger numbers as sequences of 0s and 1s, and building "circuits" on top of those bits to compute operations like addition and multiplication. Computers are particularly optimized for 16-, 32-, and 64-bit integers. For example, 2^64 -2^32 +1 and 2^31 -1 were chosen not only because they fit within those bounds, but also because they fit well within them: multiplication modulo 2^64 -2^32 +1 can be performed by doing a regular 32-bit multiplication, and bitwise shifting and copying the output in a few places; this article explains some of the tricks nicely.
However, a better approach is to do the calculations directly in binary. What if addition could be “just” XOR, without having to worry about “carrying” overflow from adding 1+1 from one bit to the next? What if multiplication could be more parallelized in the same way? These advantages are all based on being able to represent true/false values with a single bit.
Getting these advantages of doing binary computation directly is exactly what Binius is trying to do. The Binius team demonstrated the efficiency gains in their zkSummit talk:
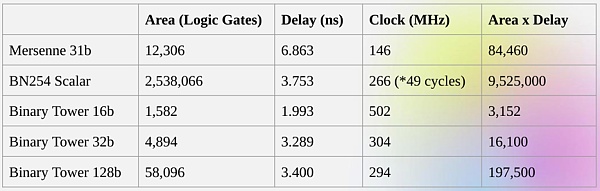
Despite being roughly the same “size”, 32-bit binary field operations require 5 times less computational resources than 31-bit Mersenne field operations.
From a Univariate Polynomial to a Hypercube
Suppose we believe this reasoning, and want to do everything with bits (0 and 1). How can we represent a billion bits with a single polynomial?
Here we face two practical problems:
For a polynomial to represent a large number of values, those values need to be accessible when evaluating the polynomial: F(0), F(1) … F(100) in the Fibonacci example above, and in a larger computation the exponents would run into the millions. The fields we use need to contain numbers up to this size.
Proving any value we commit in a Merkle tree (like all STARKs) requires Reed-Solomon encoding it: for example, extending the values from n to 8n, using redundancy to prevent malicious provers from cheating by forging a value during the computation. This also requires having a large enough field: to extend a million values to 8 million, you need 8 million different points to compute the polynomial.
A key idea of Binius is to solve these two problems separately, and do so by representing the same data in two different ways. First, the polynomial itself.
Systems like elliptic curve-based SNARKs, 2019-era STARKs, Plonky2, etc. usually deal with polynomials over one variable: F(x). Binius, on the other hand, takes inspiration from the Spartan protocol and uses multivariate polynomials: F(x1,x2,… xk). In effect, we represent the entire computational trajectory on a computational "hypercube" where each xi is either 0 or 1. For example, if we want to represent a Fibonacci sequence, and we still use a field large enough to represent them, we can imagine the first 16 of them like this:

That is, F(0,0,0,0) should be 1, F(1,0,0,0) is also 1, F(0,1,0,0) is 2, and so on, all the way up to F(1,1,1,1) = 987. Given such a computational hypercube, there is a multivariate linear (degree 1 in each variable) polynomial that produces these computations. So we can think of this set of values as a representation of the polynomial; we don't need to compute the coefficients.
This example is of course just for illustration: in practice, the whole point of going into the hypercube is to let us deal with single bits. The "Binius-native" way to compute Fibonacci numbers is to use a higher-dimensional cube, storing one number per group of, say, 16 bits. This requires some cleverness to implement integer addition on a bit-by-bit basis, but for Binius, it's not too hard.
Now, let's look at erasure codes. The way STARKs work is that you take n values, Reed-Solomon-extend them to a larger number of values (usually 8n, but often between 2n and 32n), then randomly select some Merkle branches from the extension and perform some kind of check on them. The hypercube is of length 2 in each dimension. Therefore, it's not practical to expand it directly: there's not enough "room" to sample Merkle branches from 16 values. So how do we do it? Let's assume the hypercube is a square!
Simple Binius - An Example
For a python implementation of the protocol, please copy the following link to your browser: https://github.com/ethereum/research/blob/master/binius/simple_binius.py
Let's look at an example, using regular integers as our fields for convenience (in the actual implementation, binary field elements will be used). First, we encode the hypercube we want to submit as a square:
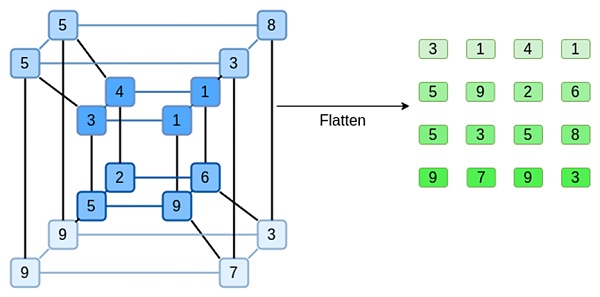
Now, we expand the square using Reed-Solomon. That is, we treat each row as a degree 3 polynomial evaluated at x = {0,1,2,3}, and evaluate the same polynomial at x = {4,5,6,7}:

Note that the numbers can get really big quickly! This is why in real implementations, we always use finite fields, rather than regular integers: if we used integers modulo 11, for example, the expansion of the first row would just be [3,10,0,6].
If you want to try out the expansion and verify the numbers yourself, you can use my simple Reed-Solomon expansion code here.
Next, we treat this expansion as columns, and create a Merkle tree of the columns. The root of the Merkle tree is our commitment.
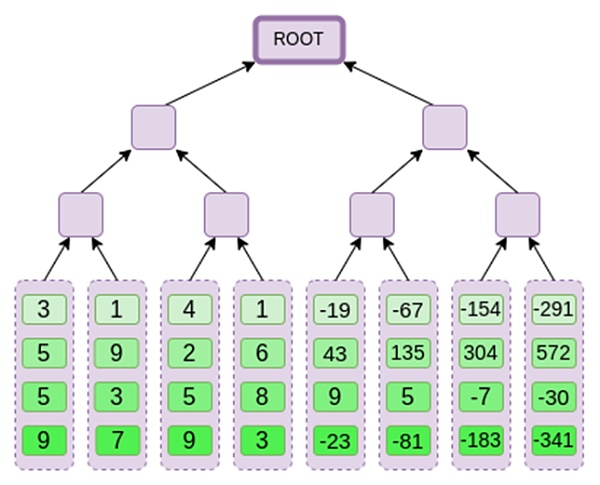
Now, let's assume that the prover wants to prove the computation of this polynomial r={r0,r1,r2,r3} at some point. There is a subtle difference in Binius that makes it weaker than other polynomial commitment schemes: the prover should not know or be able to guess s before committing to the Merkle root (in other words, r should be a pseudo-random value that depends on the Merkle root). This makes the scheme useless for "database lookups" (e.g., "OK, you gave me the Merkle root, now prove to me P(0,0,1,0)!").
But the zero-knowledge proof protocols we actually use usually don't require "database lookups"; they only need to check the polynomial at a random evaluation point. So this restriction serves our purposes.
Suppose we choose r={1,2,3,4} (the polynomial evaluates to -137 at this point; you can confirm this using this code ). Now, we get into the proof. We split r into two parts: the first part {1,2} represents the linear combination of the columns within the row, and the second part {3,4} represents the linear combination of the rows. We compute a "tensor product", for the columns:
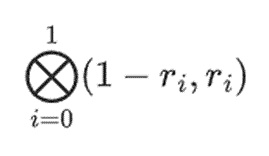
and for the rows:

This means: a list of all possible products of a value in each set. In the row case, we get: [(1-r2)*(1-r3), (1-r3), (1-r2)*r3, r2*r3] Using r={1,2,3,4} (so r2=3 and r3=4): [(1-3)*(1-4), 3*(1-4),(1-3)*4,3*4] = [6, -9 -8 -12] Now, we compute a new "row" t by taking linear combinations of the existing rows. That is, we take: You can think of what's happening here as a partial evaluation. If we multiply the full tensor product by the full vector of all values, you'll get the computation P(1,2,3,4) = -137. Here, we've multiplied the partial tensor products of only half of the evaluation coordinates and reduced the grid of N values to a row of square root N values. If you give this row to someone else, they can do the rest of the computation with the tensor products of the other half of the evaluation coordinates. The prover gives the following new row to the verifier: t along with a Merkle proof of some randomly sampled columns. In our illustrative example, we'll have the prover provide only the last column; in real life, the prover would need to provide dozens of columns to achieve adequate security.
Now, we exploit the linearity of Reed-Solomon codes. The key property we use is that taking a linear combination of Reed-Solomon expansions gives the same result as taking a Reed-Solomon expansion of a linear combination. This "sequential independence" generally occurs when both operations are linear.
The verifier does just that. They compute t, and compute linear combinations of the same columns that the prover computed before (but only the columns provided by the prover), and verify that the two procedures give the same answer.
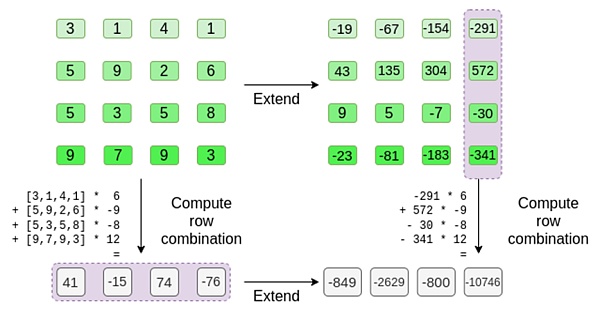
In this case, it’s expanding t, computing the same linear combination ([6,-9,-8,12], which both give the same answer: -10746. This proves that the Merkle root was constructed “in good faith” (or at least “close enough”), and that it matches t: at least the vast majority of the columns are compatible with each other.
But there’s one more thing the verifier needs to check: check the evaluation of the polynomial {r0…r3}. None of the steps the verifier has taken so far actually depended on the value the prover claimed. Here’s how we check it. We take the tensor product of the “column parts” that we marked as computation points:
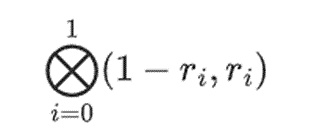
In our case, where r={1,2,3,4} so the half of the columns chosen is {1,2}), this is equal to:

Now we take this linear combination t:
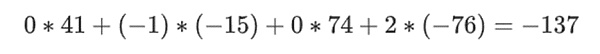
This is the same as taking the polynomial directly.
The above is very close to a complete description of the "simple" Binius protocol. This already has some interesting advantages: for example, since the data is split into rows and columns, you only need a field that is half the size. However, this does not achieve the full benefits of computing in binary. For that, we need the full Binius protocol. But first, let's take a closer look at binary fields. The smallest possible field is arithmetic modulo 2, which is so small that we can write addition and multiplication tables for it: We can get larger binary fields by extension: If we start with F2 (integers modulo 2) and then define x where x squared = x + 1, we get the following addition and multiplication tables: It turns out that we can extend binary fields to arbitrarily large sizes by repeating this construction. Unlike complex numbers over real numbers, where you can add a new element but never add any more elements I (quaternions do exist, but they are mathematically weird, e.g. ab is not equal to ba), with finite fields you can add new extensions forever. Specifically, we define elements as follows:
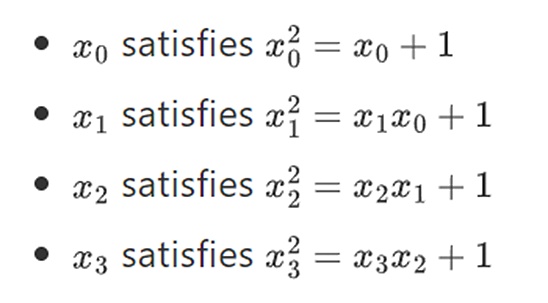
and so on…. This is often called a tower construction, because each successive extension can be thought of as adding a new layer to the tower. This is not the only way to construct binary fields of arbitrary size, but it has some unique advantages that Binius exploits.
We can represent these numbers as lists of bits. For example, 1100101010001111. The first bit represents multiples of 1, the second bit represents multiples of x0, and then subsequent bits represent multiples of the following x1 numbers: x1, x1*x0, x2, x2*x0, and so on. This encoding is nice because you can break it down:
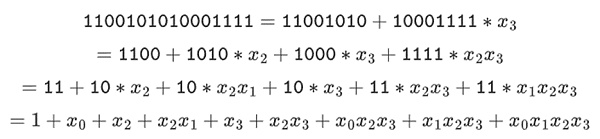
This is a relatively uncommon representation, but I like to represent binary field elements as integers with the more efficient bit on the right. That is, 1=1, x0=01=2, 1+x0=11=3, 1+x0+x2=11001000 =19, and so on. In this expression, that's 61779.
Addition in the binary field is just XOR (and so is subtraction, by the way); note that this means x+x=0 for any x. To multiply two elements x*y together, there's a very simple recursive algorithm: split each number in half:
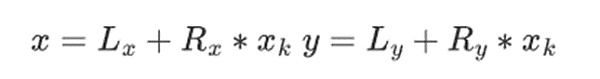
Then, split the multiplication:
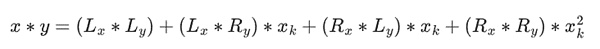
The last part is the only one that's a little tricky, because you have to apply the simplification rule. There are more efficient ways to do the multiplication, similar to Karatsuba's algorithm and Fast Fourier Transforms, but I'll leave that as an exercise for the interested reader to figure out.
Division in binary fields is done by combining multiplication and inversion. The "simple but slow" inversion method is an application of the generalized Fermat's little theorem. There is also a more complex but more efficient inversion algorithm, which you can find here. You can use the code here to play with addition, multiplication, and division of binary fields.
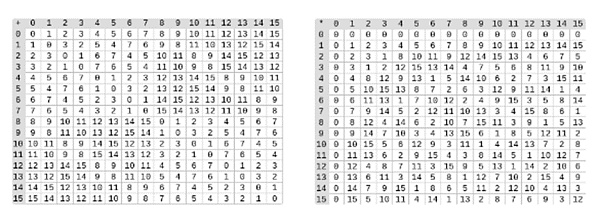
△ Left: Addition table for four-bit binary field elements (i.e., consisting of only 1, x0, x1, x0x1). Right: Multiplication table for four-bit binary field elements.
The beauty of this type of binary field is that it combines some of the best parts of "regular" integers and modular arithmetic. Like regular integers, binary field elements are unbounded: you can extend them at will. But just like modular arithmetic, if you operate on values within a certain size limit, all your results will stay in the same range. For example, if you take 42 to successive powers, you get:

After 255 steps, you're back to 42 to the 255th power = 1, and just like positive integers and modular arithmetic, they obey the usual laws of math: a*b=b*a, a*(b+c)=a*b+a*c, and even some weird new laws.
Finally, binary fields make it convenient to work with bits: if you do math with numbers that fit in 2 to the kth power, then all your output will fit in 2 to the kth power of bits, too. This avoids awkwardness. In Ethereum’s EIP-4844, the individual “chunks” of a blob must be numbers modulo 52435875175126190479447740508185965837690552500527637822603658699938581184513, so encoding binary data requires throwing away some space and doing extra checks at the application layer to ensure that the value stored for each element is less than 2^248.
This also means that binary field operations are super fast on computers — both CPUs and theoretically optimal FPGA and ASIC designs.
This all means that we can do Reed-Solomon encoding like we did above, in a way that completely avoids integer “explosion” as we saw in our example, and in a very “native” way, the kind of calculations that computers are good at. The “split” property of binary fields — how we made 1100101010001111 = 11001010 + 10001111 * x3, and then split it however we wanted — is also crucial to achieve a lot of flexibility.
Full Binius
For a python implementation of the protocol, copy the following link to your browser: https://github.com/ethereum/research/blob/master/binius/packed_binius.py
Now, we can move on to “Full Binius,” which adapts “Simple Binius” to (i) work on binary fields and (ii) let us commit individual bits. This protocol is difficult to understand because it switches back and forth between different ways of looking at the bit matrix; it certainly took me longer to understand it than it usually takes me to understand cryptographic protocols. But once you understand binary fields, the good news is that the "harder math" that Binius relies on doesn't exist.
This isn't elliptic curve pairings, where there are deeper and deeper algebraic geometry rabbit holes to go down; here, you just need binary fields.
Let's look at the full diagram again:

By now, most of the components should be familiar to you. The idea of "flattening" a hypercube into a grid, the idea of computing row and column combinations as tensor products of evaluation points, and the idea of checking the equivalence between "Reed-Solomon expansion then computing row combinations" and "computing row combinations then Reed-Solomon expansion" are all implemented in simple Binius.
What's new in "full Binius"? There are basically three things going on:
The individual values in the hypercube and square must be bits (0 or 1).
The expansion process expands bits into more bits by grouping them into columns and temporarily assuming that they are elements of a larger field.
After the row grouping step, there is an element-wise "decomposition into bits" step that converts the expansion back into bits.
We'll discuss both of these in turn. First, the new extension procedure. Reed-Solomon codes have a fundamental limitation that if you want to expand n to k*n, you need to work in a field with k*n distinct values that can be used as coordinates. With F2 (aka bits), you can't do that. So what we do is "pack" adjacent F2 elements together to form larger values. In the example here, we pack two bits at a time into the {0, 1, 2, 3} elements, which is enough for us since our extension only has four computation points. In a "real" proof, we might go back 16 bits at a time. We then perform the Reed-Solomon code on these packed values and unpack them back into bits again.

Now, the row combinations. In order to make the "evaluate at a random point" check cryptographically secure, we need to sample that point from a fairly large space (much larger than the hypercube itself). So while the points inside the hypercube are bits, the computation values outside the hypercube will be much larger. In the example above, the "row combination" ends up being [11,4,6,1].
This presents a problem: we know how to group bits into a larger value and then perform a Reed-Solomon expansion on that, but how do we do the same thing for larger pairs of values?
Binius's trick is to do it bit by bit: we look at a single bit of each value (e.g., for the thing we labeled "11," that's [1,1,0,1]), and then expand it row by row. We perform the expansion on the object. That is, we perform the expansion process on 1 row of each element, then on the x0 row, then on the "x1" row, then on the x0x1 row, and so on (ok, in our toy example we stop there, but in a real implementation we'll go up to 128 rows (the last one being x6*...*x0))
To recap
We took the bits in the hypercube and converted them into a grid. Then, we treated groups of adjacent bits on each row as elements of a larger field and performed arithmetic operations on them to Reed-Solomon expand the row.
Next, we take the row combinations of the bits in each column and get the columns of bits for each row as the output (much smaller for squares larger than 4x4).
Finally, we treat the output as a matrix and its bits as rows.
Why is this the case? In "normal" math, if you start slicing a number bit by bit, the ability to (usually) do linear operations in any order and get the same result breaks down.
For example, if I start with the number 345, and I multiply it by 8, and then by 3, I get 8280, and if I reverse those two operations, I also get 8280. But if I insert a "bitwise split" operation between the two steps, it breaks down: If you do 8x and then 3x, you get:
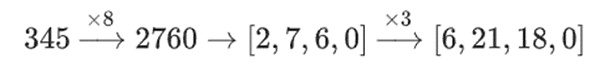
However, if you do 3x and then 8x, you get:
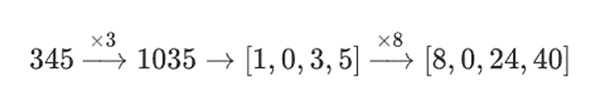
But in binary fields built with tower structures, this approach does work. The reason is their separability: if you multiply a large value by a small value, what happens on each segment, stays on each segment. If we multiply 1100101010001111 by 11, this is the same as first factoring 1100101010001111 as

then multiplying each component by 11 separately.
Putting it all together
In general, zero-knowledge proof systems work by making statements about polynomials while also making statements about the underlying evaluation: just like we saw in the Fibonacci example, F(X+2)-F(X+1)-F(X) = Z(X)*H(X) while checking all the steps of the Fibonacci calculation. We check statements about polynomials by proving the evaluation at random points. This check of a random point represents a check of the entire polynomial: if the polynomial equation doesn't match, there's a small chance that it will match at a particular random coordinate.
In practice, one of the main reasons for this inefficiency is that in real programs, most of the numbers we deal with are small: indices in for loops, True/False values, counters, and things like that. However, when we "extend" data with Reed-Solomon encoding to give us the redundancy needed to make Merkle-proof-based checks safe, most of the "extra" values end up taking up the entire size of the field, even if the original value was small.
To fix this, we want to make this field as small as possible. Plonky2 took us from 256-bit numbers to 64-bit numbers, and then Plonky3 went further to 31 bits. But even that is not optimal. With binary fields, we can deal with single bits. This makes the encoding "dense": if your actual underlying data has n bits, then your encoding will have n bits, and the expansion will have 8*n bits, with no extra overhead.
Now, let's look at this diagram for the third time:

In Binius, we work on a multilinear polynomial: a hypercube P(x0,x1,…xk) where a single evaluation of P(0,0,0,0), P(0,0,0,1) up to P(1,1,1,1), holds the data we care about. To prove a computation at a certain point, we "reinterpret" the same data as a square. We then extend each row, using Reed-Solomon encoding to provide the data redundancy needed for safety with randomized Merkle branch queries. We then compute random linear combinations of the rows, designing the coefficients so that the new combined rows actually contain the computed values we care about. Both this newly created row (reinterpreted as a row of 128 bits) and some randomly chosen columns with Merkle branches are passed to the verifier.
The verifier then performs the "expanded row combination" (or more precisely, the expanded columns) and the "expanded row combination" and verifies that the two match. A column combination is then computed and checked to see if it returns the value asserted by the prover. This is our proof system (or more precisely, the polynomial commitment scheme, which is a key component of the proof system).
What haven't we covered yet?
Efficient algorithms to expand rows, which are required to actually make the verifier computationally efficient. We use the Fast Fourier Transform on binary fields, described here (although the exact implementation will be different, as this post uses a less efficient construction that is not based on recursive expansion).
Arithmeticization. Univariate polynomials are convenient because you can do things like F(X+2)-F(X+1)-F(X) = Z(X)*H(X) to link adjacent steps in the computation. In the hypercube, “next step” is much less well explained than “X+1”. You can do X+k, powers of k, but this jumping behavior sacrifices many of Binius’ key advantages. The Binius paper describes a solution. See Section 4.3), but this is a “deep rabbit hole” in itself.
How to safely do specific value checks. The Fibonacci example requires checking key boundary conditions: the value of F(0)=F(1)=1 and F(100). But with “original” Binius, it’s unsafe to do this check at a known computation point. There are some fairly simple ways to convert known computation checks into unknown computation checks, using so-called sum-checking protocols; but we won't cover those here.
Lookup protocols, another technique that has recently become widely used to make super-efficient proof systems, are used to make super-efficient proof systems. Binius can be used in conjunction with lookup protocols for many applications.
Beyond square root verification times. Square roots are expensive: a Binius proof of 2^32 bits is about 11MB long. You can compensate for this by using other proof systems to make "proofs of Binius proofs", which give you the efficiency of a Binius proof and the smaller proof size. Another option is the more complex FRI-binius protocol, which creates a proof of multi-logarithmic size (just like regular FRI).
How Binius impacts "SNARK-friendliness". The basic summary is that if you use Binius, you no longer need to care about making computations "arithmetic-friendly": regular hashing is no longer more efficient than traditional arithmetic hashing, multiplication modulo 2 to the power of 32 or modulo 2 to the power of 256 is no longer as much of a headache as multiplication modulo 2, and so on. But this is a complex topic. A lot of things change when everything is done in binary.
I expect to see more improvements in binary field-based proof techniques in the coming months.
"Ethereum alignment" includes value alignment, technical alignment, and economic alignment.
 JinseFinance
JinseFinanceThe premise for understanding this article is that you already know the basic principles of SNARKs and STARKs. If you are not familiar with them, it is recommended that you read the first few parts of this article to understand the basics.
 JinseFinance
JinseFinanceETH, interpretation of Vitalik’s latest article Golden Finance, the soul of Ethereum and the essence of the crypto world remain.
 JinseFinance
JinseFinanceVitalik has joined forces with four co-authors to unveil in a research paper that introduces a technological marvel known as "privacy pools," designed to address one of the most pressing issues in the blockchain sphere.
 Catherine
CatherineThe new update includes “The Scourge” which would help to solve MEV issues.
 Beincrypto
BeincryptoWhat a decade of essays – covering everything from Soulbound tokens to superrational DAOs – says about Ethereum and crypto.
 Coindesk
CoindeskThe inventor of Ethereum Vitalik Buterin and his father Dmitry “Dima” Buterin talked about the crypto market, volatility, and speculators. ...
 Bitcoinist
BitcoinistCompared with PoW, PoS is a better blockchain security mechanism.
 链向资讯
链向资讯Compared with PoW, PoS is a better blockchain security mechanism.
 Ftftx
FtftxThe small southeast European nation is beginning to sift through the murky waters of blockchain regulation by granting the Ethereum co-founder citizenship.
 Cointelegraph
Cointelegraph