FHE: Protecting Data Privacy

Source: IOBC Capital

In the digital age, the protection of data privacy is more important than ever. With the rapid development of big data, cloud computing and the Internet of Things, the collection, storage and analysis of personal information have become increasingly common. However, this also brings the risk of data leakage and abuse.

FHE stands for Fully Homomorphic Encryption, which allows calculations to be performed directly on encrypted data, and the calculation results obtained are consistent with the results of the same calculations on the original data. This means that we can process and analyze data without exposing the original data, which provides a new solution for protecting data privacy and integrity.

The theoretical basis of FHE can be traced back to 1978, when Rivest et al. proposed the first homomorphic encryption problem. It was not until 2009 that Gentry first constructed a feasible fully homomorphic encryption scheme in his doctoral thesis, and FHE research really began to flourish. The early FHE schemes had extremely low computational efficiency and could not meet the needs of practical applications. As researchers continue to propose optimization schemes, the performance of FHE has been significantly improved. FHE research is moving towards improving efficiency, reducing computational complexity and expanding application scenarios.

Technical Implementation Path of FHE

FHE Scheme Based on Ideal Lattice

This is currently recognized as the most practical and efficient FHE construction method. The main idea is to use the algebraic structure of ring operations to complete encryption and decryption operations through modular operations and decomposition of the ideal factors of the ring. Representative schemes include BGV, BFV and CKKS. The advantages of such schemes are high computational efficiency, and the disadvantages are that they require larger key and ciphertext space.

Matrix-based FHE Scheme

This scheme encodes plaintext information into a matrix and achieves homomorphism through matrix operations. Representative schemes include GSW and HiNC, which are characterized by high security but low efficiency.

NTRU-based FHE scheme

NTRU (Number Theory Research Unit) has a good algebraic structure and cyclic symmetry, and can be used to construct efficient FHE schemes, such as YASHE and NTRU-FHE. The advantages of these schemes are that the key and ciphertext sizes are small and suitable for resource-constrained environments.

FHE schemes based on learning arithmetic circuits with noise (LWE/LWR)

Encryption schemes constructed based on LWE/LWR problems, such as FHEW and TFHE, focus more on theoretical innovation and can achieve very strong security, but their practicality is limited.

FHE vs. ZKP

FHE and ZKP are both encryption technologies, but they are almost complementary.

ZKP allows the prover to prove to the verifier that a piece of information is correct without revealing specific details. The verifier can verify the correctness of the information and the integrity of the calculation without re-performing the calculation. Although ZKP can prove correctness without leaking information, its input is usually in plain text, which may lead to privacy leakage.

The introduction of FHE can solve this problem. FHE can perform arbitrary calculations on encrypted data without decryption, thereby protecting data privacy. However, the problem with FHE is that it cannot ensure the correctness and reliability of the calculation, which is exactly the problem solved by ZKP.

Through the technical combination of FHE+ZKP, on the one hand, FHE protects the privacy of input data and calculation process, and on the other hand, ZKP provides cryptographic proof of correctness, legality and auditability for FHE calculation, ultimately realizing truly secure and reliable privacy computing, which is very valuable for privacy protection application scenarios such as sensitive data processing and multi-party cooperative computing.

ZAMA: FHE Pioneer

Zama is an open source cryptography company that builds state-of-the-art FHE solutions for blockchain and AI. There are four main open source solutions:

TFHE-rs is a Rust implementation of fully homomorphic encryption on Torus for performing Boolean and integer operations on encrypted data. The TFHE-rs library implements the Zama variant of TFHE, which implements all required homomorphic operations such as addition and function evaluation through programmable bootstrapping.

Concrete is an open source FHE framework that includes a TFHE compiler as part of the framework, which converts regular programming code into actionable instructions that computers can execute using FHE, making it easy for developers to write FHE programs. Computing on FHE encrypted data can introduce a lot of noise, which can lead to errors. Concrete has a very low default error probability, and developers can flexibly modify the parameters of this error probability.

Concrete ML is an open source privacy-preserving machine learning (PPML) tool built on Concrete. Developers can integrate FHE into machine learning models without cryptography knowledge.

fhEVM introduces FHE to the EVM ecosystem, allowing developers to execute encrypted smart contracts on the chain, and protect the privacy of on-chain data while making smart contracts composable. While integrating TFHE-rs, fhEVM introduces a new TFHE Solidity library, allowing developers to use Solidity to calculate encrypted data.

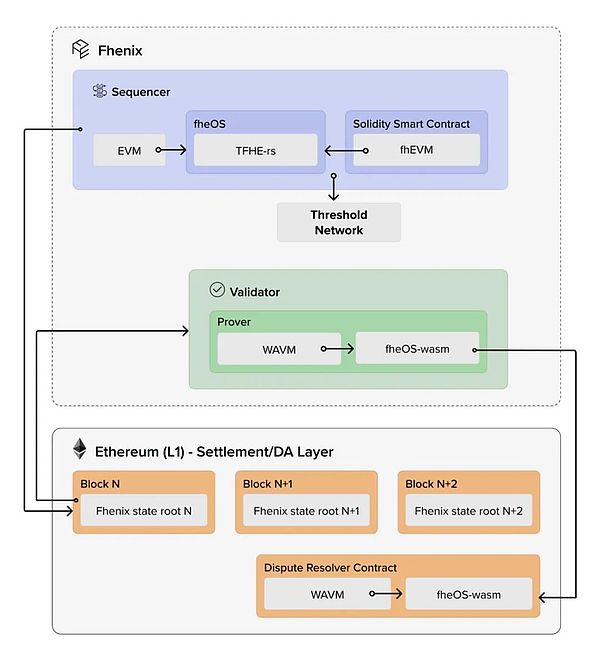
Fhenix: The First FHE-Rollup

Fhenix is ​​the first Layer2 Rollup based on FHE. It builds its own cryptographic computing library, fheOS, based on Zama's TFHE-rs. It contains precompiled common cryptographic opcodes, enabling smart contracts to use FHE primitives on the chain. fheOS is also responsible for the communication and authentication between the rollup and the Threshold Service Network (TSN) for decryption and re-encryption requests, while proving that the decryption request is legitimate. The fheOS library is designed to be injected into any existing EVM version as an extension and is fully compatible with the EVM.

Fhenix's consensus mechanism uses Arbitrum's Nitro prover. The reason for choosing the fraud proof method is that the underlying structure of FHE and zkSNARK is different. The use of ZKP to verify FHE is very computationally intensive and almost impossible at the current technical stage.

Fhenix has also recently cooperated with EigenLayer to develop FHE coprocessors, introducing FHE calculations to other public chains, L2, L3, etc. Since Fhenix uses fraud proofs and there is a 7-day challenge period, EigenLayer's services can help the coprocessor achieve fast transaction confirmation and significantly improve performance.

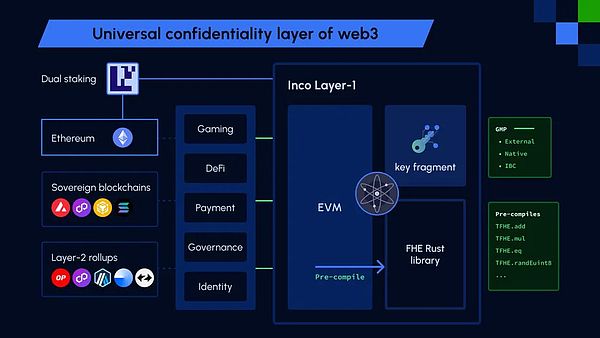
Inco Network: Confidentiality as a Service

Inco is a modular trusted computing Layer1 that can be used as a universal privacy layer for Web3. It supports fhEVM, enabling developers to quickly build privacy Dapps using the Solidity language and development tools in the Ethereum ecosystem. At the same time, Inco provides CaaS services to EVM and Cosmos chains that lack native encryption through bridging and IBC protocols. The CaaS service mainly includes three functions:

On-chain encrypted state: store encrypted data directly on the chain without off-chain storage;

Composable encrypted state: perform state transitions on encrypted data completely on the chain without decryption;

On-chain randomness: generate random numbers for applications on the chain, without the need for external randomness services, and be able to build applications directly on the chain.

Currently, Inco has some use cases such as games, NFTs, RWA, voting governance, DID, etc.

Mind Network: FHE Restaking Layer

Mind is the first FHE Restaking layer tailored for AI and POS networks. As the Restaking layer, it accepts restaking tokens from ETH, BTC and AI blue chip companies for staking; at the same time, as an FHE verification network, it uses FHE technology to verify the data of each node to reach a consensus and ensure data integrity and security. Mind provides economic security for decentralized AI, Depin, EigenLayer AVS, Babylon AVS and key POS networks, maintaining the consensus and credibility of the entire system.

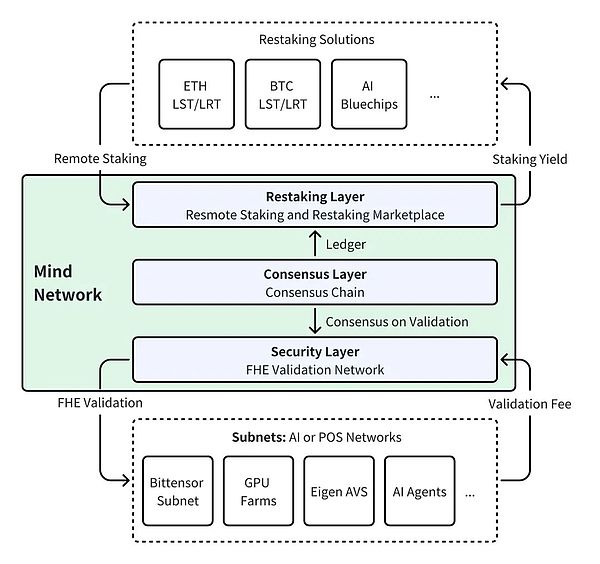
Restaking layer: Cooperate with EigenLayer, StakeStone, Renzo, Babylon, Ankr, etc. to obtain security from Ethereum and Bitcoin networks; cooperate with Chainlink CCIP, Connext, etc. to achieve cross-chain remote restaking.

Security layer:Introducing FHE enhanced verifiers to ensure end-to-end encryption of the verification and consensus calculation process, and further enhancing security by integrating Fhenix and Inco's fhEVM module.

Consensus layer:Introducing a Proof of Intelligence (POI) consensus mechanism designed specifically for AI tasks to ensure fair and secure reward distribution among FHE verifiers. In addition, Mind Network is working with AltLayer, EigenDA, and Arbitrum Orbit to launch a Rollup chain to enhance consensus calculations at lower costs and faster performance.

Privasea: Proof of Human

Privasea is a Depin+AI network for FHE machine learning. The technical architecture includes the following core components:

HESea library: This is an advanced FHE library that provides the ability to perform secure calculations on encrypted data. The library supports multiple FHE schemes, such as TFHE, CKKS, BGV/BFV, etc.

Privasea API: This is the application program interface of the Privasea AI network, which provides a series of functions and endpoints to simplify data submission, model training and prediction operations, and ensure the encryption of data during transmission and processing.

Privanetix: This is a decentralized computing network composed of multiple high-performance computing nodes that can efficiently process encrypted data. Each node is integrated with the HESea library to ensure data privacy and computing performance.

Privasea Smart Contract Suite: Based on the incentive mechanism of blockchain technology, the registration and contribution of Privanetix nodes are tracked through smart contracts, calculations are verified and rewards are distributed to ensure the enthusiasm and fairness of participants.

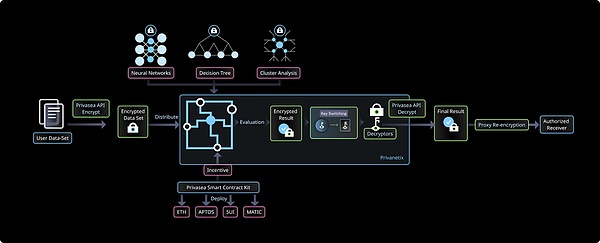
Privasea launched the ImHuman application and developed Proof of Human based on FHE, which aims to prove that users are human to protect their digital identities from the threat of robots and artificial intelligence impersonation. Users can verify that they are real humans through facial biometrics and generate a unique NFT as proof of their personal human identity. Using the ImHuman application, users can securely confirm their personal identity on Web3 and Web2 platforms without revealing personal details.

Written at the end

In the field of Defi, FHE enables transactions and capital flows without leaking sensitive financial information, thereby protecting user privacy and reducing market risks. It may also become one of the effective ways to solve the MEV problem; in full-chain games, FHE ensures that data such as players' scores and game progress are protected in an encrypted state, while allowing game logic to run on the chain without exposing data, enhancing the fairness and security of the game; in the field of AI, FHE allows encrypted data to be analyzed and model trained, which not only protects data privacy, but also promotes cross-institutional data sharing and cooperation, and promotes the development of safer and more compliant artificial intelligence applications.

FHE still faces many challenges in practicality and efficiency, but its unique theoretical foundation brings hope for overcoming bottlenecks. In the future, FHE is expected to significantly improve performance and expand application scenarios through algorithm optimization, hardware acceleration and other means, providing a more solid foundation for data privacy protection and secure computing.