ログイン/ 登録

現代の「知識ゼロの証明」を形成する10の必読エッセイ

JinseFinance

2024/11/13 19:39

従う

出典：Denchainコミュニティ

ゼロ知識証明は、過去40年間で劇的に進化し、これまでにない洗練された効率的なレベルに到達しました。今日、毎日新しい論文やプロジェクトが登場し、豊かなアイデアとイノベーションの基盤が築かれています。

どのように始まったのか気になりませんか？この記事では、ゼロ知識証明の歴史に飛び込み、この分野の形成に貢献した10の画期的な論文を探ります。

1-起源

ゴールドワッサー、ミカリ、ラッコフ - 知識の複雑さKnowledge Complexity in Interactive Proof Systems (1985) [^1]

最初のマイルストーンは、1985年の代表的な論文にさかのぼります！この論文は、今日でもゼロ知識証明の中核をなす、多くの用語と基礎概念を紹介しました。

まず、この論文では証明システムを定義しており、証明者と検証者という2つの確率的チューリング機械を含む2者間プロトコルとしてモデル化されている。証明システムの目的は、与えられた入力xが形式言語Lに属することを、証明者が検証者に納得させることである。相互作用の最後に、検証者は "accept "か "reject "を出力する。

2 - 最初のアプリケーション

Fiat, Shamir - 自分を証明する方法：識別と署名の問題に対する実践的解決法 (1986) [^2)

フィアットとシャミアによるこの論文は、ゼロ知識証明に関する基礎的な研究の1年後に発表され、これらの概念の最初の実用的な応用を紹介している。双方向の識別スキームと、非対話的な署名スキームである。この2つの主な違いは、識別スキームでは、第三者が有効な記録を作成することで、虚偽の陳述を確信させることができるという点である。一方、署名プロトコルでは、不誠実な証明者であっても、虚偽の陳述について自分自身を納得させることができないため、署名は偽造不可能となります。

識別スキームは、検証者がランダムなチャレンジを送信し、証明者がそれに応じて応答する対話型プロトコルとして、二次残差証明システムを適用する。署名スキームは、検証者のチャレンジをハッシュ関数への呼び出しに置き換えることでこれを変更する。

著者の名前に聞き覚えはありませんか？これは、現在Fiat-Shamirヒューリスティックとして広く知られている強力な一般的技術の最初の例です。これは、検証者のチャレンジをランダムな述語機械（実際には暗号ハッシュ関数）へのクエリに置き換えることで、あらゆるパブリックコインの対話型証明システムを非対話型証明システムに変換することを可能にする。

3-実際に何を証明できるのか？

ゴールドライヒ(Goldreich)、ミカリ(Micali)、ウィグダーソン(Wigderson) - 知識ゼロですべてのNP文を証明する方法と暗号プロトコル設計のための方法論 (1987) [^3]

この本は、暗号プロトコル設計のための方法論です。align: left;">この1986年の論文は、NPのあらゆる言語がゼロ知識証明システムを認識するという驚くべき結果を与えている。これは、追加的な情報を明らかにすることなく、多項式時間で検証可能なあらゆる文の真理を証明できることを意味するので重要である。著者らは、3-colourability of graphsの証明体系を提供することで、これを実証している。さらに、この証明は確率的暗号の存在のみを仮定している。

証明の直観は以下の通りである：各ラウンドにおいて、

証明者は3色のランダムな並べ替えを選ぶ。
プロヴァーはクエリされたノードの色を明らかにしてコミットメントを開く。
色が一致した場合、証明者は即座に拒否する。

このプロトコルを多項式回数実行することで、検証者は、各ステップで開口部の色が無作為化されるため、情報を学習することなく、証明者が有効な3色を知っていることを高い確率で確信できる！

この研究には、同様に注目に値する他の2つの論文がある：証明可能な内容はすべてゼロ知識で証明できる [^4]。PSPACE [^5]、これはIPがPSPACEと同じくらい強力であることを示している。

4 - PCPs and the origins of concise non-interactive proofs

Micali - 計算上信頼できる証明.strong>Computationally Reliable Proofs (2000) [^6]

2000年にMicaliが執筆したこの論文は、ゼロ知識証明の歴史に重要な貢献をしている。SNARKという用語がまだ作られていなかったにもかかわらず、最初のSNARK構成とみなすことさえできます！

ミカリの構成は、あらゆる確率検査可能証明(PCP)を、簡潔で非対話的な証明に変換する。 PCPは、少数のビットを読むだけで検証できる証明であり、重要な結果であるPCP定理 [^strong>は、少数のビットの証明である。 [^7]は、NPのすべての言語が、証明の定数ビットだけを読むことで検証できるPCPを持つことを示している！

ミカリの構成は、以下のようにメルクル木を使用している：

証明者は証明のためにメルクル木を構築し、検証者にその根を送ります。section>
検証者はチェックしたい特定のビットを問い合わせる。style="text-align: left;">証明者はそれらのビットの認証パスを提供し、検証者はそれらのパスを検証する。

この構築は、単にFiat-Shamirヒューリスティックを適用することで非対話的にすることができる（この変換の対話的バージョンはKilian [^8]によって提案された）。この論文では、計算効率にも焦点を当てている。実際には、検証者は証明全体を受け取る必要はなく、一定数のビットと認証パスだけを受け取ればよいので、証明は簡潔になる。このシステムの主な欠点は、PCPの構成が非実用的であることであり、そのため、実用的な論証を生成するPCPの一般化である対話型述語機械証明（IOPs）が開発された。

5 - 二重に効率的なIP

Goldwasser, Kalai.Rothblum - Delegated computation: Interactive proofs for Muggles (2015) [^9]

この論文は効率に強く焦点を当て、広く知られたGKRプロトコルを紹介している。プロトコルを紹介する。注目すべきは、検証者と証明者の両方が多項式時間で実行されることであり、インタラクティブな証明のために二重の効率を実現している。

プロトコルは、入力ファンインが2の算術回路について、証明者と検証者が合意するところから始まる。その後、証明者は入力値が与えられた回路の出力を送信する。プロトコルは回路をレイヤーごとに調べ、出力レイヤーから入力レイヤーへと進む。各ステップは、証明者が入力層に到達するまで、現在の層の宣言を前の層の宣言に減らし、そこで元の入力と一致するかどうかをチェックすることができる。

各ステップで使用される主なプリミティブはsum-checking protocol [^10]であり、これはブール超立方体上で定義される、オラクルアクセスを持つv変数多項式gの値の和について、証明者が検証者を納得させることができる対話的証明である。超立方体:

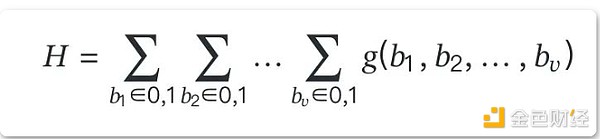
効率的で単純なため、和チェックプロトコルとGKRプロトコルは実際に広く使用されています。さらに詳しい説明は、Thalerのノート[^11]にこれらのプロトコルの別の概要がある。

6 - 最初の実用的なSNARK

Gennaro, Gentry.Parno, Raykova - Quadratic Span Programs and Succinct NIZKs without PCPs (2013) [^12]

ここで、実用的な最初のSNARKを記述した論文にジャンプします。論文にジャンプします！この研究は、非効率的なPCP定理に依存しないSNARKを作成することを目的としたSNARK研究の頂点に立つものです。PCP定理は理論的なSNARK構造を提供するが、実用的な応用には遅すぎるため、研究者はより効率的な代替案を見つけようとしてきた。例えば、Grothは2010年に双線形群とペアリングに基づく非対話的な論証システムを提案した[^13]。しかし、本論文は線形な証明者時間を実装しており、実用的なアプリケーションのための重要な改善である。

この研究は、Pinocchioプロトコル [^14]や、究極的に有名なGroth16 [^15]のような他の重要なプロトコルへの道を開いた。.また、これらのシステムにおいて重要な構成要素である二次スパン手続きと二次算術手続きについても記述している。

これらの構成要素の重大な欠点は、もっともらしいセットアップが必要なことであり、これは、公開参照文字列の生成段階で生成される秘密情報（しばしば有毒廃棄物と呼ばれる）が、正しく破棄されなければ、偽の証明を作成するために使用できることを意味する。偽の証明を作成することができる。さらに、このセットアップは汎用的ではないため、回路ごとに新しいセットアップが必要となる。このような制限があるにもかかわらず、生成される証明のサイズはさまざまな構成の中で最も小さいため、さまざまな用途によく使われます。

zk-SNARKを活用した初期の有力なブロックチェーンアプリケーションであるZerocash [^16]の最初の反復が、これらのシステムの上に構築されたことも注目に値します。

7 - PlonK SNARK

ガビゾン、ウィリアムソン。PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge (2019) [^17]

この2019年のインパクト論文では、多項式の対話的託宣証明(IOPs)に基づくシステムであるPlonK SNARKについて説明する。このシステムは、様々な多項式を使用する。このシステムは、多項式に関するステートメントを証明するために様々な多項式ガジェットを使用する。その中でも最も注目すべきものはGreat Product Argumentで、あるドメイン上の評価の積が1であることを証明することができる。これらのガジェットを使うことで、証明者は任意の算術回路の証明を構築することができ、検証者はそれを非対話的な方法で検証することができる。

実際には、オラクル・アクセスは多項式コミットメント・スキーム(PCS)によって実装され、これによって証明者は次のことができる:

commit to a polynomial and
provide evaluate that polynomial at a specific point その多項式を特定の点で評価する。strong>その多項式の開いた値を提供する。

これにより、検証者は任意の点で多項式を照会し、IOP関係を検証することができます。この論文で提案されているPCSはKZGコミットメントスキーム [^18]であり、効率的かつ実用的である。KZGは、証明者が多項式を1つの群要素としてコミットすることを可能にし、検証者はいくつかの楕円曲線ペアリングを計算することでオープン値を確認することができる。KZGはもっともらしいセットアップを必要とするが、セットアップ後はどのような回路でも使用できる汎用的なものである。しかし、PlonKは他のPCSスキームと組み合わせることで、透明な論証システムに適応させることができる。

さらに、PlonKの置換引数は、検索引数に触発された。lookup引数によって、証明者はシーケンスのすべての要素が別のシーケンスに含まれていることを示すことができます。ルックアップ引数により、証人をより小さなトレースに分解し、それらの間のルックアップ関係を証明することができるため、複雑な証明をより効率的に行うことができる。

8 - STARKs

Ben-Sasson, Bentov.Horesh, Riabzev - スケーラブルで透過的でポスト量子的な安全な計算の完全性 (2018) [^19]

Ben-Sasson, Bentov.: left;">本論文では、リードソロモン符号の近接テストのためのIOPプロトコルであるFRI[^20]に基づく、もう一つの一般的な証明システムであるSTARK証明システムについて説明する。STARKでは、証明者はあるドメイン上でメルクル木を構築することにより、多項式の評価をコミットする。コミットされた値は最初は未知であるため、証明者はFRIを使用して、これらの評価が十分に低次の有効な多項式を形成することを確認する。このプロトコルは多項式コミットメントスキームとしても使用でき、検証者は任意の時点でコミットメント多項式の評価を確認することができる。

STARKの最も説得力のある特徴の1つは、離散対数問題のような他の暗号学的仮定ではなく、暗号学的な耐衝突ハッシュ関数のみに依存していることです。耐衝突ハッシュ関数は量子攻撃下でも安全であると広く考えられているため、これはSTARKに潜在的なポスト量子セキュリティの点で優位性を与えます。加えて、STARKは透過的、つまり信頼されたセットアップを必要としません。また、汎用的であり、特定の回路に限定されないため、さまざまなアプリケーションに柔軟性を提供します。

9 - 再帰的

Valiant - です。漸進的に検証可能な計算や知識の証明は、時間的/空間的な効率を意味する (2008) [^21]

。長年に渡って浮上してきた重要な概念は再帰であり、これは単に、ある証明が別の証明の正しさを証明するために使用できることを意味する。この論文で提示されるシナリオは、潜在的に長い計算結果の正しさを証明したい証明者を含む。チューリング機械があれば、状態遷移関数の個々のステップの正しさを証明できるが、それだけでは不十分である。

Incrementally Verifiable Computing (IVC) の背後にある考え方は次のとおりです。そして、2つの証明を1つにまとめることができます：証明者は、2つの有効な証明を知っていることを示します。jzYM2ARzBX4alsUwhbttZLWhK6b7734TwMiGcppC.jpeg">

結合された証明は、S1からS3への転送が正しいことを証明者に納得させる。このプロセスは任意のステップ数で繰り返すことができるため、任意に長い計算を単一の証明（より具体的には、多項式に長い計算）に圧縮することができる。

この構成は2つの重要な仮定に依存していることに注意することが重要です：

証明システムの知識的健全性：証明者は個々の状態遷移に対する証明の存在を証明するだけでなく、これらの証明を知っていることも証明しなければならない。直感的には、帰納的知識抽出可能性によって、個々の状態遷移のすべての証明を抽出することができる。
Hash functions in practice are random predicators: これはより強い仮定です。しかし、集約証明におけるニュートロソフィーの証明の正しさを検証するために必要です。

この構成は理論的には強力ですが、実際に適用するにはコストがかかります。この問題を解決するために、効率を向上させる新しいアプローチが提案されている。その一つは、仮定を緩和し、再帰的なSNARK検証の必要性を回避するフォールディング・スキーム[^22]の使用である。フォールディングの考え方は、2つの証明πとπ′があれば、それらを1つの証明 π″に「フォールディング」できるというものである。検証者は、折り畳まれたインスタンスが充足可能であれば、元のインスタンスも充足可能であると考える。

10 - zkVMによる検証可能な計算

Ben-Sasson, Chiesa, Tromer, Ben-Sasson, and others.この論文では、ゼロ知識仮想マシン(zkVM)(zkVM)(zkVM)(zkVM)(zkVM)(zkVM)(zkVM)について議論しています。 (zkVM)の構築について論じる。zkVMは、任意のプログラムを実行し、その計算の正しさの証明を生成することができる仮想マシンである。このマシンはフォン・ノイマン・アーキテクチャに従っており、プログラムとデータは同じメモリに格納される。理論的には、古典的なコンピュータで実行可能なプログラムはすべて、このアーキテクチャでも実行可能である。

この論文では、vnTinyRAMと呼ばれるRISCアーキテクチャについて説明し、この命令セットに移植されたCコンパイラを示している。証明システムは、一定ステップ数までのプログラム実行の正しさを検証するように設計されている。基本的な考え方は、回路は命令数の上限に達するまで展開される繰り返し状態遷移関数として構成されるというものである。

今日、zkVMはますます人気が高まっています。その主な利点の1つは、ユーザーが高レベル・プログラミング言語でプログラムを書くことができ、それを使って証明を生成できることです。これは、手作業で回路を書くのに比べて大きな利点となる。多くの標準的なアルゴリズムやデータ構造は、すでにこれらの高級言語で定義されているからだ。さらに、開発者は使い慣れた計算モデルを再利用できるため、ゼロ知識証明を使用する際の学習曲線が大幅に短縮されます。

多くのzk-rollupがこのモデルに基づいていることも注目に値します。たとえば、イーサネット仮想マシン（EVM）実行をサポートするzk-rollupは、zkVMを使用してEVM実行の正しさを証明しています。

最後に、この論文では、ゼロ知識証明システムでの使用に最適化された独自のアーキテクチャについて説明しています。zkフレンドリーなアーキテクチャのもう一つの有名な例は、Cairo CPU architecture [^24]であり、STARKを使った証明のために最適化されたチューリング完全CPUです。

参考論文

[^1]: Goldwasser, S., Micali, S., &; Rackoff, C. ([1985]).1985). (リンク) ︎

[^2].Fiat, A., & Shamir, A. (1986). (リンク) ︎
[^3]: Goldreich, O., Micali, S., & Wigderson, A.(1987). (リンク) ︎
[^4]: Ben-Or, M., Goldreich, O ..、Goldwasser, S.、Håstad, J.、Kilian, J.、Micali, S.、& Rogaway, P. (1990). (リンク) ︎
[^5]: Shamir, A. (1992). IP=PSPACE. (link) ︎
[^6]: Micali, S. (2000). Computationally sound proofs. ([link] (https://people.csail.mit.edu/silvio/Selected Scientific Papers/Proof Systems/Computationally_Sound_Proofs.pdf)) ︎
[^7]: Cook, S. A. (1971). (リンク) ︎
[^8]: Kilian, J. (1992, July). (リンク) ︎
[^9]: Goldwasser, S., Kalai, Y. T., & Rothblum, G. N. (2015). 計算を委譲する：マグルのための対話型証明。 (リンク、Justin Thalerによるこのノートも参照) ︎
[^10]: Lund, C., Fortnow, L., Karloff, H., & Nisan, N. (2015).Amp; Nisan, N. (1992). Algebraic methods for interactive proof systems. (link) ︎
[^11]: Thaler, J. (2015). (リンク) ︎
[^12]: Gennaro, R., Gentry, C., Parno, B., & Raykova, M. (2013). (リンク) ︎
[^13]: Groth, J. (2010). (リンク) ︎
[^14]: Parno, B., Howell, J., Gentry, C., & Raykova, M. (2016). Pinocchio: Nearly practical verifiable computation. (link) ︎
[^15]: Groth,J.(2016)。 (リンク) ︎
[^16]: Sasson, E. B., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer、E., & Virza, M. (2014). Zerocash: Decentralized anonymous payments from bitcoin. (link) ︎
[^17]: Gabizon, A., Williamson, Z. J., & Ciobotaru, O. (2019). (リンク) ︎
[^18]: Kate, A., Zaverucha, G. M., &.Goldberg, I. (2010). (リンク) ︎
[^19]: Ben-Sasson, E., Bentov, I., Horesh, Y., & ; Riabzev, M..(2018). (リンク) ︎
[^20]: Ben-Sasson, E., Bentov, I., Horesh, Y., &.Riabzev, M. (2018). (リンク) ︎
[^21]: Valiant, P. (2008). (リンク) ︎
[^22]: Kothapalli, A., Setty, S., &.Tzialla, I. (2022, August). (リンク) ︎
[^23]: Ben-Sasson, E., Chiesa, A., Tromer, E., & Virza, M. (2014). (リンク) ︎
[^24]: Goldberg, L., Papini, S., & Riabzev, M. (2021). (リンク) ︎