ソラナNFTアプリ「Backpack」がドバイのライセンスを取得した新しい暗号取引所を公開
Solanaブロックチェーン上で動作する有名なNFTウォレットアプリであるBackpackは、今週初めに、近日公開予定の暗号取引所であるBackpack Exchangeに関する重要な発表を行った。
 Jixu
Jixu
著者のツイート @renkingeth
ゼロ知識証明(ZKP) は、分散型台帳技術以来の最も重要な技術革新の1つとしてブロックチェーン分野で広くみなされており、ベンチャーキャピタル投資の主要分野でもある。本稿では、過去40年間のゼロ知識証明技術に関する歴史的文献と最近の研究の両方を体系的にレビューします。
まず、ゼロ知識証明の基本概念と歴史的背景を紹介する。span lang="EN-US">Bulletproofs、Ligeroなどのモデルが、手法の設計、適用、最適化のために使用されている。計算環境の分野では、ZKVM と ZKEVM を紹介し、それらがどのようにトランザクション処理を強化し、プライバシーを保護し、検証効率を改善できるかを探求している。この記事では、Layer 2 拡張ソリューションとしての Zero Knowledge Rollup (ZK Rollup) の動作メカニズムと最適化、およびハードウェア アクセラレーションについても説明します、ハイブリッド・ソリューションや、専用のZK EVMにおける最新の進歩があります。
論文の最後には、ZK コプロセッサ、ZKML、ZKThreads、ZKシャーディング、ZKシャーディング、およびZKシャーディングについて見ていきます。"EN-US">ZKステート Channelsなどの新たなコンセプトが登場し、ブロックチェーンのスケーラビリティ、相互運用性、プライバシー保護の可能性を探っています。
これらの最新技術とトレンドを分析することで、本稿はゼロ知識証明技術の理解と適用に関する包括的な視点を提供し、ブロックチェーンシステムの効率性とセキュリティを強化する大きな可能性を実証し、将来の投資判断に重要な参考資料を提供します。
37
昨今、インターネットは、その普及の一途をたどっている。インターネットがWeb3時代に突入しつつある今日、ブロックチェーンアプリケーション(DApps)は急速に進化しており、毎日のように新しいアプリケーションが登場している。近年、ブロックチェーンプラットフォームは何百万人ものユーザーの活動をホストし、毎日何十億ものトランザクションを処理している。これらの取引は大量のデータを生成し、そのデータにはユーザーの身元、取引金額、口座住所、口座残高などの機密性の高い個人情報が含まれていることが多い。ブロックチェーンのオープンで透明な性質を考えると、この保存されたデータは誰にでも公開され、セキュリティとプライバシーに関する複数の懸念が生じます。
これらの課題に対処する暗号技術には、同型暗号化、リング署名、安全な多人数計算、ゼロ知識証明などがあります。同型暗号化は、暗号文を復号化することなく操作を実行できるようにするもので、口座残高や取引金額の安全性を確保するのに役立つが、口座アドレスの安全性は確保できない。サイクリック署名は、署名者の身元を隠す特殊な電子署名を提供し、口座アドレスを保護するが、口座残高と取引額を保護することはできない。セキュア・マルチパーティ計算では、参加者が他の参加者のデータを知ることなく、計算タスクを複数の参加者に分散させることができ、口座残高と取引額を効果的に保護できるが、やはり口座アドレスは保護できない。さらに、同型暗号化、リング署名、安全な多人数計算を使用して、取引額、口座アドレス、口座残高を明らかにすることなく、ブロックチェーン環境内の証明者が十分な取引額を持っていることを検証することはできない(Sun et al. 2021)。
ゼロ知識証明は、より包括的なソリューションであり、仲介データを明らかにすることなく特定の命題の正しさを検証できる検証プロトコルです(Goldwasser, Micali & Rackoff, 1985) 。このプロトコルは複雑な公開鍵設備を必要とせず、繰り返し実装しても、悪意のあるユーザーが追加の有用な情報にアクセスすることはない(Goldreich, 2004)。ZKPを使用することで、検証者は、私的な取引データを明かすことなく、プ ロヴァーが十分な取引量を持つことを検証することができる。検証プロセスは、証明者が主張する取引額を含む証明書を生成し、その証明書を検証者に渡すことからなり、検証者は証明書に対して事前に定義された計算を実行し、最終的な計算結果を出力して、証明者の声明が受け入れられるか否かを結論づける。プ ロバーの声明が受理されれば、十分な取引額があることを意味する。上記の検証プロセスは、偽造することなくブロックチェーン上に記録することができる(フェージュ、フィアット & Shamir, 1986) 。
ZKPのこの特性により、ブロックチェーン取引と暗号通貨アプリケーションにおいて、特にプライバシーの保護とネットワークのスケーリングの面で中心的な役割を果たすことになり、学術研究の焦点となるだけでなく、分散型台帳技術以来、ブロックチェーン取引で使用される最も重要な技術として広く認識されています。技術-- と、特にビットコイン-- は、分散型台帳技術-- の実装に成功して以来、最も重要な技術革新の一つとして広く認識されている。また、産業への応用やベンチャーキャピタルにとっても重要なトラックである(Konstantopoulos, 2022).
このため、ZkSync や StarkNet, Mina, Filecoin および Aleo などがある。これらのプロジェクトが発展するにつれ、ZKP のアルゴリズム革新が急増し、ほぼ毎週新しいアルゴリズムが報告されています(Lavery, 2024; AdaPulse, 2024)。さらに、ZKP 技術に関連するハードウェア開発は、ZKP に最適化されたチップを含め、急速に進んでいる。例えば、Ingonyama, IrreducibleCysic は大規模な資金調達を完了し、これらの開発はZKP 技術の急速な進歩を示すだけでなく、汎用ハードウェアから特殊ハードウェアへのシフトを反映しています。GPU、FPGA および ASIC ( Ingonyama,
これらの進歩は、ゼロ知識証明技術が暗号技術の分野における重要なブレークスルーであるだけでなく、特に以下の点で、より幅広いブロックチェーン技術アプリケーション- の実現に向けた重要な一歩であることを示しています。プライバシー保護と処理能力の向上- は重要なイネーブラである(Zhou et al, 2022).
その結果、私たちは、将来の投資決定をより良く支援するために、知識ゼロ証明(ZKP) に関する知識を体系的に照合することにしました。この目的のため、ZKPに関する主要な学術論文を包括的にレビューし(関連性と引用数でランク付け)、また、この分野の主要プロジェクトのプロフィールとホワイトペーパーを詳細に分析した(資金調達の規模でランク付け)。これらの包括的なデータ収集と分析は、本稿執筆のための強固な土台となった。
1985年、学者ゴールドヴァッサーは、、Micali、そしてRackoffは、論文The The Knowledge Complexity of Interactive Proof-Systems" という論文で、ゼロ知識証明を最初に提案した。 Proof、ZKP)と対話型知識証明がある。 ゼロ知識、IZK)がある。この論文は、ゼロ知識証明に関する代表的な著作であり、その後の研究に影響を与えた多くの概念を定義している。例えば、知識は"実行不可能な計算(unfeasible computation)として定義される。 computation) output"、すなわち、知識は出力であり、実行不可能な計算でなければならず、単純な関数であってはならず、複雑である必要があることを意味する。実行不可能な計算とは、通常、NP問題、すなわち、解が多項式時間で正しいことを検証できる問題であると理解できます。多項式時間とは、アルゴリズムの実行時間が入力のサイズの多項式関数として表現できることを意味します。これは、コンピュータサイエンスにおいて、アルゴリズムの効率性と実現可能性の重要な尺度である。NP問題は、その解法過程が複雑であるため、計算不可能であると考えられています。しかし、その検証過程は比較的単純であるため、ゼロ知識証明の検証に適しています(Goldwasser、 Micali & Rackoff, 1985 )。
NP問題の古典的な例として、一連の都市を訪問して出発点に戻る最短経路を求める旅行者問題があります。最短経路を見つけるのは難しいかもしれないが,経路が与えられれば,その経路が最短であることを検証するのは比較的簡単である.特定の経路の総距離を検証することは、多項式時間でできるからである。
Goldwasser らは、論文 "knowledge complexity の中で次のように紹介している。EN-US">"」(知識の複雑さ)という概念を導入した。 complexity)という概念で、対話的証明システムにおいて、証明者が検証者に漏らす知識の量を定量化している。また、対話的証明システムという概念も提案した。 ここでは、証明者(Prover)と検証者(Verifier)は、以下のような複数の相互作用を通じて発話を証明する。と検証者(Verifier)は、複数回の相互作用を通じて、与えられた発言の真実性を証明する(Goldwasser、 Micali & Rackoff, 1985 )。
要約すると、Goldwasserらは、ゼロ知識証明の定義を、検証者が検証プロセス中に発話の真理値以外の追加情報を取得しない、特別な種類の対話型証明として要約し、次のように提示しています。
1.completeness: 論証が真であれば、正直な証明者は正直な検証者にこの事実を納得させることができる。
2.reliability (健全性):証明者が文の内容を知らない場合、無視できる程度で検証者を欺くことができる。
3.ゼロ知識:証明プロセスが完了した後、証明者はゼロ知識を得るだけである。span lang="EN-US">"証明者はこの知識を"追加コンテンツにアクセスすることなく所有する(Goldwasser、 Micali & Rackoff, 1985).
ゼロ知識証明とその性質をよりよく理解するために。以下は、セットアップ、チャレンジ、レスポンスの3つのフェーズで、証明者がある個人情報を持っていることを検証する証明の例です。
ステップ1:セットアップ
このステップでは、証明者の目標は、ある秘密の数を知っているという証明を作成することです。s を直接示すことなく、s を証明することです。秘密の数を設定する。
2つの大きな素数 pと qを選び、それらの積を計算する。
計算する。v は証明の一部として検証者に送られるが、検証者や傍観者がs と推論するには不十分である。="EN-US">s.
ランダムな整数 rが選ばれ、計算され、検証者に送られます。この値 xはその後の検証プロセスで使用されるが、ここでも sは公開されない。ランダムな整数を設定し、その結果を計算する。
ステップ2:挑戦(挑戦)
検証者はランダムにビットa(0または1)をランダムに選択し、証明者に送信します。この"挑戦によって、証明者が取るべき次のステップが決定されます。
ステップ3:レスポンス(レスポンス)
プロヴァーが送ったチャレンジに従います。
If, the prover sends (here r is the number he randomly chose earlier).
If , プロヴァーは計算して送信する。a の値に基づいて、プロヴァーが送信したランダムビットが与えられると、プロヴァーは計算する。
最後に、プロヴァーは受信した g に基づいて、.と等しいかどうかを検証する。式が成り立つ場合、検証者は証明を受け入れる。のとき、検証者は計算し、右辺は; を検証する。 "Times New Roman";mso-hansi- mso-bidi-font-family. "Times New Roman"">When the validator calculates バリデータが計算するとき、右側が検証します。
ここで、検証者の計算により、秘密番号s を明かすことなく、証明者が検証プロセスを通過したことが示される。ここで、aは0か1としか取れないので、証明者が運に頼って検証に合格する確率には2つの可能性しかない(aが0を取る場合)。しかし、検証者はその後何度も証明者に挑戦し、証明者は関連する数字を入れ替え続け、検証者に提出し、常に検証をパスすることに成功する。US">sが証明される。この例は、ゼロ知識証明システム(Fiat& Shamir, 1986) の完全性、信頼性、ゼロ知識を示している。
ゼロ知識証明(ZKP) は伝統的に、通常インタラクティブでオンラインであるプロトコルの形で概念化されています。例えば、Sigma プロトコルは通常、認証を完了するために 3 ~ 5 ラウンドの対話を必要とします (Fiat& Shamir, 1986) 。しかし、インスタントトランザクションや投票などのシナリオでは、特にオフラインの検証機能が特に重要なブロックチェーン技術のアプリケーションでは、複数回のやり取りの機会がないことがよくあります(Sunら、2021)。
1988年に、Blum, Feldman, Feldman, Feldman が、NIZKを最初に提案した。US">フェルドマンとミカリは、非対話的ゼロ知識(NIZK)証明の概念を最初に導入し、相互作用の複数のラウンドを必要とせずに、証明者(証明者)と検証者(検証者)が認証プロセスを完了できることを実証した。このブレークスルーにより、即時取引、投票、ブロックチェーン・アプリケーションの実装が実現可能になる(Blum、 Feldman & Micali, 1988)。
彼らは、非対話的ゼロ知識証明(NIZK) が3つの段階に分けられることを提案しました。Setup
2. 計算
3. 検証
3.span>Verification
セットアップフェーズでは、セキュリティパラメータを公開知識(証明者と検証者の両方がアクセス可能)に変換する計算関数を使用します。このようにして、正しいパラメータとアルゴリズムを用いて証明が計算され、検証されるのです。
計算フェーズでは、計算関数、入力、証明キーを使用し、計算結果と証明を出力します。
検証フェーズでは、証明の有効性が証明キーによって検証される。
彼らが提案した公開参照文字列(CRS) モデル、つまり、非対話的なゼロ知識証明のNP 問題に対して、すべての参加者が単一の文字列を共有することに基づいている。知識証明である。このようなモデルの動作は、CRS の信頼された生成に依存しており、すべての参加者が同じ文字列にアクセスできなければならない。このモデルで実装されるスキーマは、CRSが正しく安全に生成された場合にのみ安全である。CRS の生成は、多数の参加者にとって複雑で時間のかかるものである可能性があるため、そのようなスキームのセットアップは、多くの場合使いやすく、証明可能なほどサイズが小さいという事実にもかかわらず、困難である可能性があります(Blum, Feldman &; Mical, 2009)。 Feldman & Micali, 1988).
その後、NIZK 技術は急速な発展を遂げ、対話的なゼロ知識証明を非対話的なものに変換するためのさまざまな方法が出現しました。これらの方法は、システムの構築や基礎となる暗号モデルの前提において様々です。
Fiat-Shamir 変形は、フィアット・シャミール Heurisitc、またはフィアット-シャミールパラダイムとも呼ばれる。フィアットとシャミールのシャミールによる変換。span>の1986は、対話的なゼロ知識証明を非対話的なものに変換できる方法である。この方法は、ハッシュ関数を導入することで対話の回数を減らし、証明の真正性と偽造の困難性を保証するためのセキュリティ仮定に依存している。Fiat-Shamir変換は、ランダム性と相互作用の一部を置き換えるために公開暗号ハッシュ関数を使用し、その出力はある意味でCRSとみなすことができる。このプロトコルは確率的述語機械モデルでは安全であると考えられているが、一様なランダム性と、異なる入力に対するハッシュ関数の出力の独立性の仮定に依存している (Fiat &. Shamir, 1986) 。 Shamir, 1986)である。Canetti、Goldreich、Haleviは、2003 において、次のように述べている。は、この仮定は理論モデルでは正しいが、実際の応用では問題があり、したがって(Canetti、 Goldreich & Halevi, 2003).Micaliは後に、複数のラウンドの相互作用を1つのラウンドに圧縮することによってこの方法を改良し、相互作用プロセスをさらに単純化した (Micali, 1994) (Canetti, Goldreich & Halevi, 2003) 。 1994).
2007年に、Groth、Cramer、
特定の検証者のための非対話的なゼロ知識証明は、特定のアプリケーションシナリオにおける独自の有用価値を示しています。例えば、CramerとShoupが一般化されたハッシュ関数に基づく方法を用いて開発した公開鍵暗号化スキームは、1998と2002で使用されている。"EN-US">2002は選択的暗号文攻撃に効果的に抵抗した。さらに、鍵登録モデルにおいて新しい非対話的なゼロ知識証明法が開発され、すべてのNP 型の問題を解くのに適している。 & Shou, 1998, 2002)。
さらに、Damgård, Fazio, Nicolosiは、既存のFiat-Shamir変換を改良するための新しい方法を2006 に提案し、直接的な相互作用を必要としない非対話的なゼロ知識証明を可能にした。彼らのアプローチでは、証明者はまず、その後の暗号化操作に備えて公開鍵を登録する必要がある。証明者は加法的同形暗号を使用して、知らないうちにデータを操作し、チャレンジに対する応答として答えを含む暗号化メッセージを生成する。このアプローチの安全性は、"複雑さ活用の仮定に基づいています。複雑さ活用の仮定は、難解と考えられているある種の計算問題は、並外れた計算資源を持つ敵対者にとっては解けるかもしれないと主張しています。span lang="EN-US"> (Damgård、 Fazio&Nicolosi、2006)。
Ventre とVisconti in 2009."weak imputable reliability"という概念は、この仮定に代わるものであり、敵対者が偽の証明を提示する際には、それが偽であることを認識していなければならないだけでなく、どのようにしてこの偽の証明を作り出すことに成功したのかについても認識していなければならないことを要求するものである。を認識していなければならない。この要件は、敵が欺く手段を明確にしておかなければならないため、欺くことの難易度を著しく高める。実際には、この概念を使用する敵対者は、指定された証明者の暗号文情報を含む特定の証明を提供する必要があり、それがなければ証明を完成させることは困難であるため、敵対者が証明を偽造しようとしたときにそれを検出することで敵対者の行動を露呈することになる(Ventre and Visconti, 2009)である。
Unruh 変換は、2015 提案された Fiat-Shamir 変換の代替案です。span>転換の代替案である。Fiat-Shamir アプローチは、量子計算の前では一般的に安全ではなく、プロトコルによっては安全でない解が得られることがあります (Unruh, 2015)。span>)。対照的に、Unruh変換は、確率的述語機械モデル(ROM)(NIZK) における任意の相互作用するプロトコルに対して、量子敵対者に対する証明可能な安全性の非対話的なゼロ知識証明を提供します。NIZK)。Fiat-Shamir 法と同様に、Unruh 変換は追加のセットアップステップを必要としない (Ambainis, Rosmanis &;Unruh, 2014)。
また、Kalaiらは、私的情報検索技術に基づく任意の意思決定問題のための議論システムを提案した。このアプローチは、Multi-Provider Interactive Proof System (MIP)モデルを用い、Aielloらの方法によってMIPを議論システムに変換する。この構築は標準模型で動作し、確率的予測子の仮定に依存しない。このアプローチは、"Proofs for Ordinary People (Proofs-for-Muggles) に基づく多くの議論に適用されている。"ゼロ知識論における(Kalai, Raz & Rothblum, 2014)である。
これらの技術を基に、非対話的ゼロ知識証明(NIZK)は、金融取引、電子投票、ブロックチェーン技術など、高度なセキュリティとプライバシー保護を必要とするさまざまなドメインで広く使用されています。相互作用の回数を減らし、証明生成と検証プロセスを最適化することで、NIZK はシステムの効率を向上させるだけでなく、セキュリティとプライバシー保護も強化します。今後、これらの技術がさらに発展・洗練されることで、NIZK がより多くの分野で重要な役割を果たし、より安全で効率的な情報処理・伝送を実現するための強固な技術基盤を提供することが期待される(Partala、 Nguyen & Pirttikangas, 2020)。
暗号の分野では、特に高度な並列化と特定の種類の計算(例えば、大規模な行列演算)を必要とする計算タスクを扱う場合、従来のチューリング・マシン・モデルは、そのような計算タスクに対応するために、次のような問題がありました。伝統的なチューリング機械モデルには限界がある。チューリング機械モデルは、無限に長い紙片をシミュレートするために複雑なメモリ管理機構を必要とし、並列計算やパイプライン演算を直接表現するのには適していません。対照的に、回路モデルは、そのユニークな計算構造の利点を生かし、いくつかの特定の暗号処理タスクに適している( Chaidos、 2017)である。本稿では、回路モジュールに基づくゼロ知識証明システム(ゼロ知識 回路モデルに基づく証明システム)は、計算プロセスを表現し検証するために回路(典型的には算術回路またはブール回路)を使用することに特に重点を置いています。
回路ベースの計算モデルでは、回路は特別な種類の計算モデルとして定義されます。回路ベースの計算モデルでは、回路は、任意の計算プロセスを、特定の論理演算または算術演算を実行する一連のゲートとコネクターに変換できる特別な種類の計算モデルとして定義されます。具体的には、回路モデルは主に2つのカテゴリーに分類されます。
算術回路:主に加算ゲートと乗算ゲートで構成され、有限領域上の要素を処理するために使用されます。算術回路は複雑な数値演算の実行に適しており、暗号アルゴリズムや数値解析に広く使用されています。
論理回路:アンドゲート、オアゲート、ノンゲートなどの基本的な論理ゲートで構成され、ブール演算を処理するために使用されます。論理回路は、単純な判断論理や2進計算を実行するのに適しており、さまざまな種類の制御システムや単純なデータ処理タスクを実装するために一般的に使用される( Chaidos、 2017)と呼ばれています。
ゼロ知識証明システムでは、回路設計のプロセスでは、証明する問題を回路として表現します。zk 回路を設計する必要があるプロセスでは、大量の " 逆の思考が必要になります::"計算の主張された出力が真である場合、出力は特定の要件を満たさなければなりません。これらの要件が足し算や掛け算だけでモデル化するのが難しい場合、これらの要件をより簡単にモデル化できるように、追加の作業を行うよう証明者に依頼する。" 設計プロセスは、通常、次のステップに従います ( Chaidos、 2017):
問題表現:暗号ハッシュ関数の計算過程など、証明すべき問題をまず回路の形に変換する。これには、計算ステップをゲートやコネクタなどの回路の基本単位に分解することが含まれる。
回路の最適化:ゲートマージや定数折りたたみなどの技術により、必要なゲート数や計算ステップ数を減らすことで回路設計を最適化し、システムの動作効率と応答性を向上させます。
多項式表現への変換:ゼロ知識証明技術に対応するため、最適化された回路はさらに多項式形式に変換されます。各回路要素と接続は特定の多項式制約に対応する。
共通参照文字列の生成(CRS): システムの初期化フェーズにおいて、証明キーと検証キーを含む共通参照文字列が生成され、その後の証明生成と検証プロセスで使用される。
証明生成と検証:証明者は回路上で計算を行い、プライベート入力とCRS に基づいてゼロ知識証明を生成する。検証者は、公開されている回路記述とCRS に基づいて、証明の正しさを検証することができる、 2017)である。
ゼロ知識証明回路設計では、特定の計算プロセスを回路表現に変換し、多項式制約を構築することで、追加の個人情報の開示を回避しながら、計算結果が正確であることを保証します。回路設計において重要なタスクは、回路の構造を最適化し、効率的な多項式表現を生成することである。これらのステップを実施することで、ゼロ知識証明技術は、追加情報を開示することなく計算の正しさを検証することができ、プライバシー保護とデータセキュリティという2つのニーズを確実に満たすことができる( Chaidos、 2017)を満たすことができる。
欠点には次のようなものがあります:
1.回路の複雑さとサイズ:複雑な計算には巨大な回路が必要であり、特に大規模なデータを扱う場合、証明の生成と検証の計算コストが大幅に増加します。
2.最適化の難しさ:技術的なツール(ゲートマージ、定数折りたたみなど)により回路の最適化が可能ですが、効率的な回路の設計と最適化は依然として困難です。
4.実装の難しさ:複雑な暗号アルゴリズム(ハッシュ関数や公開鍵暗号など)を実装するには、多数の論理ゲートが必要になる場合があり、回路設計と実装が難しくなります。
5.リソースの消費:大規模な回路は大量のハードウェアリソースを必要とし、消費電力、熱、物理的なスペースの面で、実用的なハードウェア実装のボトルネックになる可能性があります。(Goldreich、 2004; Chaidos,. 2017; Partala, the Nguyen & Pirttikangas, 2020; Sun et al. 2021)。
解決策と改善の方向性:
1.回路圧縮技術:効率的な回路圧縮技術を研究し適用することで、必要な論理ゲートの数と計算リソースを削減する;
2.モジュール設計:モジュール方式で回路を設計することにより、回路設計の再利用性とスケーラビリティを向上させ、異なるタスクのために回路を再設計するのに必要な作業量を削減します。ゼロ知識証明の全体的な性能を向上させる(Goldreich、 2004; Chaidos,. 2017; Partala, the Nguyen & Pirttikangas, 2020; Sun et al. 2021)。
回路ベースのゼロ知識証明は汎用性に乏しく、特定の問題に対する新しいモデルやアルゴリズムの開発が必要であり、既存のさまざまな高級言語が必要である。回路生成や設計アルゴリズムを実行するために、さまざまな高級言語コンパイラや低レベル回路組み合わせツールが存在し、関連する計算の変換は、手動の回路構築ツールまたは自動コンパイラのいずれかで行うことができる。手動変換は通常、より最適化された回路を生成し、自動変換は開発者にとってより便利である。パフォーマンスが重要なアプリケーションでは、多くの場合、手動変換ツールが必要になります(Chaidos、 2017; Partala、 Nguyen & Pirttikangas, 2020; Sun et al, 2021).
この記事では、これらの中で最もよく知られているものについて論じる。集合的に、これらのモデルは zkSNARKs 技術の拡張または亜種であり、それぞれがアプリケーション固有の要件(証明サイズ、計算複雑度、セットアップ要件など)の最適化を提供しようとしています。
各プロトコルには、特にセットアップ要件、証明サイズ、検証速度、計算オーバヘッドの点で、固有の用途、長所、制限があります。これらのプロトコルは、暗号通貨のプライバシーや安全な投票システムから、ゼロ知識方式で検証される一般的な計算まで、様々な領域で使用されている(Čapko、 Vukmirović & Nedić, 2019)。
1.zkSNARKモデル:暗号学者Bitanskyらによって2011年に提案された「ゼロ知識継承モデル」。"Zero-Knowledge Succinct Non-Interactive Knowledge Argument"(ゼロ知識簡潔な非対話的知識論証)(Zero-Knowledge Succinct Non-Interactive Argument of Knowledge)と呼ばれる改良型ゼロ知識証明メカニズムであり、抽出可能衝突耐性ハッシュ(Extractable Collision Resistant Hash:ECRH)関数が存在する場合、NP問題に対するSNARKの実装を可能にし、計算委任、簡潔な非対話型ゼロ知識証明、簡潔な二者間ゼロ知識証明におけるSNARKの有用性を示しています。証明、簡潔な二者間安全計算などにおいてSNARKが有用であることを実証しています。この研究はまた、SNARKの存在がECRHの必要性を示唆しており、これらの暗号プリミティブ間の基礎的なつながりを確立していることも示している (Bitansky ら、2011年)。
zkSNARKシステムは、セットアップ、証明者、検証者の3つの部分から構成される。セットアッププロセスでは、事前に定義されたセキュリティパラメータlとF算術回路Cを用いて、証明鍵(PK)と検証鍵(VK)を生成する。PKは検証可能な証明を生成するために使用され、VKは生成された証明を検証するために使用される。生成されたPKに基づき、証明者は入力x∈Fnと証人W∈Fhを用いて証明pを生成する。 ここで、C(x, W) = 0lである。 n、h、lはそれぞれx、W、Cの出力の次元を表す。最後に、検証者はVK、x、pを用いてpを検証し、検証結果に基づいて証明の可否を決定する (Bitansky ら、2011)。
さらに、zkSNARKにはいくつかの追加機能がある。第一に、検証プロセスは短時間で完了し、証明のサイズは通常数バイトしかない。第二に、証明者と検証者の間で同期通信を行う必要がなく、どの検証者もオフラインで証明を検証できる。最後に、証明者アルゴリズムは多項式時間でのみ実装可能である。それ以来、いくつかの改良されたzkSNARKモデルが登場し、その性能と適用範囲がさらに最適化されている(Bitansky ら、2011)。
2.Ben-Sassonのモデル:Ben-Sassonらは2013年と2014年にvon Neumann RISCアーキテクチャのプログラム実行のための新しいzkSNARKモデルを提案しました。そして、提案された汎用回路生成器に基づいて、Ben-Sassonらはシステムを構築し、プログラム実行の検証への応用を実証した。このシステムは、算術回路の充足可能性を検証する暗号証明システムと、プログラム実行を算術回路に変換する回路生成器の2つのコンポーネントから構成される。この設計は、機能性と効率性、特に回路生成器の汎用性と出力回路サイズの加法依存性の点で先行研究を凌駕している。実験的評価により、本システムは10,000命令までのプログラムを扱うことができ、わずか5ミリ秒の検証時間で高い安全性レベルの簡潔な証明を生成できることが示された。このシステムの価値は、ブロックチェーンやプライバシー保護スマートコントラクトなどの実用的なアプリケーションにzk-SNARKの効率的で一般的かつ安全なソリューションを提供することにある( Ben-Sasson et al., 2013, 2014)。
3.ピノキオモデル:Parnoら(2013)によって提案された、非対話的なゼロ知識論証生成の完全なスイート(Parno et al. al., 2013)。これには高水準コンパイラが含まれており、開発者に計算を回路に変換する簡単な方法を提供する。これらのコンパイラーは高水準言語で書かれたコードを受け入れるため、古いアルゴリズムも新しいアルゴリズムも簡単に変換できる。しかし、適切なサイズの回路を生成するために、コードの構造には制限があるかもしれません。
ピノキオのもう一つの特徴は、四則演算プログラム(QAP)と呼ばれる手法を使用していることです。 QAPは任意の算術回路を多項式の集合として符号化することができ、これらの多項式を生成するのに必要な時間と空間の複雑さは線形である。入出力サイズによって変化しない。Pinocchioが生成する証明のサイズは288バイトであり、計算タスクの複雑さや入出力サイズによって変化することはない。このため、データ転送やストレージのオーバーヘッドが大幅に削減される。Pinocchioの検証時間は通常10ミリ秒であり、これは従来の研究と比べて5~7桁の短縮である。アプリケーションによっては、Pinocchioはローカル実行よりも速い検証速度を達成することさえできます。ワーカーの証明オーバヘッドの削減:Pinocchioは、証明生成にかかるワーカーのオーバヘッドも、従来の研究に比べて19~60分の1に削減します(Parno et al. al., 2013)と比べて19~60分の1に削減されます。
4.防弾モデリング:2017 Benedikt Bünzら(2018)は新しい非対話的ZKPモデルを設計した。Bulletproofsは特に秘密取引における区間証明に適しており、最小数のグループとフィールド要素を用いて、ある値がある範囲内にあることを証明することができる。さらに、Bulletproofsは区間証明の集約をサポートしており、簡潔な複数パーティの計算プロトコルによって1つの証明を生成できるため、通信時間と検証時間が劇的に短縮されます。Bulletproofsは、暗号通貨のような分散したトラストレス環境で効率的かつ有用になるように設計されています。Bulletproofsは伝統的な回路ベースのプロトコルではなく、SNARKよりも簡潔ではなく、Bulletproofの検証にはSNARK証明の検証よりも時間がかかる。しかし、信頼されたセットアップが必要とされないシナリオでは、より効率的です。
5.Ligeroモデル:Amesら(2017)によって提案された軽量なゼロ知識論証モデル。Ligeroの通信複雑度は、検証回路のサイズの平方根に比例する。さらに、Ligeroは任意の衝突耐性ハッシュ関数に依存することができる。さらに、Ligeroは確率的述語モデルにおけるzkSNARKスキームになり得る。このモデルでは、信頼されたセットアップや公開鍵暗号システムを必要としない。Ligeroは非常に大規模な認証回路に使用できる。また、アプリケーションにおける中程度の規模の回路にも適している。
IshaiとPaskin(2007)は、対話的な通信の複雑さを低減するために、加法的同型公開鍵暗号化の使用を提案しました。を提案した。その後Grothらは、離散対数問題とバイリニア対に基づくNIZK方式を提案し、2006年から2008年にかけて発表されたいくつかの研究において、完全な完全性、計算上の正しさ、完全なゼロ知識を達成している。この方式は、ステートメントを代数的制約充足問題として表現し、Pedersenのコミットメントに類似した暗号コミットメント方式を使用することで、Fiat-Shamirヒューリスティックを使用することなく、非線形証明長と非インタラクティビティを実現している。より大きなCRSと「指数関数的知識」という強力な暗号学的仮定が必要であるが、十分に長いCRSは一定の証明長を達成することができる。検証と証明は高価であり、「シミュレートされた抽出可能性」セキュリティモデルが推奨される。 2006, 2008; Groth & Sahai, 2007)。
6.Groth16モデル:2016年にJens Grothによって提案された、効率的な非対話的ゼロ知識証明システムである。このプロトコルは楕円曲線ペアリングとQuadratic Arithmetic Procedure (QAP)に基づいており、簡潔で高速かつ安全なゼロ知識証明を提供することを目的としている 。
7.ソニックモデル:M. Mallerら(2019)によって提案された、多項式コミットメントスキーム、ペアリング、算術回路を用いた、Grothに基づく更新可能なCRSモデル。信頼できるセットアップが必要であり、これは安全なマルチパーティ計算によって実現できる。CRSが生成されると、任意のサイズの回路がサポートされる。
8.PLONKモデル:2019年に提案された一般化されたzk-SNARKであり、ペアリング多項式を用いて算術回路表現を簡略化し、証明をよりシンプルかつ効率的にする、 PLONKモデルは、ソニックの証明の長さを短縮し、証明効率を改善すると主張しているが、まだ査読を受けていない。
9.Marlinモデル:代数的証明システムの効率と、SonicおよびPLONKの汎用的かつ更新可能なセットアップ特性を組み合わせた改良型zk-SNARKプロトコルであり、証明サイズと検証時間の改善を提供する(Chiesa et al. ら、2019)。
10.SLONKモデル:ZacとArielがethresearの論文で紹介した新しいプロトコルで、特定の計算効率の問題に対処し、元のPLONKシステムの機能を強化するために設計されたPLONKの拡張であり、多くの場合、基礎となる暗号の仮定や実装の変更を伴う。(Ethereum Research, 2019)。
11.スーパーソニックモデル:ソニックを信頼できるセットアップを必要としないゼロ知識スキームに変換する、新しい多項式コミットメントスキームのアプリケーション。量子安全ではない(Bünz, Fisch & Szepieniec, 2019)。
「Proofs-for-ordinary-persons」(Proofs-for-Muggles)は、2008年にGoldwasser、Kalai、Rothblumによって提案された新しいゼロ知識証明法である。この方法は、多項式時間証明者のための相互作用証明モデルを、様々な問題に対して構築する。これらの証明は、Kalaiらの変換によって非対話的なゼロ知識証明に変換することができる(Kalai, Raz &. Rothblum, 2014)。
12.Hyraxモデル:コモンマン証明に基づいて、Wahbyら(2018)は最初に、証明者と検証者の両方にとって低コストを実現する、低コミュニケーション、低コストのゼロ知識論証スキームであるHyraxを設計した。この方式では、この論証において信頼できる設定は存在しない。バッチ文に適用した場合、検証時間は算術回路のサイズに良い定数で比例する。証明者の実行時間は、良い定数を持つ算術回路サイズに線形に関係する。非干渉性は離散対数問題に基づくFiat-Shamirヒューリスティックを用いて達成され、反量子セキュリティは達成されない。
13.Libraモデル:線形な証明者時間、簡潔な証明サイズ、検証時間を持つ最初のZKPモデル。Libraでは、検証のオーバーヘッドを削減するために、ゼロ知識メカニズムは、証明者の応答におけるわずかなランダム多項式をマスクできる手法によって実装されている。Libraは漸近的性能に優れ、証明器の効率に優れている。その証明サイズと検証時間の性能も非常に効率的である(Xie et ら、2019)。
証明者アルゴリズムの計算複雑度の点で、LibraはBen-Sassonのモデル、Ligero、Hyrax、Auroraを凌駕する。さらに、Libraの証明者アルゴリズムの計算複雑度は回路の種類に依存しない(Partala、 Nguyen & Pirttikangas, 2020)。
14.スパルタンモデル:Srinath Setty(2019)によって提案されたゼロ知識証明システムであり、信頼できるセットアップを必要とせずに効率的な証明を提供することを目的としている。非干渉性はFiat-Shamir変換を用いて実現される。軽量な設計と大規模な回路を効率的に扱えることで知られている。
Kilian(1992)は、NPのための最初の対話的なゼロ知識論証スキームを構築しました。通信を実装している。このスキームは、衝突に強いハッシュ関数、対話的証明システム(IP)、確率的に検査可能な証明(PCP)を用いる。証明者と検証者は(ランダム化されたアルゴリズムとして)複数のラウンドにわたって通信を行い、検証者は証明者の文に関する知識をテストする。通常、一方的なエラーのみが考慮される。つまり、証明者は常に真の文を守ることができるが、検証者は低い確率で偽の文を受け入れる可能性がある。2000年、MicaliはFiat-Shamir変換を用いて、このスキームをシングルメッセージの非対話型スキームに変換した。以下の実装は、このアプローチを採用していると考えることができる:
15.STARKモデル:2018年、ZK-STARKs (Scalable Transparent ARgument of Knowledge)技法は2018年にBen-Sassonらによって提案され、複雑な証明を扱う際のzk-SNARKsの非効率問題を解決することを目的としている。また、プライベートデータ上の計算の完全性を検証する問題にも対処しており、信頼できるパーティに依存することなく、透明でポスト量子安全な証明を提供することができる。
同年、ベン=サッソンらはスタークウェア・インダストリーズ社を設立。 イーサネットの公式文書によれば、フィアット・シャミール・パラダイムによって確率的述語モデルにおける非干渉性を可能にする。ZK-STARKsはZK-SNARKsと同じ特性を持つが、次のような利点がある:a) スケーラビリティ:認証プロセスがより高速である。プロセスがより速くなります。透明性:認証プロセスは公開される。証明サイズが大きい:高い取引手数料が必要(StarkWare Industries, 2018, 2018)
16.Auroraモデル:Ben-Sassonら(2019)によって提案された、STARKに基づく簡潔な非対話型論証(SNARG)に基づく。非相互作用はFiat-Shamir構成に基づいている。Auroraの引数サイズは、回路サイズとポリ対数的に関連している。さらに、Auroraにはいくつかの魅力的な特徴がある。Auroraでは、透明なセットアップが可能である。さらに、ブラックボックスとして高速対称暗号が使用される。例えば、セキュリティパラメータが128ビットの場合、Auroraの証明サイズは最大250キロバイトです。証明サイズと計算オーバーヘッドを最適化することで、AuroraとLigeroはリソースが限られたデバイスでのゼロ知識証明に適しています。これらの最適化により、効率が向上するだけでなく、ゼロ知識証明技術の範囲が広がり、より実用的なシナリオで使用できるようになります。
17.簡潔オーロラモデル:同論文でBen-Sassonら(2019)が提案:より最適化された証明サイズと検証プロセスを提供するオーロラプロトコルの拡張。Auroraの透過的なセットアップとセキュリティ機能を維持しつつ、効率性を高めている。
18.フラクタルモデル(Fractal model):Chiesaら(2020)によって提案された、効率性とスケーラビリティを向上させるために再帰的な組み合わせを使用する前処理SNARK。対数的な証明サイズと検証時間を利用し、特に複雑な計算に適している。
第一世代(G1)- 各回路には個別の信頼できる設定が必要です。zkSNARK、ピノキオ、および Groth16
ジェネレーション 2 (G2)- は、すべてのサーキットで一度初期設定されます。PlonK、Sonic、Marlin、slonk、および
第3世代 (G3)- 証明システムは、信頼された設定を必要としません。防弾、スパーク、スパルタン、フラクタル、スーパーソニック、リジェロ、オーロラ、そしてフラクタル。簡潔な オーロラ(Čapko, Vukmirović & Nedić, 2019; Partala. Nguyen & Pirttikangas, 2020).
導入の前の部分は、どちらかというとZKP のゼロ知識証明でした。のゼロ知識証明であった。
2019 年に、 Andreevらが"ZkVM。 Fast, Private, Flexible Blockchain Contracts"会議で、ZK-VM のコンセプトがゼロ知識証明システムの実装として初めて紹介された。ZK-VM の目標は、入力データを明らかにすることなくプログラム実行の正しさを検証する仮想マシン プログラムを実行することによって、ゼロ知識証明を生成することです。
VM, (Virtual Machine、(仮想マシン、仮想マシン) は、物理的なコンピュータと同様に、プログラムを実行できるコンピュータ システムのソフトウェア エミュレーションです。仮想マシン は、スタンドアロン オペレーティング システム環境の構築や、ソフトウェアのテストおよび開発などによく使用されます。VM または VM の抽象化は、ほとんどの場合、コンピュータの処理ユニット (CPU) の抽象化を指す CPU の抽象化と同等に理解できます。US">CPU)の複雑な操作とアーキテクチャを、シンプルで相互運用可能な命令セット・アーキテクチャ(ISA)のセットに抽象化することで、コンピュータ・プログラムの設計と実行を簡素化するために使用されます。この抽象化では、コンピュータ プログラムは、実際の CPU の動作挙動を模倣する仮想マシン (VMs) を通して実行できます (Henderson、 2007)を使用しています。
ゼロ知識証明(ZKP) は通常、CPU の抽象化を介して実行する必要があります。セットアップは、証明者が非公開入力上で公開プログラムを実行し、計算の入力や中間状態を明らかにすることなく、プログラムが正しく実行され、主張された出力が生成されることを検証者に証明することを望むというものである。この場合、CPU 抽象化は、証明を生成しながら制御された仮想環境でプログラムを実行できるため有用である(Arun, Setty & Thaler, 2024)。
例:証明者はハッシュ化されたパスワードを明かさずに持っていることを証明したい:
パスワード → ハッシュ関数
非公開 → 公開
一般的に、証明者は以下のことができるはずです。ハッシュ演算を実行するコードを実行し、"proof を生成することで、誰でも証明の正しさ、すなわち、証明者が与えられたハッシュ値の有効な前画像を実際に持っていることを検証できるようにする。
これらのVM 抽象証明を生成するシステムは、しばしば"zkVMs" と呼ばれます。ZKVMs は必ずしもゼロ知識を提供するわけではないので、この名前は実際には誤解を招きやすいものです。要するに、ZKVM はゼロ知識証明に特化した仮想マシンで、従来の VM の機能を拡張して、ゼロ知識回路を開発する障壁を一般的に下げ、あらゆるアプリケーションや計算の証明を即座に生成します。lang="EN-US">(Zhang et al. al., 2023)のための証明を瞬時に生成します。
設計目的に応じて、主に3つのカテゴリーに分けられます。1.メインストリームZKVM
これらのZKVMは、既存の標準命令セット・アーキテクチャ(ISA)とコンパイラー・ツールチェーンを活用し、幅広いアプリケーションと開発環境に対応します。
- RISC Zero(2021年):豊富なコンパイラのエコシステムを備えたRISC-V命令セットを使用(Bögli、 2024).
- ポリゴン Miden(2021年):開発が容易で効率的な標準ベースのISA(Chawla, 2021年)。 2021).
- zkWASM(2022): zkWASMは、広く採用されている標準命令セットであるWebAssembly(WASM)命令セットのゼロ知識証明を実装しています(Delphinus Lab, 2022 )。
2.EVM相当のZKVM
これらのZKVMは、イーサネット仮想マシン(EVM)と互換性があるように特別に設計されており、イーサネット・ バイトコードを直接実行できます。
- zkEVM プロジェクト: いくつかのプロジェクトは、EVM とのバイトコードレベルの互換性を目指しています。 Labs , 2020)やPolygon Hermez(Polygon Labs . 2021).
3.ゼロ知識最適化(ゼロ知識フレンドリー)ZKVM
これらのZKVMは、ゼロ知識証明の効率とパフォーマンスを最適化し、特定のアプリケーションシナリオ向けに設計されています。
- Cairo-VM(2018年):シンプルでSNARK証明と互換性があり、その命令セットは特に算術演算に適した設計となっており、ゼロ知識回路における加算、乗算などの基本的な算術演算の実装を容易にしている(StarkWare、2018年)。
- Valida(2023年):証明生成に必要な計算資源と時間を削減するためにアルゴリズムを最適化するなど、特定の用途向けに最適化されている。軽量設計のため、さまざまなハードウェアおよびソフトウェア環境に適している(Lita Foundation, 2023)。
- TinyRAM (2013): 標準的なツールチェーンに依存しない: 簡素化され最適化された設計のため、通常はLLVMやGCCツールチェーンをサポートせず、小規模なカスタムソフトウェアコンポーネントにのみ使用できる( Ben-Sasson et al.).
一般的な見解は、より単純なVMは、ステップあたりのゲート数がより少ない回路に変換するというものです。これは、TinyRAMやCairo-VMのような、特にシンプルでSNARKフレンドリーなVMの設計に顕著に表れています。しかし、単純なVMに現実のCPUのプリミティブ演算を実装するには多くのプリミティブ命令が必要になるため、これにはさらなるオーバーヘッドが必要になる(Arun, Setty & Thaler, 20)。 & Thaler, 2024)。
プログラミングの観点から、ZKPシステムは一般的に2つの部分に分けられます。一般的に、フロントエンドとバックエンドの2つの部分に分けることができます。ZKPシステムのフロントエンド部分は、主に高レベル言語を表現するために低レベル言語を使用します。">R1CS回路制約構築計算などで表現することができます(たとえば、circomは、R1CSを使用してフロントエンド回路を記述します)。ZKPシステムのバックエンド部分、つまり暗号証明システムは、主に、低レベル言語のフロントエンド構成によって記述された回路を、証明を生成し正しさを検証するための言語に変換します。例えば、バックエンドシステムでよく使われるプロトコルは、Groth16やPlonkなどである(アルン、セッティ & Thaler, 2024; Zhang et al.
通常、回路は、計算手順の各ステップを(信頼されていない " 計算機の助けを借りて)段階的に " 実行します。信頼されていない"提案された入力"の助けを借りて)計算手順の各ステップ。CPUを実行するステップには、概念上、次の 2 つのタスクが含まれます。(1) そのステップのために実行されるべき基本命令を識別すること、および (2) 命令を実行し、を適切に更新すること。lang="EN-US">CPUの状態を適切に更新します。既存のフロントエンドは、慎重に設計されたゲートまたは制約によってこれらのタスクを達成します。これは時間がかかり、エラーが発生しやすく、また、実際に必要とされるよりもはるかに大きな回路になります(Arun, Setty & Thaler, 2024; Zhang et al., 2023)。
長所:
1.既存の ISA を利用する。RISC-VやEVM命令セットなど、既存のコンパイラー・インフラやツールチェーンを活用できるため、インフラをゼロから構築する必要がありません。既存のコンパイラーは、高レベル言語で書かれたウィットネス チェッカーを ISA 用のアセンブリ コードに変換するために直接呼び出すことができ、以前の監査やその他の検証作業の恩恵を受けることができます。
2.単一回路による複数プログラムのサポート: 他のアプローチでは、プログラムごとにフロントエンドを再実行する必要があるかもしれませんが、zkVM では、ある制限時間に達するまで、単一の回路ですべてのプログラムを実行できます。
3.反復構造の回路:フロントエンドは、バックエンドがより高速に処理できる反復構造の回路を出力します(Arun, Setty & Thaler, 2024; Zhang et al.
欠点:
1.一般性によるオーバーヘッド:すべての可能なCPU命令シーケンスをサポートするために、zkVM回路は、その一般性のために支払う必要があり、回路のサイズと証明のコストの増加につながります。
2.高コスト演算:暗号演算など、いくつかの重要な演算をzkVMで実装するには、非常にコストがかかります。たとえば、ECDSA署名検証は実際のCPUで100マイクロ秒かかり、RISC-V命令では数百万命令かかります。そのため、zkVMプロジェクトには、特定の関数を計算するために手作業で最適化された回路とルックアップテーブルが含まれています。
3.証明コストが高い: 非常に単純なISAであっても、既存のzkVMは証明者にとって非常に高価です。例えばCairo-VMの証明では、1ステップごとに51個のドメイン要素を暗号的に投入する必要があります。つまり、生の命令を実行するには実際のCPUで数百万命令を必要とする可能性があり、複雑なアプリケーションへの適用が制限されます(Arun, Setty & Thaler, 20)。 & Thaler, 2024; Zhang et al.
背景ZKEVM(ゼロ知識イーサVM)とZKVM(ゼロ知識仮想マシン)は、どちらもゼロ知識証明(ZKP)技術の仮想マシンへの応用です。技術を仮想マシンに応用したものである。EVM(イーサネット仮想マシン)は、スマートコントラクトのデプロイと実行を処理するイーサネットブロックチェーンシステムの一部です。EVMはスタックベースのアーキテクチャを持ち、特定の命令セット(ロギング操作、実行、メモリとストレージへのアクセス、制御フロー、ロギング、呼び出しなど)に対して計算とストレージを提供するコンピュートエンジンです。EVMの役割は、スマートコントラクトの操作を適用した後にイーサネットの状態を更新することです。ZKEVMはイーサ用に設計されており、主にトランザクションのプライバシーを保護しながらスマートコントラクトの実行の正しさを検証するために使用されます。ZKEVMはEVM命令セットをZKシステムで実行できるように変換し、各命令は状態の証明と実行の正しさの証明を含む証明を提供する必要があります(Čapko、 Vukmirović & Nedić, 2019)。
ZKEVMのより主流なソリューションは、STARKWARE、ZkSync、Polygen-Hermez、Scrollなどである(Čapko、 Vukmirović & Nedić, 2019):
STARKWARE : Ben-Sassonら(2018)によって設立され、STARKゼロ知識証明技術を使用してブロックチェーンのプライバシーとスケーラビリティを改善することに専念している
Polygon-Hermez:もともとは2020年にリリースされた独立したプロジェクトだったが、Hermezは2021年8月にPolygonに買収され、Polygon-Hermezとなった。 高スループットのzk-rollupsソリューションに焦点を当てたHermez。
Scroll:ZhangとPengによって設立された(2021年)Scrollは、より高いトランザクションスループットと低いガス料金を可能にし、全体的なイーサのパフォーマンスとユーザーエクスペリエンスを向上させます。
一般的に、EVMとの互換性のレベルに応じて、EVMは(Čapko. Vukmirović & Nedić, 2019):
1.EVM-EVM互換スマートコントラクト機能レベルの互換性、例えばSTARKWARE、 zkSync
2.EVM-等価性、EVM-コマンドレベルの互換性(等価)、例えばpolygen-Hrmez、scroll
ゼロ知識ベースのイーサネットシステム改善ソリューションについては図1を参照
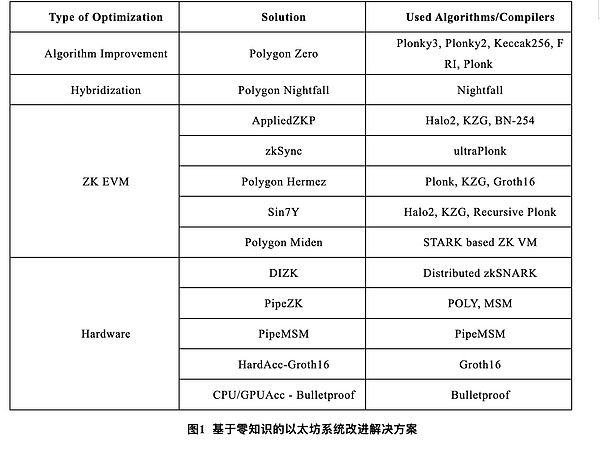
2.その仕組み
ノードプログラムの処理:ノードプログラムは、実行ログ、ブロックヘッダ、トランザクション、コントラクトバイトコード、Merkle証明などを処理および検証し、このデータをzkEVM< /span>に送信します。/span>に送る。
ZK 証明の生成: zkEVM は、zkEVM< /span> の実行結果を生成する回路を使用します。
Solanaブロックチェーン上で動作する有名なNFTウォレットアプリであるBackpackは、今週初めに、近日公開予定の暗号取引所であるBackpack Exchangeに関する重要な発表を行った。
 Jixu
Jixuビットコインが2,100万枚に迫る中、その将来は取引手数料、マイナーのインセンティブ、機関投資家とビットコイン保有者のサポートにかかっている。完全に採掘されたネットワークに向けた進化する複雑な道のりだ。
 Jasper
Jasper中国はNFTに対する姿勢を軟化させており、ブロックチェーン・プロジェクトに対する厳しい規制が1年間続いた後、そのアプローチが顕著に変化したことを示唆する報道がなされている。
 Jixu
Jixuフロリダ州に住む20歳の人物が、暗号通貨のSIMスワップ詐欺に関与し、100万ドル近くを盗んだとして禁固30ヶ月の判決を受けた。
 Jasper
Jasper先週、アクティブなAXSアドレスは3ヶ月ぶりの高値となり、トークン価格は15%以上急騰した。
 Alex
Alexハローキティは誕生50周年を記念して、拡張現実体験、TikTok、ROBLOX、ZEPETOとの連携、全国ツアーなど、グローバルな祭典を開催する。祭りは2023年11月1日に幕を開け、"Friend the Future "をテーマに1年を通してイベントが開催される。世界中のファンは、インタラクティブなARとの出会いやテーマに沿ったコンテンツを楽しむことができる。新しいコスチューム、絵文字、国際的なイベントもこのエキサイティングな祭典の一部です。
 Joy
Joyアリババ、米中AI覇権競争と規制強化の中で「同伊乾文2.0」を発表。
 Hui Xin
Hui Xin米国証券取引委員会(SEC)のゲーリー・ゲンスラー委員長は、ビットコインのホワイトペーパー誕生記念日に祝辞を述べた。ゲンスラーは、サトシ・ナカモトのハロウィーン・コスチュームに戯れを交えつつ、暗号企業に強いメッセージを送り、証券取引法を遵守することの重要性を強調した。
 Jixu
Jixuロシアの国会議員は、登録された企業に対するマイニングの合法化を中心に、民間人の暗号通貨マイニングへの参加禁止を検討している。この動きは、業界の軌跡に影響を与え、産業マイナーの税制を改善するために産業マイニング協会が設立されたことに伴うものである。暗号通貨のロシア経済への統合には時間がかかるかもしれないが、国家間の取引や貿易活動の増加が期待されている。
 Jixu
JixuA42x Ltd.は、シャープ株式会社と共同事業を開始し、「Myna Wallet」の認証・認可インフラを活用して、最先端のユーザー識別システムを開拓します。このエキサイティングなパートナーシップは、シャープ株式会社のAI技術を活用し、ユーザーの本人確認(認証)と認可を可能にし、ユーザーが所有するNFTやその他のデータに基づいて特定のアクションへのアクセスを許可します。
 Joy
Joy