数分で理解する完全同相暗号FHE：動作モードと応用シナリオ

Original Title:Fully Homomorphic Encryption: Introduction and Use-Cases

Original Title.By Nicolas Gama and Sandra Guasch, SandBoxAQ

Compiled by Faust, geekweb3

このブログは、完全同型暗号の体系的な紹介です。ブログは完全同形暗号化（FHE）の体系的な紹介ですが、ここでは数学的な詳細を掘り下げるのではなく、基本的なメカニズム設計の観点から技術を説明し、読者にFHEの基本的な動作ロジックを最初に理解してもらい、FHEの主なアプリケーションモデルをいくつか紹介します。

「暗号化」という用語に言及する場合、まず「暗号化」という言葉が使われます。「暗号化」という言葉を使うとき、最初に思い浮かぶアプリケーションのシナリオは、通常、静止時の暗号化と転送時の暗号化です。前者はデータを暗号化し、ハードドライブ、モバイルデバイス、クラウドベースのサーバーなどのハードウェアデバイスに保存します。一方、転送中の暗号化は、インターネット上で送信されたデータが指定された人物によってのみ解釈されるようにすることを目的としており、たとえデータが公共のルーターやチャネルを介して送信されたとしても、仲介者は平文を私的に復号化することはできません。

これらのシナリオはどちらも暗号化アルゴリズムに依存しており、さらにデータの完全性、つまりデータが送信中に仲介者によって改ざんされていないことを保証するもので、「認証された暗号化」として知られています。いったんデータが暗号化されると、そのデータは指定された人物によってのみ読み取ることができます。これは「認証された暗号化」と呼ばれます:一度データが暗号化されると、データ転送プロセスの参加者は私的に平文を復号化することはできず(機密性)、仲介者は元の暗号文を改ざんすることはできません(完全性/真正性)。

多人数での共同作業シナリオの中には、暗号文の複雑な処理が必要なものがあり、これはプライバシー保護技術のカテゴリーに属します。大統領選挙において、有権者が自分の投票を暗号化して仲介エンティティに提出し、仲介エンティティが統一された方法ですべての投票を収集し、各大統領候補の得票数を計算し、最終的に1つの最終的な選挙結果のみを公表するとします。

残念なことに、先に述べた「認証暗号化」方式を使用する場合、票の集計を担当する仲介機関は、票の集計作業を行うために、全員の投票データの平文を復号化しなければなりません。しかし、これでは全員の投票結果が公開されることになり、プライバシーは保護されない。理論的には、全員の投票データを混ぜてシャッフルすることも可能ですが（一部の電子投票プロトコルはそうしています）、紙の投票とは異なり、従来の暗号メカニズムでは、暗号化された投票データと対応する投票者の身元を分離することは難しく、データの完全性（改ざんされていないこと）を保証することはできません。

オンライン投票のシナリオでは、TEE（Trusted Execution Environment：信頼された実行環境）のようなハードウェアによる隔離の壁を、票の集計を担当する仲介者の周囲に追加することができます。この技術により、悪意のある攻撃者が票数計算プログラムとやりとりすることは難しくなりますが、ハードウェアレベルの脆弱性により、暗号文を解読するための鍵がTEEから漏れてしまう可能性があり、ソフトウェアに含まれるバグとは異なり、ハードウェアの設計上の脆弱性は簡単には修正できません。

要約すると、上記のシナリオに対処するために、完全同相暗号化（FHE）技術を導入することができます。FHEは暗号化スキームの特別な形式で、暗号文を復号化することなく、暗号文に対して関数を直接計算することができ、その関数の出力の暗号化された結果を得ることで、プライバシーを保護します。

FHEのシナリオでは、関数? の数学的構造は一般に公開されているため、入力された暗号文 ? は結果を出力します。(?) の処理フローは公開情報であり、プライバシーを損なうことなくクラウド上で実行できる。ここで重要なのは、? と?(?) はどちらも暗号化された暗号文であり、鍵によって復号化される必要があり、ほとんどの場合どちらも同じ復号化鍵に対応しています。

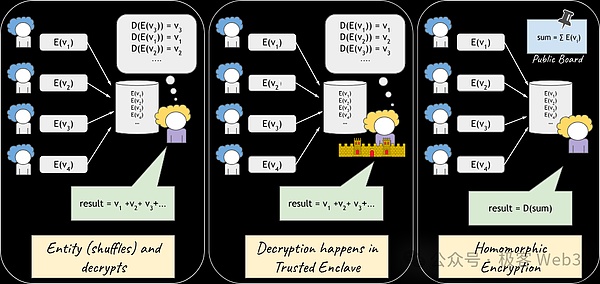
左側の図では、信頼できる仲介者が投票結果を発表する前に個々の投票データを難読化し、復号化しています。

真ん中の図では、TEEが使用されており、データの完全性とプライバシーの保護が保証されています。

真ん中の図では、TEEが使用されており、データの完全性とプライバシーの保護が保証されています。

真ん中の図では、信頼された仲介者が、投票結果を公表する前に、個々の投票データを難読化・復号化しています。left;">そして一番右のグラフでは、同相暗号化が使われています。暗号化された投票データを公開で合計し、復号して最終的な投票数を数える結果を得ることができます

FHE（完全同相暗号化）は、以下のようなコンパクトな暗号化方式です。出力結果?(?) 暗号文データのサイズと、その結果を復号するのに必要な作業量は、元の平文に対応する入力データ? これは、単に? と関数? をソースコードに結合し、受信者がそれを復号して? に入力する。 に入力し、計算タスクを完了させる。

現実には、FHEのアウトソーシングモデルは、しばしばTEEのような安全な実行環境の代替と見なされます。FHEのセキュリティは、暗号アルゴリズムに基づいており、ハードウェアのような物理デバイスに依存していません。その結果、FHE は受動的なサイドチャネル攻撃やクラウドサーバーへの攻撃から完全に保護されます。ある人がコンピューティングタスクをアウトソースする必要があるが、そのデータは非常に機密性が高い場合、そのようなクラウドベースのサーバーの背後には、より高度なコントローラーが存在することが多いため、AWS上に構築された仮想マシン（VM）を使用するのをためらうかもしれません。また、SGXやTEEのようなものを使用するのをためらうかもしれません。なぜなら、TEEを実行しているホストは、計算タスクが実行されるときに生成される消費電力やランタイムなどを監視することができ、そのデータからいくつかの情報を推測することができるからです。

しかし、FHE が使用されれば、コンピューティング タスクをアウトソースする人は安心することができます。というのも、FHEのシステムにある個人情報をクラックするには、FHEが使用している暗号アルゴリズムをクラックしなければならないからだ。

しかし、暗号アルゴリズムは、攻撃者が対応する平文を知らなくても鍵をクラックするのを防ぐことができます。 一方、一般的な拡張性は、攻撃者が出力?(?) 攻撃者は暗号アルゴリズムを実行するハードウェアを標的にして、出力に影響を与えることができる。攻撃者は、出力に影響を与えるために、暗号アルゴリズムを実行するハードウェアをターゲットにすることができます。これは恐ろしく聞こえるかもしれませんが、FHEの設計では、計算フローに冗長性を持たせることで、この種の悪意のある攻撃を回避することができます。

簡単に言うと、FHEは通常、以下を含むいくつかの鍵セットを使用します:

復号鍵:

復号鍵(Decryption)キー): これはFHE暗号化システム全体のマスターキーであり、他のすべてのタイプのキーはマスターキーから導き出すことができる。復号鍵は通常、ユーザーによってローカルに生成され、外部に送信されることはない。つまり、暗号文が転送中に他の誰かに傍受されたとしても、その人が復号鍵を持っていない限り復号することはできない。

暗号化キー: FHEの公開鍵モードでは、暗号化キーは平文を暗号文に変換するために使われるキーです。暗号化鍵は、最初の暗号文を生成した人物が復号鍵/マスター鍵の所持者でない場合に暗号化に使用される。この鍵は通常中程度の大きさで、いくつかのランダムなゼロの暗号化で構成される。FHEはアフィン関数をサポートしているため、あらゆるメッセージを暗号化するのに十分である。

公開鍵暗号化モードでは、暗号化鍵は通常公開され、データを暗号化するために誰でも使うことができますが、復号化鍵の所有者がターゲットとする方法でのみ復号化することができます。

評価キー: 計算キーは、暗号文に対して同型演算を実行するために使用される特別なキーです。 FHEシステムが暗号文を復号化することなく、暗号文に対してホモモルフィック操作を実行することを可能にする、暗号文に対してホモモルフィック操作を実行するために使用される特別な鍵である。 暗号文を復号化することなく？計算鍵は公開鍵と同じように公開することができ、他人が計算鍵を知っていても暗号文を復号化することはできない。 また、暗号文に対して同型演算を行い、出力を得ることしかできません。

さらに、計算鍵で計算する場合、暗号文の構造は変更されず、暗号文に対する同相演算? 同型演算で得られた結果は新しい暗号文に再暗号化されるため、計算プロセスのプライバシーが保証され、計算プロセスが公開されていても機密データが漏れることはありません。

上記の鍵保持者のうち、復号鍵/マスター鍵保持者は最も機密性の高い者であり、、同相演算の実行の連鎖/プロセス全体が効率的でエラーがなく、最終的な暗号文が安全であることを保証し、それを復号して平文の結果を得る。.FHE操作の連鎖の中に悪意のある操作が入り込むと、復号化の際に復号鍵が危険にさらされる可能性がある。しかし幸いなことに、同型演算は公開で実行することができ、誰でも検証することができます。

FHEにおける特定のシナリオ/パターン

このセクションでは、FHEにおけるいくつかの一般的なシナリオ/パターンを説明し、それぞれの利点と欠点について議論します。

アウトソーシング・モード

この図では、左側のオレンジ色の鍵マークが復号鍵（とその保持者であるアリス）を象徴しています。 FHE暗号文は復号鍵と同じ色の鍵で表されています。

ここでは、アリスだけがプライベートなデータを提供する。ボブ側では、同相計算関数と計算鍵は公開されており、緑のボックスで示される計算スキームは決定論的な方法で実行されます。しかし、上記のFHEアルゴリズムのセキュリティは、ハードウェアレベルのセキュリティ対策ではなく、暗号アルゴリズムに基づいています。このセットアップでは、アリスはいくつかのプライベートデータを持っていますが、その計算能力は限られており、ボブは強力な計算能力を持つクラウドサーバーを持っています。

アリスは計算タスク?()の入力パラメータを暗号化して暗号文? を暗号化し、それをBobに送信することができます。Bobはその後、同型暗号化によって、?(?)

FHEアウトソーシングモデルの実用的な展開は、現在のハードウェアデバイスの性能を考えると、遅々として進んでいません。()が非線形の複雑さを持つ場合、FHE演算を実行する?()がFHE演算を実行する場合、元の計算の最大100万倍の時間がかかり、メモリ・オーバーヘッドはおよそ1000倍になる。

現在、FHE アウトソーシング モデルは、実質的に主に PIR (プライベート情報検索) シナリオで使用されています。シナリオでは、パブリック サーバー コントローラーであるボブが大規模なパブリック データベースを所有しており、クライアントであるアリスはデータを読み込むリクエストを開始しますが、ボブがデータを調べたい人について知られることを望んでいません。このタイプのPIRシナリオは、同型暗号操作の線形性とコンパクト性から恩恵を受け、計算コストは合理的な範囲内に抑えることができます。

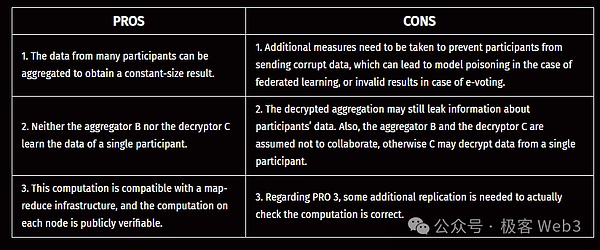
次の表は、FHEアウトソーシングモデルの利点と欠点をまとめたものです。

2者間コンピューティング・モード

グラフは以前と同じ色設定を使用しています。今回、ボブは計算プロセスにプライベートデータを提供する。そして、Bob側の計算フローは、赤枠で示したように、もはや公に検証可能ではありません。このパターンは、通信する両当事者が正直だが好奇心旺盛であるシナリオに限定されるべきです。意図的に間違った結果を出力したり、プロトコルの実行を妨害したりすることはない。しかし、ボブは「好奇心旺盛」であり、出くわした暗号文や他の中間データからできるだけ多くの機密情報を推論しようとしますが、これによってプロトコルの実行が改ざんされることはありません

FHEの2者間計算モデルでは、唯一の違いはボブだけが計算を行うことです。モデルでは、唯一の違いは、ボブが計算プロセスにいくつかのプライベートデータを貢献する、つまり、FHEの計算プロセスに自分のプライベートデータを追加することである。この場合、FHEは通信の複雑さを最小限に抑えた優れた2者間計算ソリューションであり、そのメカニズム設計によって強力な保証を提供することができます：ボブはアリスのプライベートデータを盗み見ることはなく、アリスはボブのプライベートデータを盗み見ることはありません。

このシナリオの潜在的なユースケースの1つは、暗号における「大富豪の問題」です。彼らはどちらが金持ちか知りたいが、もう一方に自分たちがいくら持っているかを正確に知られたくない。この問題の解決策は、実際の電子商取引のシナリオで典型的に使われている。

集約モード

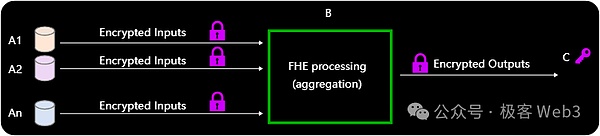
AggregationパターンはOutsourcingパターンを改良したもので、複数の参加者からのデータをコンパクトに（入力パラメータの数に応じて出力が大きくなることはありません）、かつ公に検証可能な方法で集約します。典型的なユースケースには、連合学習やオンライン投票システムなどがあります。

Client-サーバー・モード

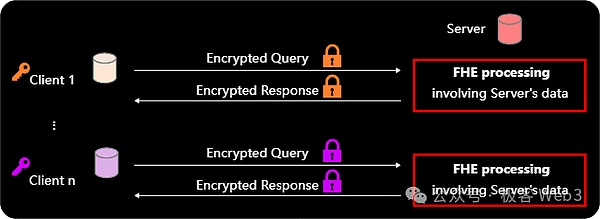
このモードは、サーバー・モードです。align: left;">このモデルは、先に述べた2者間計算モデルを改良したもので、サーバーが独立した鍵を持つ複数のクライアントにFHE計算サービスを提供する。(FHEはプライベートAIモデル計算サービス、例えばプライベートデータとサーバー側のプライベートAIモデルまたはサービスを持つクライアントに使用できる)。サーバーが所有するプライベートAIモデルはローカルに平文で保存され、各クライアントは計算のためにAIモデルに入れたい自分のプライベートデータを持つ。最終的に、各クライアントは自分のキーを使って、自分が提出したデータに対する演算結果を解析することができる。

ホモモーフィック暗号化について その他詳細

同型暗号化はどのようにして外部の計算が有効であることを保証するのですか？

マルチパーティの共同作業シナリオでFHEを使用するのは簡単です。たとえば、FHEは暗号化された計算を実行し、2つの異なる国にありながら同じ企業/組織に属する2つの法人間でいくつかのデータをカウントすることができます。GDPRなどの規制では、特定の統計を外部に公開することは許可されていますが、すべての個人データを同じ物理的な場所に集中的に保存することは禁止されています。

この場合、FHEの使用は実現可能であり、すべての参加者はプロトコルの要件に誠実に従うインセンティブがあります。また、参加者が互いに協力していないシナリオでは、計算タスクが正しく実行されたことを確認する最も簡単な方法は、冗長性を導入することです（マルチ署名/コンセンサスに似ています）。たとえば、先に述べたアウトソーシングや集約のシナリオでは、同形式計算に使用される関数式は完全に公開されており、決定論的であることができます。そのため、2つ以上の独立したエンティティがまったく同じ出力暗号文に到達する限り、計算プロセス全体が正しく、結果は信頼できます。冗長性のレベルが高ければ高いほど、最終的な結果はより信頼できるものになりますが、これには効率性とのトレードオフが必要になります。

さらに、計算タスクを請け負った計算当事者が、入力および出力暗号文にデジタル署名することで、FHE結果の正当性を保証する場合、誰もが同じFHE計算プロセスを再実行し、計算当事者によって与えられた証明が有効かどうかをチェックすることができます。あらゆる計算当事者によるなりすましは検出され、罰せられることができ、なりすましの振る舞いやなりすましを明らかにする、公に検証可能な証明書と関連付けることができる。

完全同型署名に関しては、サードパーティの検証者を必要とせずに計算の正しさを検証する別の方法ですが、一般的に、より多くのハードウェアとソフトウェアのリソースを必要とします。

FHEは、最終的な受信者が最終結果のみを解読し、中間変数は解読しないことをどのように保証するのでしょうか？

最も単純な方法は、復号鍵保持者がFHE計算プロセス中に生成される中間暗号文にアクセスできないようにすることです。2者間計算シナリオまたはクライアントサーバーシナリオでは、アリスが入力結果を暗号化し、ボブが暗号文を計算し、暗号化された出力をアリスに送り返します。

オンライン投票システムのような、多くの参加者がAWSのようなパブリッククラウドサーバー上で暗号化された投票データを送信するクラウドベースのサーバーシナリオでは、次のような手段が使用されます。MPCに似ている）。この場合、特定の暗号文は、多人数で計算を行い、復号鍵を持つメンバー間でオンライン通信を可能にすることによってのみ復号できる。そのうちの何人かが他のメンバーとの協力を拒否した場合、復号化は実行できない。これにより、適切な閾値を設定することで、システム全体のセキュリティが向上します。

Building Blocks for Homomorphic Encryption

Homomorphic Encryptionには、Partial Homomorphic Encryption (PHE)、Graded Homomorphic Encryption (LHE)、Full Homomorphic Encryption (FHE)の3種類があります。完全同相暗号化（FHE）。部分的同相暗号化（Partial Homomorphic Encryption）では、特定の計算タスク（和算、線形関数、双線形関数など）のみを同相暗号化することができますが、段階的同相暗号化（Graded Homomorphic Encryption）と完全同相暗号化（Full Homomorphic Encryption）では、任意の計算タスクをサポートすることができます。

LHEの場合、システムによって使用/生成されるパラメータは、実行される関数計算?()に依存し、その関数の計算複雑度が増すにつれて大きくなり、その結果、暗号文と鍵のサイズが大きくなり、ストレージと通信リソースが消費されます。一方、FHE方式では、与えられたパラメータのセットに対して（つまり、与えられた鍵と暗号文のサイズに対して）、2値論理ゲート回路として表現できる任意の関数を計算することができる。つまり、LHEとは異なり、FHEスキームに関わるパラメータは（鍵と暗号文と同様に）、計算すべきタスクがますます複雑になっても大きくなることはない。

その結果、FHEは、メモリ消費量と同型計算の実行時間の両方が元の平文/タスクに比例することを保証する唯一のモデルです。しかし、FHEには技術的な問題があります。計算が進むにつれて、暗号文に含まれるノイズ（ゴミのようなデータ）が増えていきます。ノイズが多すぎて復号結果がおかしくなるのを防ぐため、FHEスキームは定期的にブートストラッピングと呼ばれるコストのかかる処理を行い、ノイズを扱いやすいレベルまで減らします。これについては、今後詳しく説明しますので、お楽しみに！

Original link: https://cryptographycaffe.sandboxaq.com/posts/fhe-01/