原題:"Exploring circle STARKs" Written by Vitalik Buterin, Co-Founder, Ethereum Compiled by Chris, Techub News
この記事を理解するための前提は、SNARKとSTARKの基本をすでに理解しているということです。
この記事を理解するための前提は、SNARKとSTARKの基本をすでに理解していることです。
近年、STARKsのプロトコル設計のトレンドは、より小さなフィールドに向かっています。STARKs の初期の製品実装では 256 ビットのフィールドを使用していました。.95617)を使用し、楕円曲線ベースの署名と互換性を持たせていた。しかし、この設計は比較的非効率であり、一般的に、このような大きな数の計算を処理する実用的な用途はなく、例えば、(ある数を表す)Xを処理するのと、Xを4倍にするのとでは、計算時間が9分の1にしかならないなど、多くの演算が無駄になります。
このシフトにより、次のような証明のスピードが向上した。Starkwareは、M3のラップトップで1秒間に620,000個のPoseidon2ハッシュを証明することができました。つまり、ハッシュ関数としてPoseidon2を信頼する気になれば、効率的な ZK-EVM の開発における課題を解決できるということだ。では、これらのテクニックはどのように機能するのだろうか?これらの証明はどのように小さなフィールドの上に構築されるのだろうか?これらのプロトコルはBiniusのようなソリューションと比較してどうなのか?この論文では、特に Circle STARKsと呼ばれるスキーム( Starkwareのstwo、Polygonの plonky3 、そしてPythonで実装された私自身のバージョン)に焦点を当てて、これらの詳細を探求する。これはMersenne31フィールドと互換性のあるユニークなプロパティを持ちます。
より小さな数学的場を使用する際によくある問題
ハッシュベースの証明(またはあらゆる種類の証明)を作成する際に非常に重要なトリックは、ランダムな点で多項式の結果を評価することによって多項式を証明することです。多項式の特性を間接的に検証することができる。ランダムな点での評価は通常、多項式全体を扱うよりもはるかに簡単であるため、このアプローチは証明プロセスを大幅に簡略化することができます。
例えば、ある証明システムが、A^3 (x) + x - A (\omega*x) = x^N (ZK-SNARKプロトコルで非常に一般的なタイプの証明)を満たさなければならない多項式Aへのコミットメントを生成するよう求めているとします。プロトコルはランダムな座標? そしてA (r) = cを反転することで、Q = Γ {A - c}{X - r}が多項式であることを証明する。
プロトコルの詳細や内部メカニズムを事前に知っていれば、それを迂回したり破ったりする方法を見つけられるかもしれません。そのための具体的な操作や方法は、次に挙げることができるだろう。例えば、A(Γ*r)の方程式を満たすには、A(r)を0とし、Aを両点を通る直線とすればよい。
このような攻撃を防ぐには、攻撃者がAを与えた後にrを選択する必要があります(Fiat-Shamir は、特定のパラメータを特定のハッシュ値に設定することで攻撃を回避するプロトコルのセキュリティを強化するために使用される技術です)。選択されるパラメータは、攻撃者が予測したり推測したりできないように、十分に大きなセットから選択する必要があります。
楕円曲線ベースのプロトコルや2019年代のSTARKでは、問題は単純です。数学的演算はすべて256ビット数で実行されるため、rを256ビット乱数として選択すれば問題ありません。つまり、証明を改ざんしようとする攻撃者は、20億回試行すればよいのです!
この問題には2つの解決策があります:
複数のランダムチェックを実行する
フィールドを拡張する
複数のランダムチェックを実行する方法は、最も単純で効率的です:1つの座標でチェックする代わりに、4つのランダムな座標でチェックを繰り返します。これは理論的にはうまくいくが、効率性に問題がある。ある値より小さい次数の多項式を扱い、ある程度の大きさの領域で操作している場合、攻撃者は実際に、これらのすべての位置で正常に見える悪意のある多項式を構築することができます。その結果、攻撃者がプロトコルを破れるかどうかは確率的な問題であり、全体的な安全性を高め、攻撃者から効果的に防御できるようにするためには、チェックのラウンド数を増やす必要があります。
このことから、もう一つの解決策である拡張ドメインが導かれます。拡張ドメインは複素数に似ていますが、有限ドメインに基づいています。例えば、α2=some value αα^2 = \text {some value}α2=some valueである。このようにして、有限体上でより複雑な演算を実行できる新しい数学的構造を作り出す。この拡張領域では、乗算の計算は新しい値ααを使った乗算になる。拡張領域では、個々の数値だけでなく、値のペアを操作できるようになった。例えば、MersenneやBabyBearのようなフィールドを扱う場合、このような拡張を行うことで、より幅広い値を選択できるようになり、セキュリティが向上する。フィールドのサイズをさらに大きくするには、同じ技法を何度も繰り返し適用すればよい。すでにααを使ったので、新しい値を定義する必要がある。ααはMersenne31で α2=some value αα^2 = \text {some value}α2=some valueとなるように選択する。align:center">
コード( Karatsuba で改良できます)
ドメインを拡張することで、セキュリティのニーズを満たすのに十分すぎるほどの値から選択できるようになりました。ddd未満の次数の多項式を扱う場合、1ラウンドあたり104ビットのセキュリティを提供できます。これは十分なセキュリティがあることを意味する。より高いレベル、例えば128ビットのセキュリティが必要な場合は、プロトコルに余分な計算を追加してセキュリティを強化することができる。
拡張ドメインは、FRI(Fast Reed-Solomon Interactive)プロトコルや、ランダムな線形結合を必要とする他のシナリオでのみ実用的に使用されます。数学的演算のほとんどは、通常pppまたはqqqのモジュラスのフィールドである基本フィールド上で実行されます。同時に、ハッシュのほとんどすべてがベースフィールド上で行われるため、各値の4バイトだけがハッシュされる必要がある。これは小さなフィールドの効率を利用する一方で、セキュリティの強化が必要な場合にはより大きなフィールドを利用できるようにするものである。
通常のFRI
SNARKやSTARKを構築する際の最初のステップは、通常算術化です。これは任意の計算問題を、ある変数と係数が多項式である方程式に変換することです。具体的には、この方程式は通常P (X,Y,Z) = 0P (X,Y,Z) = 0P (X,Y,Z) = 0のようになります。ここでPは多項式で、X,Y,Zは与えられたパラメータであり、ソルバーはXとYの値を提供する必要があります。このような方程式が利用可能になると、その方程式の解は基礎となる計算問題の解に対応する。
解があることを証明するには、提案している値が確かに妥当な多項式(分数や、ある場所では1つの多項式のように見えて別の場所では異なる多項式などとは異なる)であり、これらの多項式がある最大次数を持つことを示す必要があります。
基本的に、何が起こるかというと、Bが偶数係数Aを分離し、?は奇数の係数を分離します。BとCが与えられれば、元の多項式Aを復元できる:A (x) = B (x^2) + xC (x^2)。もしAの次数が本当に2^{20}より小さければ、BとCの次数はそれぞれAの次数とAの次数から1を引いたものになる。DはBとCのランダムな線形結合なので、Dの次数もAの次数になるはずです。これにより、Dの次数を通してAの次数が条件を満たしていることを検証できます。
まず、FRIは、多項式が次数dを持つことを証明する問題を、多項式が次数 d/2を持つことを証明する問題に還元することで、検証プロセスを単純化する。このプロセスは何度も繰り返すことができ、そのたびに問題は半分に単純化される。
FRI sはこの単純化プロセスを繰り返すことで動作します。例えば、多項式の次数がdであることを証明することから始めると、一連のステップを経て、多項式の次数がd/2であることを証明することになります。ある段階での出力が多項式の次数として期待されるものでない場合、チェックは失敗します。もし誰かが次数dでない多項式をこの手法で押し込もうとすれば、2ラウンド目の出力でその次数が予想と一致しない確率があり、3ラウンド目でも一致しない可能性が高くなり、最終チェックは失敗する。この設計は、不適合な入力を検出して拒否するのに有効である。データセットがほとんどの位置で次数dの多項式に等しい場合、このデータセットはFRI検証に合格する可能性が高い。しかし、そのようなデータセットを構築するためには、攻撃者は実際の多項式を知る必要があるので、少し欠陥のある証明であっても、証明者が「真の」証明を生成できることを示している。
ここで何が起こっているのか、そしてこれをすべて機能させるために必要な性質をより詳しく見てみよう。各ステップで、多項式の数を半分にし、点集合(見ている点の集合)も半分にする。前者はFRI(Fast Reed-Solomon Interactive)プロトコルを機能させるための鍵である。各ラウンドのサイズが前のものと比べて半分になるので、総計算コストはO (N*log (N))ではなくO (N)になります。
領域の段階的縮小を達成するために、2対1の写像が用いられ、各点は2点のうちの1点に写像される。このマッピングにより、データセットのサイズを半分にすることができる。この2対1のマッピングの重要な利点は、繰り返し可能であることである。つまり、このマッピングを適用しても、得られる結果集合は同じ性質を保っている。乗法的な部分群から始めるとしよう。この部分群は集合Sであり、すべての要素xはその倍数2xも集合内に持つ。集合Sを2乗する(つまり、集合の各要素xをx^2にマップする)と、新しい集合S^2は同じ性質を保持する。この操作によって,最終的に1つの値しか残らなくなるまで,データセットのサイズを縮小し続けることができる.理論的にはデータ集合を1つの値だけに減らすことができるが、実際にはより小さな集合に達する前に止めるのが一般的である。
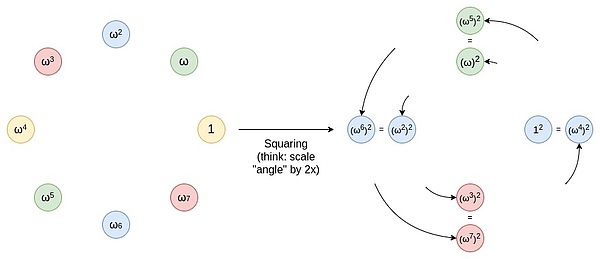
この操作は、ある直線(例えば、線分や円弧)を円の円周上に伸ばし、円の周りを2回転させる処理と考えることができます。例えば、ある点が円周上のx度の位置にある場合、この操作の後、2x度の位置に移動する。円周上の0度から179度までのすべての点に対して、180度から359度の位置に対応する点があり、この2点は一致する。つまり、ある点をx度から2x度に写像すると、x+180度の位置と一致することになる。このプロセスは繰り返すことができる。つまり、このマッピング操作を複数回行い、そのたびに円周上の点を新しい位置に移動させることができる。マッピング技法が効果的であるためには、元の乗法的部分群のサイズを2の大きな累乗で因数分解する必要があります。BabyBearは特定のモジュラスを持つシステムであり、その最大の乗法的部分群がすべての非ゼロ値を含むような値であるため、部分群のサイズは2k-1である(kはモジュラスのビット数)。このサイズの部分群は、マッピング演算を繰り返し適用することで多項式の次数を効果的に下げることができるため、上記のテクニックに適しています。BabyBearでは、サイズ2^kの部分群を選択し(あるいは集合全体を使用し)、FRI法を適用して多項式の次数を段階的に15まで下げ、最後に多項式の次数をチェックすることができます。Mersenne31は、乗法的部分群の大きさが2^31 - 1となるようなある値のモジュラスを持つ別の系である。この場合、乗法的部分群の大きさは2の累乗で因数分解されるだけなので、2で割るのは1回で済む。つまり、BabyBearのように多項式の次数削減のためにFFTを使用することはできません。
メルセンヌ31領域は、既存の32ビットCPU/GPUの演算に適しています。モジュラスの特性(例:2^{31} - 1)により、効率的なビット演算を使用して多くの演算を実行できます。2つの数値を加算した結果がモジュラスを超える場合、結果をモジュラスでシフトすることで適切な範囲に減らすことができます。ビット演算は非常に効率的な演算である。乗算演算では、特定のCPU命令(しばしばハイビットシフト命令と呼ばれる)を使って結果を処理することができる。これらの命令は乗算の上位ビット部分を効率的に計算するため、演算効率が向上する。Mersenne31ドメインでは、上記の特徴により、BabyBearドメインよりも約1.3倍高速に算術演算を行うことができます。FRIをMersenne31ドメインで実装できれば、計算効率が大幅に向上し、FRIの利用がさらに効率的になる。
サークルFRI
これは サークルSTARKs の巧妙さである。を見つけることができる。この母集団は、ある特定の条件、例えば、x^2 mod pがある特定の値に等しい点の集合を満たすすべての点で構成される。
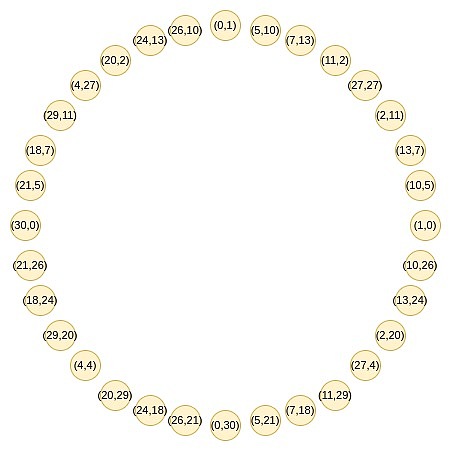
ポイントは、最近三角法や複素数の掛け算に関連したことをしたことがある人なら見覚えがあるかもしれない加法パターンに従います。2 * (x, y) = (2x^2 - 1, 2xy)
さて、この円の奇数位置にある点に注目してみましょう。align:centre">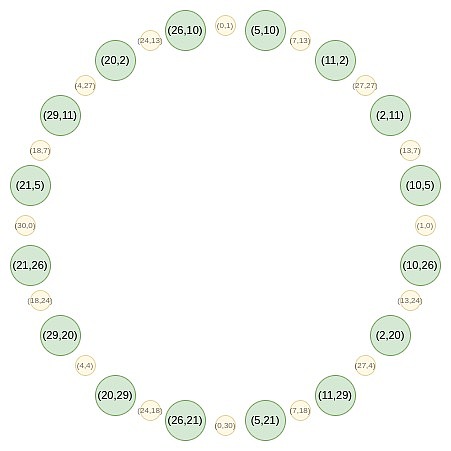
まず、すべての点を直線に収束させます。我々が通常のFRIで使用するB (x²) とC (x²)の等価な公式は:
f_0 (x) = \frac {F (x,y) + F (x,-y)}{2}
次に、1次元のP (x)、x-lineの部分集合上で定義された多項式を得るために、ランダムな線形結合を実行することができます:
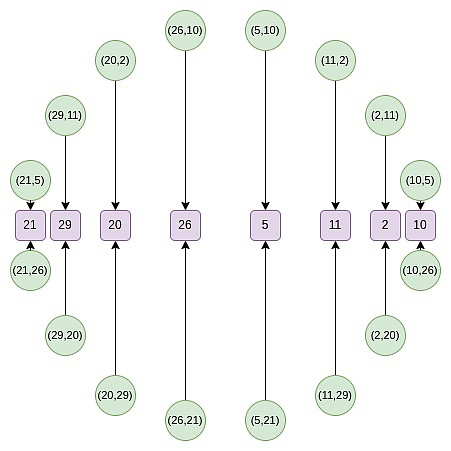
2巡目から、写像が変わります:
f_0 (2x^2-1) = \frac {F (x) + F (-x)}{2}
この写像は実際には毎回上記の集合の大きさを半分にするもので、ここで起こっていることは、各xがある意味で2つの点:(x, y)と(x, -y)を表しているということです。そして、(x → 2x^2 - 1)が上記の点の掛け算の法則である。そこで、円上の対向する2点のx座標を、掛け合わされた点のx座標に変換する。
例えば、円上の右から2番目の点である値2をとり、写像2 → 2 (2^2) - 1 = 7を適用すると、7が得られる。元の円に戻ると、(2, 11)は右から3番目の点なので、これを乗算すると右から6番目の点が得られる。(7, 13).
これは2次元で行うこともできたが、1次元で操作した方が効率的である。
円FFT
FRIと密接に関連するアルゴリズムの1つに FFTがあり、これはn未満の次数の多項式のn回の 評価をその値に変換します。FFTのプロセスはFRIと似ていますが、各ステップでランダムな線形結合 f_0 と f_1を生成する代わりに、FFTはそれらに対して1/2サイズのFFTを再帰的に実行し、FFTの出力(f_0)を偶数係数、FFTの出力(f_1)を奇数係数とします。を奇数係数とします。
サークルグループはFFTもサポートしており、FRIと同様の方法で構築されます。しかし、重要な違いは、サークルFFT(およびサークルFRI)が扱うオブジェクトは厳密には多項式ではないということです。この場合、多項式はモジュロ円(x^2 + y^2 - 1 = 0)である。つまり、x^2 + y^2 - 1の倍数をゼロとして扱う。これを理解する別の方法は、yの累乗しか許さないということである: y^2の項が現れたら、すぐにそれを1 - x^2に置き換える。
これはまた、サークルFFTが出力する係数が、通常のFRIのような単項式ではないことを意味します(例えば、通常のFRIが[6, 2, 8, 3]を出力する場合、これは P (x) = 3x^3 + 8x^2 + 2x + 6を意味することがわかります)。対照的に、円FFTの係数は円FFTの基底に固有である:{1, y, x, xy, 2x^2 - 1, 2x^2y - y, 2x^3 - x, 2x^3y - xy, 8x^4 - 8x^2 + 1...}。
STARKsでは係数を知る必要はありません。STARKsでは、係数を知る必要はありません。その代わりに、多項式を特定の領域で評価された値の集合として保存するだけです。FFTを使う必要があるのは、(リーマン-ロッホ空間のような)低次展開だけです:N個の値が与えられたら、すべて同じ多項式でk*N個の値を生成します。この場合、FFTを使って係数を生成し、それらの係数に(k-1)個のゼロを付加し、逆FFTを使ってより大きな評価値の集合を得ることができます。
円FFTだけが特殊なFFTではありません。FFTはあらゆる有限体(素数体、2進数体など)で動作するため、より強力です。しかし、ECFFTはより複雑で効率が悪いので、 p = 2^{31}-1上で円FFTが使えるので、それを使うことにしました。
ここからは、通常のSTARKとは異なる方法で実装されたCircle STARKを実装するための、より曖昧な詳細に飛び込んでいきます。
商演算
STARKプロトコルで一般的な演算の1つは、特定の点の集合に対して商演算を実行することです。
商を計算する:多項式P (x)と定数yが与えられたら、商Q = {P - y}/{X - x}を計算する。
多項式の証明:Qが分数値ではなく多項式であることを証明する。このようにして、P (x)=y が成り立つことが示される。
さらに、 DEEP-FRIプロトコルでは、メルクル分岐の数を減らすために評価点をランダムに選び、FRIプロトコルの安全性と効率を向上させている。
円グループのSTARKプロトコルを扱う場合、1つの点を通過できる線形関数は存在しないため、従来の商手法の代わりに別の手法が必要になります。そのため、円群特有の幾何学的特性を利用した新しいアルゴリズムを設計する必要があることが多い。
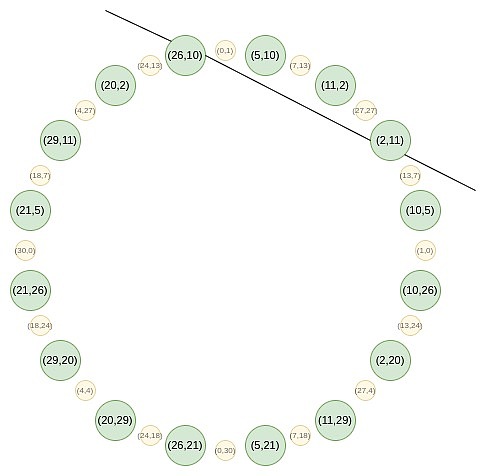
円群では、ある点(P_x, P_y)でその点を切るように接関数を構成することができますが、その関数はその点を通る2の関連性を持つことになります。つまり、多項式がその一次関数の倍数になるためには、単にその点でゼロであることよりも厳しい条件を満たす必要があります。したがって、1点だけでの評価結果を証明することはできない。では、どのように対処すればよいのでしょうか?2点で評価し、注目する必要のないダミーの点を追加することで、この課題を取り上げて証明しなければならない。

Line function: ax + by + c .これを方程式にして、無理やり0に等しくすれば、高校数学で標準形と呼ばれる形の直線として認識できるかもしれません。x_1でy_1、x_2でy_2に等しい多項式Pがあれば、x_1でy_1、x_2でy_2に等しい補間関数Lを選ぶことができます。}{x_2 - x_1} \cdot (x - x_1) + y_1.
次に、Pがx_1においてy_1に等しく、x_2においてy_2に等しいことを、Lを引くことによって証明し(P - Lが両点でゼロになるように)、次にL(すなわち、x_2 - x_1間の線形関数)によりLで割って、商Qが多項式であることを証明する。
消失する多項式
STARKでは、証明しようとする多項式は通常C (P (x), P ({next}(x)) = Zのようになります。(x)・H (x)、ここでZ (x)は元の評価領域全体にわたってゼロに等しい多項式です。通常のSTARKでは、この関数は x^n - 1である。循環STARKでは、対応する関数は:
Z_1 (x,y) = y
Z_2 (x,y) = x
Z_{n+1}(x,y)=(2*Z_n(x,y)^2)-1
折りたたみ関数から消失多項式を導くことができることに注意してください:通常のSTARKでは、x→x^2を再利用します。循環STARKでは、 x → 2x^2 - 1を繰り返す。しかし、最初のラウンドは特別であるため、最初のラウンドについては異なる扱いをします。
逆ビット順序
STARKでは、多項式は通常「自然な」順序では評価されません。(e.g. P (1),P (ω),P (ω2),...,P (ωn-1), but rather in what I call reverse bit order:
P (≖ω≖)。omega^{frac {3n}{8}})
n=16とし、どのωのべき乗で評価するかだけに注目すると、リストは次のようになります:
{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}
この並べ替えは、FRI評価プロセスの早い段階で一緒にグループ化された値が、並べ替えの中で隣り合うという重要な特性を持っています。例えば、FRIの最初のステップでは、 xと -xを一緒にグループ化する。n = 16 の場合、ω^8 = -1であり、P (ω^i) )と( P (-ω^i) = P (ω^{i+8})˶)が成り立つ。FRIの第2段階は、P (ω^i)、P (ω^{i+4})、P (ω^{i+8})、P (ω^{i+12})をグループ化する。これらはまさに、4つのグループで見られるものだ。このようにすることで、FRIはさらにスペース効率が良くなります。なぜなら、一緒に折り畳まれた値(または、一度に k ラウンドを折り畳む場合、すべての2^k個の値)に対して、Merkle証明を提供することができるからです。
サークルSTARKでは、折りたたみの構造が少し異なります:最初のステップでは、(x, y)を (x, -y)と対にし、2番目のステップでは、 xを -xと対にし、その後のステップでは、 pをqと対にし、次に pをqと対にし、次に pをqと対にし、次に pをqと対にします。ここで、 Q^i は x → 2x^2-1 i回繰り返す写像である。これらの点を円周上の位置で考えると、各ステップにおいて、最初の点は最後の点と対になり、2番目の点は最後から2番目の点と対になる。
この折り畳まれた構造を反映するように逆順のビットを調整するには、最後のビットを除くすべてのビットを反転させる必要があります。最後のビットを残し、それを使って他のビットを反転させるかどうかを決めます。
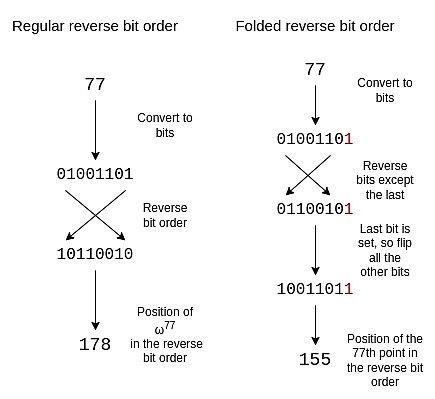
サイズ16の折り畳まれた逆ビットオーダーは以下の通りです:{0, 15, 8, 7, 4, 11, 12, 3, 2, 13, 10, 5, 6, 9, 14, 1}
前節の円を見ると、点0、15、8、7(右から反時計回り)は(x, y)、(x, -y)、(-x, -y)、(-x, y)の形をしており、まさに我々が必要としているものであることがわかる。効率
サークルSTARK(および31ビット素数STARK全般)において、これらのプロトコルは非常に効率的である。
サークルSTARKで証明される計算には、通常いくつかのタイプの計算が含まれます。
1.ネイティブ演算:カウントなどのビジネスロジックに使用されます。
2.ネイティブ演算:暗号化で使用されるもので、例えば Poseidon のようなハッシュ関数です。
3.ルックアップ引数( Lookup arguments):テーブルから値を読み込んで様々な計算を行う汎用的で効率的な方法。
効率の重要な尺度は、有用な作業のためにスペース全体を完全に利用しているか、計算トレースに多くの空きスペースを残しているかです。ビジネスロジックやルックアップテーブルでは、小さな数値(Nは計算の総ステップ数なので、実際には2^{25}未満です)の計算を行うことがよくありますが、それでも2^{256}ビットのフィールドを使用するコストを支払うことになります。この場合、フィールドサイズは2^{31}なので、無駄なスペースは重要ではありません。SNARK用に設計された低演算複雑度のハッシュ(例えばPoseidon)は、どのフィールドのトレースでも、すべての数値のすべてのビットをフルに使用します。
Biniusは、より効率的なビットパッキングを行うために異なるサイズのフィールドを混在させることができ、またBiniusはルックアップテーブルのオーバーヘッドを追加することなく32ビット加算を行うオプションを提供するため、Circle STARKよりも優れたソリューションです。しかし、これらの利点は、サークルSTARK(およびBabyBearベースの通常のSTARK)が概念的にはるかに単純であるのに対して、(私の意見では)より複雑な概念を犠牲にしています。
結論:サークルSTARKについての私の考え
サークルSTARK は、開発者にとってSTARKよりも複雑ではありません。上記の3つの問題は、本質的に、実装時に通常のFRIと異なる点です。サークルFRIが操作する多項式の背後にある数学は非常に複雑であり、数学を理解し理解するのに時間がかかりますが、この複雑さは実際にはあまり目立たない方法で隠されており、開発者が直接感じることはありません。
サークルFRIとサークルFFTを理解することは、他の特殊なFFTを理解する方法でもあります。Binius やその前の LibSTARK で使用されるようなFFT、および少数対多のマッピングを使用し、楕円曲線ポイントワイズ算術でうまく動作する 楕円曲線FFTのような、より複雑な構造です。
Mersenne31、BabyBear、Biniusのようなバイナリードメインテクニックと組み合わせることで、STARKsベースレイヤーの効率性の限界に近づいていると感じています。
ハッシュ関数や署名などの演算効率の最大化:ハッシュ関数やデジタル署名などの基本的な暗号プリミティブを最も効率的な形に最適化することで、STARK証明で使用したときに最高のパフォーマンスを達成できるようにします。パフォーマンスを達成できるようにします。これは、これらのプリミティブを特に最適化して計算を減らし、効率を上げることを意味します。
より多くの並列処理を可能にする再帰的構築:再帰的構築とは、STARK証明プロセスを異なるレイヤーに再帰的に適用することで、並列処理能力を高めることを意味します。こうすることで、計算資源をより効率的に使用し、証明プロセスを高速化することができます。
開発者のエクスペリエンスを向上させるためにVMを算術化する:VMを算術化することで、開発者が計算タスクを作成して実行するのがより効率的で簡単になります。これには、STARK証明で使用するためのVMの最適化が含まれ、スマートコントラクトやその他の計算タスクを構築してテストする際の開発者のエクスペリエンスを向上させます。
 Joy
Joy
 Joy
Joy Clement
Clement Catherine
Catherine Hui Xin
Hui Xin Alex
Alex Jasper
Jasper YouQuan
YouQuan Jixu
Jixu Kikyo
Kikyo Hui Xin
Hui Xin