저자: Arweave Oasis, 출처: PermaDAO
이 글은 논증 과정에서 수학적 추론이 많이 사용되므로 다소 딱딱할 수 있으니 준비하시기 바랍니다. 하지만 수학은 어떤 사물을 논리적으로 설명하는 데 있어 가장 기초적인 학문이라고 생각하기 때문에 @ArweaveEco 메커니즘에서 수학의 아름다움을 간단한 용어로 보여드리려고 노력해 보겠습니다.
백서 해석 (II) 기사에서는 백서에서 @ArweaveEco 메커니즘이 어떻게 작동하는지 설명합니다(White Paper Interpretation (II) 기사. ) 기사에서는 모든 참여자가 데이터 세트의 특정 위치에 실제로 데이터를 저장했음을 증명하기 위해 간결한 접근 증명(#SPoA) 게임을 사용하는 방법에 대해 설명했습니다. 이 패턴은 또한 간결한 복제 증명(#SPoRes )이라는 두 번째 게임을 만드는 데 사용될 수 있으며, 이를 통해 증명자는 데이터 전송 및 검증 비용의 일부로 데이터 세트의 크기에 관계없이 특정 수의 데이터 사본을 저장했음을 검증자에게 증명할 수 있습니다.
SPoRes 게임
간결한 복제 증명(SPoRes) 게임은 다음과 같습니다: 앨리스는 자신이 머클리즈의 사본을 n개 저장했다고 주장합니다. 밥은 앨리스가 거짓말을 하지 않는지 확인하고자 합니다. 이를 위해 그는 앨리스에게 난이도 매개변수 d와 무작위로 생성된 시드를 제공하고, 앨리스는 이를 사용해 매초마다 체크포인트를 방출하는 VDF 해시 체인을 생성하여 데이터 세트 내에서 최대 k 개의 SPoA 챌린지를 해제하는 데 사용할 수 있습니다. 이러한 도전 과제에 해당하는 데이터 블록을 패킹할 때마다 앨리스는 해당 SPoA 증명을 구성할 수 있습니다. 그런 다음 이러한 증명을 해시화하여 Bob의 난이도 매개변수 d와 비교합니다. 증명 해시가 d보다 크면 앨리스는 유효한 솔루션을 찾아 해당 증명을 밥에게 보내고, 밥은 무작위 시드를 전송한 후 앨리스의 유효한 증명을 받기까지의 시간을 기록합니다.
난이도 d를 기준으로 한 번의 시도에서 유효한 해를 찾을 확률 p의 식은 다음과 같습니다:
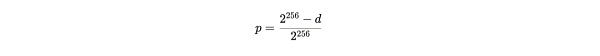
공식 참고: SHA 256 기반 알고리즘은 256비트 문자열이므로 최대 해시 수는 2^256(여기서 "^"는 2의 거듭제곱을 의미)입니다. d보다 큰 유효한 솔루션을 찾으려면 2^256-d 해시만 있으면 되며, 한 번의 시도로 성공 확률을 계산할 수 있습니다.
앨리스가 n개의 복제본을 가지고 있고 복제본당 초당 k번 시도할 수 있는 경우, 주어진 초에 해를 찾을 확률은 다음과 같습니다.

방정식 참고: kN은 앨리스가 1초 동안 해시 해법에 대해 시도할 수 있는 총 횟수를 의미하며, 이것은
위의 두 공식을 대입하여 도출하면 다음과 같이 됩니다.
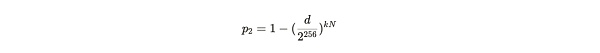
방정식 참고: P2의 방정식에 p를 대입하여 얻은 결과
앨리스가 증명을 제출하는 데 필요한 시간은 기하학적인 무작위 변수 X ~ geom(p2)로 표현할 수 있으며, 여기서 p2는 성공 확률입니다. 이 무작위 변수 X는 d, k, n에 따라 달라집니다. 앨리스가 거짓말을 하고 있는지 확인하기 위해 밥은 앨리스가 120초마다 밥에게 증명서를 제출할 수 있도록 난이도 d를 보내면 앨리스가 복사본을 n개 가지고 있는 경우에만 증명서를 제출할 수 있습니다. 이는 120초 동안 앨리스가 성공할 확률은 다음과 같습니다.
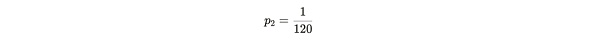
. 방정식 참고: 1/120은 120초에 한 번씩 성공적으로 증명을 제출할 확률입니다
앨리스가 필요한 시간 내에 증명을 제출할 수 있다면, 그녀는 정확한 수의 고유 사본을 가지고 있을 가능성이 높습니다. 그러나 밥이 앨리스가 거짓말을 하지 않는다고 확신하기 위해서는 한 번의 증명만으로는 충분하지 않으며, 앨리스가 오랜 기간 동안 평균 120초마다 계속 증명을 제출할 수 있다면 밥은 앨리스가 원하는 양의 데이터를 저장하고 있다는 것을 합리적으로 확신할 수 있습니다.
다음으로는 앨리스의 저장량에 대한 밥의 확신을 정량화해 보겠습니다.
앨리스가 2주 동안 평균 120초의 속도로 20개의 사본을 보관하고 총 10,080개의 증명을 꾸준히 제출했다고 가정해 보겠습니다. 이 시점에서 밥은 앨리스가 19개(또는 그 이하)의 사본만 보관했다면 이 증명을 제출할 수 있는 확률이 얼마나 될지 궁금합니다. 이는 다른 초에 증명을 제출할 확률에 해당합니다.
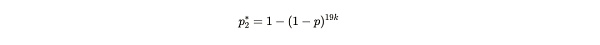
< 방정식 참고: 여기에 표시된 19k는 앨리스가 19개의 복사본을 저장했으며 각 복사본에는 해를 찾기 위한 시도 횟수가 k번 있다는 것을 의미합니다.
간단화:
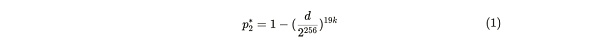
이 확률은 정직한 앨리스에 대해 밥이 생성하는 d-값을 사용하여 계산할 수 있습니다. 앨리스가 19개 이하의 복사본을 저장하는 경우, 앨리스가 1초 안에 증명을 제공할 확률은 아래에서 주어진 일련의 도출을 통해 얻을 수 있습니다. 여기서 p2는 앨리스가 정직하고 20장을 저장하는 경우 1초 안에 증명을 생성할 확률을 나타내고, p2*는 거짓말을 하는 경우(19장 이하 저장) 1초 안에 증명을 제공할 확률을 나타냅니다:

이 유도식은 복잡해 보일 수 있지만 사실 기본적인 수학 능력이 있는 사람이라면 누구나 이해할 수 있는 수식입니다. 파생 과정은 위에서 언급한 회사들의 대체 과정입니다.
따라서 p2*=0.00791832081, 이는 126.2894초의 예상 증명 생성 시간에 해당합니다. X*를 앨리스가 p2*에서 얻은 증명을 제출하는 데 걸리는 시간, 즉 X*~ geom(p2*)이라고 합니다. 이는 복사본이 19개만 저장된 거짓말 케이스에서 앨리스가 증명을 제출하는 데 소요되는 시간 X*의 예상값(평균)을 나타냅니다.
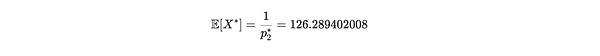
공식 참고: E[X*]는 앨리스가 19부만 저장한 상태에서 증명을 성공적으로 제출하는 평균 시간이 126.2894초라는 것을 의미합니다. 앨리스가 사본을 20개 저장했다면 성공적으로 제출하는 데 걸린 평균 시간은 120초였을 것입니다.
중앙 한계 정리를 사용하여 샘플 평균이 120보다 낮을 확률, 즉 위에서 얻은 기대치 E[X*]와 다를 확률을 추정할 수 있습니다. 이 확률은 다음과 같이 표현됩니다.
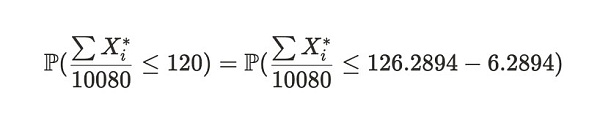
방정식 참고: 방정식의 왼쪽에 있는 식은 2주 동안 Alice가 매번 증명을 제출하는 데 평균 120초 미만이 걸릴 확률을 나타냅니다. 방정식의 오른쪽은 왼쪽의 식을 변형한 것입니다.
샘플 수가 많을 경우 이 부등식의 왼쪽은 평균 E[X*]와 분산 σX*^2/n의 정규 분포로 수렴하며, 여기서 σX*는 Xd의 표준 편차이고 n(여기서 =10,080)은 샘플 크기입니다. 따라서 위의 공식은 다음과 같이 변경할 수 있습니다.
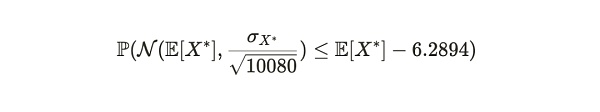
이 분포를 표준 정규분포로 변환할 수 있습니다. 표준 정규 형태로 변환하여 동등한 확률을 얻을 수 있습니다.
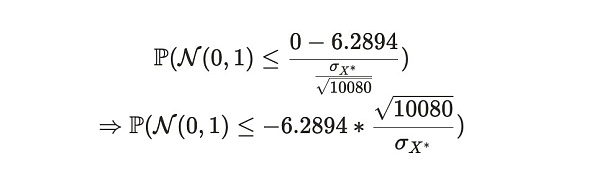
; ">마지막으로, 표준 정규 분포표를 사용하여 앨리스가 이 주간 시간 주기 동안 거짓말을 할 확률을 구할 수 있습니다.
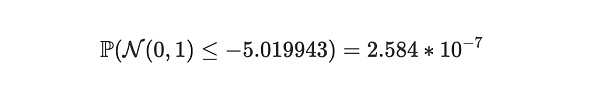
따라서 이 예에서 밥은 2주 동안 앨리스가 데이터 세트의 사본을 19개 이상 저장했다는 것을 약 99.99997416%의 확신으로 판단할 수 있습니다. 만약 앨리스가 19개 미만의 사본을 저장했다면 예상 증명 제출 시간은 126.3초보다 더 길어질 것입니다. 또한 전체 증명 시스템은 120초마다 증명 하나를 전송하면 됩니다. 이는 앨리스와 밥 사이의 평균 데이터 전송 속도인 초당 2.389KB(280KB/120초)로, 비트코인 네트워크의 동기화 오버헤드와 비슷한 수준입니다.
마지막으로, 이러한 확률은 데이터 세트의 크기가 임의로 증가해도 변하지 않으며, 샘플링 기간을 늘리면 밥이 앨리스의 사본 수에 대한 확신의 정확도가 초선형 속도로 계속 향상됩니다(그림 1).
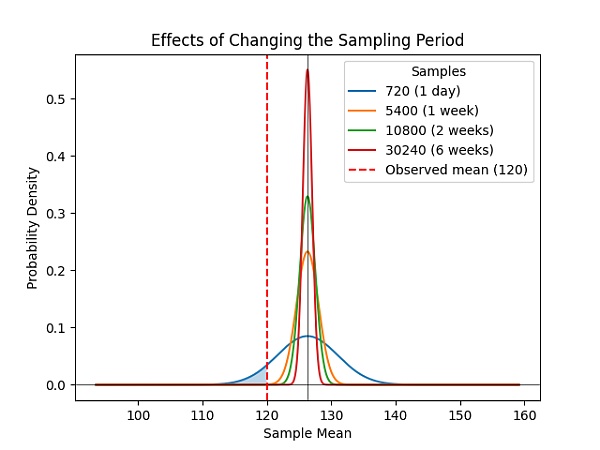
그림 1: 간결한 복제 증명(SPoRes) 게임에서 결정론은 샘플 지속 시간의 증가에 비례하여 초선형적입니다. 2주 동안 샘플을 수집한 후 19개 미만의 복제본을 유지할 확률은 미미합니다(p<0.0000002584).
따라서 SPoRes 게임은 다음 매개변수로 정의됩니다.
위치:
< strong>r= 게임에 사용된 데이터 세트의 메르켈 루트입니다.
k= 사본당 초당 잠금 해제할 수 있는 최대 챌린지 수입니다.
d= 각 시도에서 성공 확률을 결정하는 난이도 파라미터입니다.
이러한 흥미로운 수학적 도출을 통해 채굴자가 합리적인 기간 동안 지속적으로 증명을 제출하는 것만으로 데이터가 저장되고 있는지 여부를 안전하게 확인할 수 있습니다. 이는 탈중앙화된 저장을 목표로 하는 Arweave의 합의 메커니즘의 핵심을 형성합니다. 수학적 재미는 이제 막 시작되었을 뿐이며, 다음 포스팅에서 더 흥미로운 추론과 논증이 이어질 것입니다.
인용 링크
1. Arweave Eco Twitter:
https://twitter.com/@ArweaveEco
2. #SPoA:
https:// twitter.com/search?q=%23SPoA&src=hashtag_click
3. #SPoRes:
https://twitter.com/search?q=%23SPoRes&src=hashtag_click
4. 원본 기사 링크:
p>
https://twitter.com/ArweaveOasis/status/1772089247660638417
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Others
Others Cointelegraph
Cointelegraph