기로에 선 아르헨티나: 지방 화폐의 부상과 새로운 금융 환경
하비에르 밀레이 대통령의 정책으로 인해 라 리오하와 같은 지방에서 자체 화폐 발행을 고려하고 있는 아르헨티나의 경제 상황을 살펴보세요. 이러한 지방 정부의 이니셔티브가 갖는 의미, 로사리오에서 디지털 통화의 혁신적인 사용, 아르헨티나 경제와 글로벌 금융 트렌드에 미치는 광범위한 영향에 대해 자세히 알아보세요.
 Brian
Brian
저자 트윗 @renkingeth
영지식 증명(ZKP)은 블록체인 분야에서 분산원장 기술 이후 가장 중요한 기술 혁신 중 하나로 널리 알려져 있으며 벤처 캐피탈 투자의 핵심 분야이기도 합니다. 이 백서에서는 지난 40년간 영지식 증명 기술에 대한 역사적 문헌과 최근 연구에 대한 체계적인 검토를 제공합니다.
먼저 영지식 증명의 기본 개념과 역사적 배경을 소개합니다. 그런 다음 회로 기반 영지식 증명 기법을 분석하는 데 중점을 두고 zkSNARK, Ben-Sasson, Pinocchio, < span lang="EN-US">Bulletproofs, Ligero 등 다양한 모델을 설계, 적용 및 최적화하는 데 활용하고 있습니다. 컴퓨팅 환경 분야에서는 ZKVM과 ZKEVM을 소개하며 트랜잭션 처리, 개인정보 보호, 검증 효율성을 향상시킬 수 있는 방법을 살펴봅니다. 이 문서에서는 또한 제로 지식 롤업(ZK 롤업ZK EVM의 최신 발전된 기능을 제공합니다.
이 백서는 ZK 코프로세서, ZKML, ZKThreads, ZK 샤딩 및 ZK 상태 채널 등 새롭게 떠오르는 개념들을 살펴보고 블록체인 확장성, 상호운용성, 개인 정보 보호에 대한 잠재력을 살펴봅니다.
이 백서는 이러한 최신 기술과 동향을 분석함으로써 영지식 증명 기술의 이해와 적용에 대한 포괄적인 관점을 제공하고, 블록체인 시스템의 효율성과 보안을 향상시킬 수 있는 큰 잠재력을 보여주며, 향후 투자 결정을 위한 중요한 참고자료를 제공합니다.
37
요즘은 인터넷이 인터넷은 Web3 시대로 접어들고 있으며, 블록체인 애플리케이션(DApps은 거의 매일 새로운 애플리케이션이 등장하면서 빠르게 진화하고 있습니다. 최근 몇 년 동안 블록체인 플랫폼은 수백만 명의 사용자의 활동을 호스팅하고 매일 수십억 건의 트랜잭션을 처리하고 있습니다. 이러한 거래는 사용자 신원, 거래 금액, 계정 주소, 계정 잔액과 같은 민감한 개인 정보를 포함하는 대량의 데이터를 생성합니다. 블록체인의 개방적이고 투명한 특성을 고려할 때, 이렇게 저장된 데이터는 모든 사람에게 공개되므로 여러 보안 및 개인정보 보호 문제가 제기됩니다.
동형 암호화, 링 서명, 안전한 다자간 계산, 영지식 증명 등 이러한 문제를 해결하는 몇 가지 암호화 기술이 있습니다. 동형 암호화를 사용하면 암호문을 해독하지 않고도 작업을 수행할 수 있으므로 계정 잔액과 거래 금액을 보호하는 데 도움이 되지만 계정 주소는 보호하지 못합니다. 순환 서명은 서명자의 신원을 숨기는 특수한 형태의 디지털 서명을 제공하여 계정 주소를 보호하지만 계정 잔액과 거래 금액을 보호하는 데는 아무런 역할을 하지 않습니다. 보안 다자간 계산을 사용하면 어떤 참여자도 다른 참여자의 데이터를 알지 못한 채 계산 작업을 여러 참여자에게 분산할 수 있어 계정 잔액과 거래 금액을 효과적으로 보호할 수 있지만 계정 주소는 보호하지 못합니다. 또한 동형 암호화, 링 서명, 안전한 다자간 계산은 거래 금액, 계정 주소, 계정 잔액을 공개하지 않고는 블록체인 환경에서 증명자가 충분한 거래 금액을 보유하고 있는지 검증하는 데 사용할 수 없습니다(Sun et al. 2021).
영지식 증명은 보다 포괄적인 솔루션으로, 중개 데이터를 공개하지 않고도 특정 명제의 정확성을 검증할 수 있는 검증 프로토콜입니다(Goldwasser, Micali & Rackoff, 1985). 이 프로토콜에는 복잡한 공개 키 시설이 필요하지 않으며, 반복적으로 구현해도 악의적인 사용자에게 유용한 추가 정보에 대한 액세스를 제공하지 않습니다(Goldreich, 2004). ZKP를 사용하면 검증자는 개인 거래 데이터를 공개하지 않고도 증명자가 충분한 거래 금액을 보유하고 있는지 확인할 수 있습니다. 검증 과정은 증명자가 주장하는 거래 금액이 포함된 증명을 생성한 다음 검증자에게 증명을 전달하고, 검증자는 증명에 대해 미리 정의된 계산을 수행한 후 최종 계산을 출력하여 증명자의 진술이 받아들여질지 여부를 결론짓는 것으로 구성됩니다. 증명자의 진술이 수락되면 거래 금액이 충분하다는 것을 의미합니다. 위와 같은 검증 과정은 위변조 없이 블록체인에 기록될 수 있습니다(Feige, Fiat & 샤미르, 1986).
이러한 ZKP의 특성은 블록체인 거래와 암호화폐 애플리케이션에서 특히 개인 정보 보호 및 네트워크 확장 측면에서 중심적인 역할을 하며, 학술 연구의 초점이 될 뿐만 아니라 분산 원장 이후 블록체인 거래에 사용되는 가장 중요한 기술로 널리 인식되고 있습니다. 기술, 특히 비트코인--은 분산 원장 기술이 성공적으로 구현된 이후 가장 중요한 기술 혁신 중 하나로 널리 알려져 있습니다--. 또한 산업 애플리케이션과 벤처 캐피털의 핵심 트랙이기도 합니다(콘스탄토풀로스, 2022).
이것은 ZKP 기반 네트워킹 프로젝트인 ZkSync, StarkNet, Mina, Filecoin 및 Aleo 등이 있습니다. 이러한 프로젝트가 발전함에 따라 ZKP에 대한 알고리즘 혁신이 확산되어 거의 매주 새로운 알고리즘이 보고되고 있습니다(Lavery, 2024; 아다펄스, 2024). 또한, ZKP 기술에 최적화된 칩을 비롯하여 관련 하드웨어 개발이 빠르게 진행되고 있습니다. 예를 들어, 잉고야마, 환원불가능와Cysic은 대규모 자금 조달을 완료했으며, 이러한 개발은 ZKP 기술의 빠른 발전을 보여줄 뿐만 아니라 범용에서 특수 하드웨어로의 전환을 반영하고 있습니다. GPU, FPGA 및 ASIC(잉고야마, 2023; Burger, 2022).
이러한 발전은 영지식 증명 기술이 암호화 분야에서 중요한 돌파구일 뿐만 아니라 특히 다음과 같은 측면에서 더 광범위한 블록체인 기술 애플리케이션을 실현하는 데 중요한 단계임을 보여줍니다-. 개인 정보 보호 및 처리 능력 향상 -은 핵심적인 원동력입니다(Zhou et al, 2022).
그 결과, 향후 투자 결정에 더 나은 도움을 주기 위해 영지식 증명(ZKP)에 대한 지식을 체계적으로 수집하기로 결정했습니다. 이를 위해 관련성 및 인용 횟수에 따라 순위가 매겨진 ZKP 관련 핵심 학술 논문을 종합적으로 검토하고, 해당 분야의 주요 프로젝트의 프로필과 백서(자금 규모에 따라 순위가 매겨진)도 상세하게 분석했습니다. 이러한 포괄적인 데이터 수집과 분석은 이 백서 작성의 탄탄한 토대가 되었습니다.
NP 문제의 대표적인 예로는 일련의 도시를 방문하고 출발점으로 돌아오는 최단 경로를 찾는 '여행자의 문제'가 있습니다. 최단 경로를 찾는 것은 어려울 수 있지만, 경로가 주어지면 그 경로가 최단 경로인지 확인하는 것은 비교적 쉽습니다. 특정 경로의 총 거리를 확인하는 것은 다항식 시간 내에 수행할 수 있기 때문입니다.
Goldwasser 등은 "지식 복잡성을 논문 ""(knowledge 복잡성) 개념을 사용하여 대화형 증명 시스템에서 증명자가 검증자에게 누설하는 지식의 양을 정량화했습니다. 그들은 또한 대화형 증명 시스템, IPS)이라는 개념도 제안했는데, 여기서 증명자(Prover)와 검증자(Verifier)는 발화를 증명합니다. 여러 차례의 상호 작용을 통해 주어진 진술의 진실성을 증명합니다(Goldwasser, 미칼리 & 랙오프, 1985).
요약하면, Goldwasser 등은 영지식 증명을 검증자가 검증 과정에서 발화의 진실 값 이외의 추가 정보를 얻지 못하는 특별한 종류의 대화형 증명으로 정의하고 다음과 같이 제시합니다. 세 가지 기본 속성은 다음과 같습니다 :
1.완전성 : 주장이 참이면 정직한 증명자는 정직한 검증자를 설득 할 수 있습니다. 이 사실에 대한 정직한 검증자;
2.신뢰성 ( 건전성): 증명자가 진술의 내용을 모르는 경우, 그는 검증자를 무시할 수 있는 정도로만 속일 수 있습니다.
3.영지식: 증명 과정이 완료된 후, 증명자는 영지식만 얻게 됩니다. 증명자는 추가 콘텐츠에 대한 액세스 없이 이 지식 "을 보유하게 됩니다(Goldwasser, 미칼리 & 랙오프, 1985).
영지식 증명과 그 속성에 대한 이해를 돕기 위한 예시입니다. 다음은 설정, 챌린지, 응답의 세 단계로 증명자가 일부 개인 정보를 가지고 있는지 확인하는 증명의 예시입니다.
1단계: 설정
이 단계에서는 증명자의 목표는 특정 비밀 번호를 알고 있다는 증명을 만드는 것입니다. s를 직접 보여주지 않고 증명하는 것입니다. 비밀 번호 설정;
두 개의 큰 소수 p와 q를 선택하고 그 곱 을 계산합니다. 계산하여 얻은 소수와 를 설정합니다 ;
계산, 여기서 v가 증명의 일부로 검증자에게 전송되지만 검증자나 방관자가 s.
랜덤 정수 r이 선택되어 계산된 후 검증자에게 전송됩니다. 이 값 x은 후속 확인 프로세스에서 사용되지만 다시 s는 노출되지 않습니다. 임의의 정수를 설정하고 결과 를 계산합니다.
2단계: 챌린지(챌린지)
검증자가 무작위로 비트 a(0 또는 1 중 하나)를 무작위로 선택하여 증명자에게 보냅니다. 이 "챌린지"에 따라 증명자가 수행해야 할 다음 단계가 결정됩니다.
3단계: 응답(응답)
증명자가 보낸 a challenge에 따라 a 값에 따라, 증명자는 다음과 같이 응답합니다.
이 경우, 증명자는 (여기서 r 은 앞서 임의로 선택한 숫자를 전송합니다.)
If 를 증명자가 계산하여 전송합니다. 증명자가 보낸 무작위 비트가 주어지면, 증명자는 a 값을 기반으로 다음을 계산합니다.
마지막으로, 증명자는 수신된 g 를 기반으로 다음 중 와 같은지 확인합니다. 방정식이 맞으면 검증자는 증명을 수락합니다. 검증자는 검증자가 계산하는 를 계산하고, 오른쪽은 ; 검증기가 계산할 때검증기가 계산하면 오른쪽이 유효성을 검사합니다.
여기에서 검증자 계산은 증명자가 자신의 비밀 번호 s를 공개하지 않고 검증 과정을 성공적으로 통과했다는 표시를 산출하는 것을 볼 수 있습니다. 여기서 a는 0 또는 1로만 취할 수 있으므로 증명자가 운에 의존하여 검증을 통과할 확률은 두 가지 가능성만 있습니다(a가 0을 취할 때). 그러나 검증자는 증명자에게 여러 번 도전하고 증명자는 관련 숫자를 계속 바꿔서 검증자에게 제출하고 항상 검증 과정을 통과하는 데 성공하므로 증명자가 운에 의존하여 검증을 통과할 확률(0으로 무한히 수렴)과 증명자가 실제로 어떤 비밀 숫자 s가 증명됩니다. 이 예는 영지식 증명 시스템의 완전성, 신뢰성 및 영지식을 보여줍니다(Fiat& Shamir, 1986).
영지식 증명(ZKP)은 전통적으로 일반적으로 대화형 온라인 프로토콜 형태로 개념화됩니다(예: Sigma). 프로토콜은 일반적으로 인증을 완료하기 위해 3~5회의 상호 작용이 필요합니다(Fiat& Shamir, 1986). 그러나 인스턴트 거래나 투표와 같은 시나리오에서는 여러 차례의 상호작용을 할 기회가 없는 경우가 많으며, 특히 오프라인 유효성 검사 기능이 특히 중요한 블록체인 기술 애플리케이션에서는 더욱 그렇습니다(Sun 외, 2021).
1988년에 Blum, Feldman, Feldman이 최초로 NIZK를 제안했으며, Feldman과 Micali는 비대화형 영지식(NIZK) 증명 개념을 처음 도입하여 여러 차례의 상호작용 없이도 증명자(Prover)와 검증자(Verifier)가 인증 프로세스를 완료할 수 있음을 보여주었습니다. 이러한 혁신을 통해 인스턴트 거래, 투표 및 블록체인 애플리케이션의 구현이 가능해졌습니다 (Blum, Feldman & Micali, 1988).
그들은 비대화형 영지식 증명(NIZK)을 세 단계로 나눌 수 있다고 제안했습니다:
1. 설정
2. 계산
3. 검증
3. 스팬>검증
설정 단계에서는 보안 매개변수를 (증명자와 검증자 모두 액세스할 수 있는) 공개 지식으로 변환하는 계산 함수를 사용하며, 일반적으로 공통 참조 문자열(CRS)로 인코딩합니다. 이것이 올바른 매개변수와 알고리즘을 사용하여 증명을 계산하고 검증하는 방법입니다.
계산 단계에서는 계산 함수, 입력, 증명 키를 사용하고 계산 및 증명 결과를 출력합니다.
검증 단계에서는 증명 키로 증명의 유효성을 검증합니다.
그들이 제안한 공개 참조 문자열(CRS) 모델, 즉 모든 참가자가 비대화형 영점 문제에 대해 단일 문자열을 공유하는 것을 기반으로 하는 NP에 기반한 지식 증명. 이러한 모델의 작동은 모든 참가자가 동일한 문자열에 액세스할 수 있어야 하는 신뢰할 수 있는 CRS 생성에 의존합니다. 이 모델에 따라 구현된 스키마는 CRS가 정확하고 안전하게 생성된 경우에만 안전할 수 있습니다. 많은 수의 참여자에게 CRS의 생성은 복잡하고 시간이 많이 소요될 수 있으므로 이러한 스키마의 설정은 종종 사용하기 쉽고 크기가 작다는 사실에도 불구하고 어려울 수 있습니다(Blum, Feldman & Mical, 2009). Feldman & Micali, 1988).
그 후, NIZK 기술은 대화형 영지식 증명을 비대화형 영지식 증명으로 변환하는 다양한 방법이 등장하면서 빠르게 발전해왔습니다. 이러한 방법은 시스템 구성이나 기본 암호화 모델의 가정에 따라 다릅니다.
Fiat-Shamir 변환, 일명 파이아트-샤미르 변환이라고도 합니다. Heurisitc, 또는 Fiat-Shamir 패러다임; Fiat과 Shamir를 Shamir로 변환한 것입니다. span>은 대화형 영지식 증명을 비대화형 영지식 증명으로 변환할 수 있는 방법입니다. 이 방법은 해시 함수를 도입하여 상호 작용의 수를 줄이고 보안 가정에 의존하여 증명의 신뢰성과 위조 난이도를 보장합니다. Fiat-Shamir 변환은 공개 암호화 해시 함수를 사용하여 일부 무작위성과 상호작용을 대체하며, 그 출력은 어떻게 보면 CRS로 간주할 수 있습니다. 이 프로토콜은 확률적 술어 머신 모델에서 안전한 것으로 간주되지만, 다양한 입력에 대한 해시 함수의 출력의 균일한 무작위성과 독립성을 가정하는 데 의존합니다 (Fiat &. Shamir, 1986). Canetti, Goldreich, Halevi는 2003에서 다음과 같이 제안합니다. 는 이 가정이 이론적 모델에서는 맞지만 실제 적용에서는 문제가 될 수 있으므로 사용 시 실패할 위험이 있다고 제안합니다(Canetti, Goldreich & Halevi, 2003). Micali는 나중에 여러 차례의 상호작용을 단일 라운드로 압축하여 상호작용 프로세스를 더욱 단순화함으로써 이 방법을 개선했습니다(Micali, 1994)(Canetti, Goldreich & Halevi, 2003). 1994).
Jens Groth의 후속 연구는 크게 암호화 및 블록체인 기술에서 영지식 증명의 사용을 크게 발전시켰습니다. 2005에서 그와 오스트로프스키, 사하이가 공동으로 모든 NP에 대한 최초의 영지식 증명을 제안했습니다. ">NP 언어에 완벽한 비대화형 영지식 증명 시스템을 적용하여 동적인 / 적응형 공격에도 보편적인 조합 보안(/)을 보장합니다. 또한, 이들은 수 이론적 복잡성 가정을 사용하여 간결하고 효율적인 비대화형 영지식 증명 시스템을 설계하여 CRS의 크기와 증명의 양을 크게 줄였습니다(Groth & Sahai, 2005).
2007년, Groth, Cramer 및 담가드가 이러한 기술을 상용화하기 시작했고, 이들의 공개 키 암호화 및 서명 체계가 비록 이선형 그룹을 가정하고 있지만 효율성과 보안 모두에서 상당한 개선을 제공한다는 것을 실험적으로 검증했습니다(Groth & Sahai, 2007). span>. 2011에서 Groth는 완전 동형 암호화와 상호 작용하지 않는 영지식 증명을 결합하는 방법을 더 탐구하여 통신 오버헤드를 줄이는 체계를 제안하여 NIZK가 와 일치할 수 있도록 했습니다. span>이 증명의 증인 크기와 일치하도록 하는 방식을 제안했습니다(Groth, 2011). 이후 몇 년 동안 그와 다른 연구자들은 대규모 문에 대해 간결하고 효율적인 비대화형 증명을 제공하기 위해 쌍 기반 기법을 집중적으로 연구했지만, 이러한 증명은 여전히 이선형 그룹 프레임워크 에서 벗어나지 못했습니다(Bayer & Groth,& 2012; Groth, 콜바이스, 핀토레, 2016; 부틀, 세룰리, 차이도스, 그로스, 쁘띠, 2015; 그로스, 오스트로브스키 및 사하이, 2012; 그로스 및 몰러, 2017).
특정 검증자에 대한 비대화형 영지식 증명은 특정 애플리케이션 시나리오에서 고유한 효용 가치를 보여줍니다. 예를 들어, 일반화된 해시 함수에 기반한 방법을 사용하여 Cramer와 Shoup에서 개발한 공개 키 암호화 체계는 1998년과 2002년에 사용되어 왔습니다. "EN-US">2002에서 선택적 암호 텍스트 공격에 효과적으로 저항했습니다. 또한 키 등록 모델에서 새로운 비대화형 영지식 증명 방법이 성공적으로 개발되었는데, 이는 참가자가 후속 검증을 위해 자신의 키를 등록해야 하는 모든 NP 유형 문제를 해결하는 데 적합했습니다(Cramer Shou, 1998, 2002).
또한 Damgård, Fazio, Nicolosi는 2006년에 기존의 Fiat-Shamir 변환을 개선하기 위한 새로운 방법을 제안하여 직접적인 상호 작용 없이 비대화형 영지식 증명을 가능하게 했습니다. 이 접근 방식에서는 증명자가 먼저 후속 암호화 작업에 대비하여 공개 키를 등록해야 합니다. 증명자는 부가적 동형 암호화를 사용하여 무의식적으로 데이터를 연산하여 도전에 대한 응답으로 해답이 포함된 암호화된 메시지를 생성합니다. 이 접근 방식의 보안은 난제로 간주되는 특정 계산 문제가 특별한 계산 리소스를 가진 공격자에게는 풀 수 있다고 주장하는 "복잡성 활용 가정에 기반합니다. span lang="EN-US"> (Damgård, Fazio & Nicolosi, 2006).
Ventre 및 Visconti, 2009. 이 가정에 대한 대안으로, 상대방이 허위 증명을 제시할 때 그 허위성을 인식해야 할 뿐만 아니라 허위 증명을 어떻게 성공했는지도 인식해야 한다는 "약한 전가 가능한 신뢰성" 개념이 있습니다. 어떻게 성공했는지도 알고 있어야 합니다. 이 요건은 상대방이 자신의 속임수 수단을 명확히 알아야 하기 때문에 속임수의 난이도를 크게 높입니다. 실제로 이 개념을 사용하는 공격자는 특정 인증자에 대한 암호 텍스트 정보가 포함된 특정 증명을 제공해야 하며, 이 없이는 증명을 완성하기 어렵기 때문에 증명을 위조하려는 시도를 탐지하여 공격자의 행동을 노출시킬 수 있습니다 (Ventre and Visconti, 2009).
The Unruh 변환은 2015년에 제안된 Fiat-Shamir 변환 대안입니다. 스팬> 변환 대안입니다. Fiat-Shamir 접근 방식은 일반적으로 양자 계산에 직면하면 안전하지 않으며 일부 프로토콜에 대해 안전하지 않은 솔루션을 생성할 수 있습니다(Unruh, 2015). 이와 대조적으로, Unruh 변환은 확률적 술어 기계 모델(ROM)에서 상호작용하는 모든 프로토콜에 대해 양자 공격자에 대해 증명 가능한 보안에 대한 비대화형 영지식 증명을 제공합니다( . NIZK). Fiat-Shamir 방법과 유사하게, Unruh 변환에는 추가 설정 단계가 필요하지 않습니다(Ambainis,& Rosmanis & Unruh, 2014).
또한 Kalai 등은 개인 정보 검색 기법을 기반으로 임의의 의사 결정 문제에 대한 논증 시스템을 제안했습니다. 이 접근 방식은 다중 공급자 대화형 증명 시스템(MIP) 모델을 사용하고 Aiello 등의 방법을 통해 MIP를 논증 시스템으로 변환합니다. 이 구조는 표준 모델에서 작동하며 확률적 예측자 가정에 의존하지 않습니다. 이 접근 방식은 "일반인을 위한 증명(Proofs-for-Muggles)에 기반한 여러 논증에 적용되었습니다. "에서 영지식 인수 (Kalai, Raz & 로스블럼, 2014).
이러한 기술을 바탕으로 금융 거래, 전자 투표, 블록체인 기술 등 높은 수준의 보안과 개인정보 보호가 필요한 다양한 영역에서 비대화형 영지식 증명(NIZK)이 널리 사용되어 왔습니다. 상호 작용 횟수를 줄이고 증명 생성 및 검증 프로세스를 최적화함으로써 NIZK는 시스템 효율성을 개선할 뿐만 아니라 보안과 개인정보 보호도 강화합니다. 앞으로 이러한 기술이 더욱 발전하고 개선됨에 따라 NIZK가 더 많은 분야에서 중요한 역할을 수행하여 더욱 안전하고 효율적인 정보 처리 및 전송을 달성할 수 있는 견고한 기술 기반을 제공할 것으로 기대합니다(Partala, 응우옌 & 피르티칸가스, 2020).
암호화 분야, 특히 고도의 병렬 처리와 특정 유형의 계산(예: 대규모 행렬 연산)이 필요한 계산 작업을 처리하는 경우 기존의 튜링 머신 모델에는 몇 가지 한계가 있습니다. 튜링 머신 모델은 무한히 긴 종이 스트립을 시뮬레이션하기 위해 복잡한 메모리 관리 메커니즘이 필요하며 병렬 연산과 파이프라인 연산을 직접 표현하는 데 적합하지 않습니다. 반면, 회로 모델은 고유한 계산 구조의 장점으로 일부 특정 암호화 처리 작업에 더 적합합니다 (Chaidos, 2017). 이 백서에서는 회로 모듈에 기반한 영지식 증명 시스템(영지식 증명 시스템)에 대해 자세히 살펴봅니다. 회로 모델 기반 증명 시스템)은 계산 프로세스를 표현하고 검증하기 위해 회로(일반적으로 산술 또는 부울 회로)를 사용하는 데 특히 중점을 둡니다.
회로 기반 계산 모델에서 회로는 모든 계산 프로세스를 일련의 계산 프로세스를 특정 논리 또는 산술 연산을 수행하는 일련의 게이트와 커넥터로 변환할 수 있는 특별한 종류의 계산 모델로 정의됩니다. 구체적으로 회로 모델은 크게 두 가지 범주로 나뉩니다.
산술 회로: 유한한 영역에서 요소를 처리하는 데 사용되는 덧셈 및 곱셈 게이트로 주로 구성됩니다. 산술 회로는 복잡한 숫자 연산을 수행하는 데 적합하며 암호화 알고리즘과 수치 해석에 널리 사용됩니다.
논리 회로: 와 게이트 또는 게이트와 같은 기본 논리 게이트와 비 게이트로 구성되며 부울 연산을 처리하는 데 사용됩니다. 논리 회로는 간단한 판단 논리 및 이진 계산을 수행하는 데 적합하며, 다양한 유형의 제어 시스템과 간단한 데이터 처리 작업을 구현하는 데 일반적으로 사용됩니다 ( Chaidos, 2017).
영지식 증명 시스템에서 회로 설계 과정에는 증명할 문제를 하나의 회로로 표현하는 과정으로, zk 회로를 설계하려면 많은 "역발상이 필요합니다. span lang="EN-US">"계산의 주장된 출력이 참인 경우 출력은 특정 요구 사항을 충족해야 합니다. 이러한 요구 사항을 더하기 또는 곱하기만으로 모델링하기 어려운 경우, 증명자에게 추가 작업을 수행하도록 요청하여 이러한 요구 사항을 더 쉽게 모델링할 수 있도록 합니다. " 설계 프로세스는 일반적으로 다음 단계를 따릅니다. ( Chaidos, 2017):
문제 표현: 암호화 해시 함수의 계산 과정과 같이 증명해야 할 문제를 먼저 회로의 형태로 변환합니다. 여기에는 계산 단계를 게이트와 커넥터와 같은 회로의 기본 단위로 분해하는 작업이 포함됩니다.
회로 최적화: 게이트 병합 및 상수 폴딩과 같은 기술을 통해 필요한 게이트 수와 계산 단계를 줄여 회로 설계를 최적화하여 시스템의 운영 효율성과 응답성을 향상시킵니다.
다항식 표현으로 변환: 영지식 증명 기법을 수용하기 위해 최적화된 회로를 다항식 형태로 변환합니다. 각 회로 요소와 연결은 특정 다항식 제약 조건에 해당합니다.
공통 참조 문자열 생성(CRS): 시스템 초기화 단계에서 증명 및 검증 키를 포함한 공통 참조 문자열이 후속 증명 생성 및 검증 프로세스에서 사용할 수 있도록 생성됩니다.
증명 생성 및 검증: 증명자는 회로에서 계산을 수행하여 개인 입력과 CRS를 기반으로 영지식 증명을 생성합니다. 검증자는 증명자의 개인 정보를 알 필요 없이 공개적으로 사용 가능한 회로 설명과 CRS를 기반으로 증명의 정확성을 검증할 수 있습니다 (Chaidos, 2017).
영지식 증명 회로 설계에는 특정 계산 프로세스를 회로 표현으로 변환하고 다항식 제약 조건을 구성하여 계산 결과가 정확하도록 보장하는 동시에 추가적인 개인 정보가 노출되지 않도록 하는 작업이 포함됩니다. 회로 설계에서 핵심 작업은 회로의 구조를 최적화하고 효율적인 다항식 표현을 생성하는 것으로, 이는 증명 생성 및 검증의 효율성을 개선하기 위한 것입니다. 이러한 단계를 구현함으로써 영지식 증명 기법은 추가 정보를 공개하지 않고도 계산의 정확성을 검증할 수 있어 개인정보 보호와 데이터 보안이라는 두 가지 요구 사항을 충족할 수 있습니다 ( Chaidos, 2017).
단점에는 다음이 포함됩니다:
1. 회로 복잡성 및 크기: 복잡한 계산에는 거대한 회로가 필요하므로 특히 대규모 데이터를 다룰 때 증명 생성 및 검증의 계산 비용이 크게 증가합니다.
2. 최적화의 어려움: 기술 도구(예: 게이트 병합, 상수 접기 등)를 통해 회로 최적화가 가능하지만 여전히 효율적인 회로 설계 및 최적화는 어렵습니다. 특정 컴퓨팅 작업에 대한 적응성: 컴퓨팅 작업마다 다른 회로 설계가 필요하며, 각 특정 작업에 맞는 효율적인 회로 설계는 시간이 많이 걸리고 일반화하기 어려울 수 있습니다.
4. 구현의 어려움: 복잡한 암호화 알고리즘(예: 해시 함수 또는 공개 키 암호화)을 구현하려면 많은 수의 논리 게이트가 필요하므로 회로 설계 및 구현이 어려울 수 있습니다.
5. 자원 소비: 대규모 회로에는 많은 양의 하드웨어 리소스가 필요하며 실제 하드웨어 구현 시 전력 소비, 열 및 물리적 공간 측면에서 병목 현상이 발생할 수 있습니다. (Goldreich, 2004; Chaidos,. 2017; Partala, the Nguyen & Pirttikangas, 2020; Sun 외. 2021).
솔루션 및 개선 방향 :
1. 회로 압축 기술: 효율적인 회로 압축 기술을 연구하고 적용하여 필요한 논리 게이트 수와 연산 자원을 줄입니다.
2. 모듈식 설계: 회로를 모듈식으로 설계하여 회로 설계의 재사용성 및 확장성을 개선하고, 다른 작업에 맞게 회로를 재설계하는 데 필요한 작업량을 줄입니다.
3. 하드웨어 가속: 특수 하드웨어(예: FPGA 또는 ASIC)를 사용하여 회로 계산을 가속화하여 다음을 수행합니다. 영지식 증명의 전반적인 성능을 향상시킵니다(Goldreich, 2004; Chaidos,. 2017; Partala, the 응웬 & amp; 피르티캉가스, 2020; 선 외. 2021).
"Times New Roman";;mso-bidi-">배경
회로 기반 영지식 증명은 일반화가 잘 되지 않아 특정 문제에 대한 새로운 모델과 알고리즘을 개발해야 하고 기존의 다양한 고급 언어를 사용해야 합니다. 회로 생성 및 설계 알고리즘을 수행하기 위한 다양한 고급 언어 컴파일러와 저수준 회로 조합 도구가 존재하며, 관련 계산의 변환은 수동 회로 구성 도구 또는 자동 컴파일러를 통해 수행할 수 있습니다. 수동 변환은 일반적으로 더 최적화된 회로를 생성하는 반면, 자동 변환은 개발자에게 더 편리합니다. 성능이 중요한 애플리케이션은 일반적으로 수동 변환 도구가 필요합니다(Chaidos, 2017; Partala, 응우옌 & 피르티칸가스, 2020; 선 외, 2021).
이 문서에서는 이 중 가장 잘 알려진 모델에 대해 설명합니다. 총체적으로 이러한 모델은 zkSNARKs 기술의 확장 또는 변형이며, 각각 애플리케이션별 요구 사항(예: 증명 크기, 계산 복잡성, 설정 요구 사항 등)에 대한 최적화를 제공하려고 시도합니다.
각 프로토콜은 특히 설정 요건, 증명 크기, 검증 속도, 계산 오버헤드 측면에서 고유한 애플리케이션, 강점, 한계를 가지고 있습니다. 이러한 프로토콜은 암호화폐 개인정보 보호 및 보안 투표 시스템부터 영지식 방식으로 검증된 일반 연산에 이르기까지 다양한 영역에서 사용됩니다(Capko, Vukmirović & Nedić, 2019).
1. zkSNARK 모델: 2011년 암호학자 비탄스키 등이 제안한 "영지식 간결한 비대화형 지식 인수" (영지식 간결한 비대화형 지식 인수), 이는 향상된 영지식 증명 메커니즘으로, 추출 가능한 충돌 방지 해시(ECRH) 함수가 존재하는 경우 NP 문제에 대해 SNARK를 구현할 수 있으며, 계산 위임, 간결한 비대화형 영지식 증명, 간결한 양 당사자 보안 계산 등 다양한 맥락에서 SNARK의 유용성을 보여줍니다. 이 연구는 또한 SNARK의 존재가 ECRH의 필요성을 암시하며, 이러한 암호화 기본 요소 간의 기초적인 연결 고리를 확립한다는 것을 보여줍니다(Bitansky et al., 2011).
zkSNARK 시스템은 설정, 증명자, 검증자의 세 부분으로 구성됩니다. 설정 프로세스는 사전 정의된 보안 파라미터 l과 F-산술 회로 C를 사용하여 증명 키(PK)와 검증 키(VK)를 생성합니다. 회로의 모든 입력과 출력은 F 영역의 요소입니다. PK는 검증 가능한 증명을 생성하는 데 사용되며, VK는 생성된 증명을 검증하는 데 사용됩니다. 생성된 PK를 기반으로 증명자는 입력 x ∈ Fn과 증인 W ∈ Fh를 사용하여 증명 p를 생성하며, 여기서 C(x, W) = 0l. 여기서 C(x, W) = = 0l은 회로 C의 출력이 0l이고 x와 W는 회로 C의 입력 파라미터임을 의미합니다. n, h, l은 각각 x, W의 크기와 C의 출력을 나타냅니다. 마지막으로 검증자는 VK, x, p를 사용하여 p를 검증하고 검증 결과에 따라 증명을 수락하거나 거부하기로 결정합니다(Bitansky et al., 2011).
또한, zkSNARK에는 몇 가지 추가 기능이 있습니다. 첫째, 검증 프로세스를 단시간에 완료할 수 있으며 증명 크기는 일반적으로 몇 바이트에 불과합니다. 둘째, 증명자와 검증자 간의 동기식 통신이 필요하지 않으며, 모든 검증자가 오프라인에서 증명을 검증할 수 있습니다. 마지막으로, 증명자 알고리즘은 다항식 시간 내에만 구현할 수 있습니다. 그 이후로 몇 가지 개선된 zkSNARK 모델이 등장하여 성능과 적용 범위를 더욱 최적화했습니다(Bitansky et al., 2011).
2. Ben-Sasson의 모델: Ben-Sasson 등은 2013년과 2014년에 폰 노이만 RISC 아키텍처 프로그램 실행을 위한 새로운 zkSNARK 모델을 제안했습니다. 그런 다음 제안된 일반 회로 생성기를 기반으로 시스템을 구축하여 프로그램 실행을 검증하는 데 적용하는 것을 시연했습니다. 이 시스템은 산술 회로의 만족도를 검증하는 암호 증명 시스템과 프로그램 실행을 산술 회로로 변환하는 회로 생성기의 두 가지 구성 요소로 이루어져 있습니다. 이 설계는 기능성과 효율성, 특히 회로 생성기의 일반성과 출력 회로 크기의 부가적 의존성 측면에서 이전 작업을 능가합니다. 실험 평가에 따르면 이 시스템은 최대 10,000개의 명령어로 구성된 프로그램을 처리하고 5ms의 검증 시간으로 높은 보안 수준에서 간결한 증명을 생성할 수 있는 것으로 나타났습니다. 이 시스템의 가치는 블록체인 및 프라이버시 보호 스마트 컨트랙트와 같은 실용적인 애플리케이션을 위한 효율적이고 일반적이며 안전한 zk-SNARK 솔루션을 제공하는 데 있습니다( Ben-Sasson 외., 2013, 2014).
3. 피노키오 모델: 비대화형 영지식 인수 생성의 완전한 제품군으로 Parno 등(2013)이 제안했습니다(Parno et al. 외., 2013). 여기에는 개발자가 계산을 회로로 변환하는 쉬운 방법을 제공하는 고수준 컴파일러가 포함되어 있습니다. 이러한 컴파일러는 고수준 언어로 작성된 코드를 허용하므로 기존 알고리즘과 새로운 알고리즘을 쉽게 변환할 수 있습니다. 그러나 적절한 크기의 회로를 생성하기 위해 코드 구조에 몇 가지 제한이 있을 수 있습니다.
피노키오의 또 다른 특징은 이차 산술 프로그램(QAP)이라는 방법을 사용한다는 점입니다. 계산 작업을 검증 작업으로 효율적으로 변환하는 산술 프로그램(QAP)은 임의의 산술 회로를 다항식 집합으로 인코딩할 수 있으며 이러한 다항식을 생성하는 데 선형적인 시간과 공간 복잡성만 필요합니다.피노키오가 생성하는 증명의 크기는 288바이트로, 계산 작업의 복잡성과 입출력 크기에 따라 변하지 않습니다. 입력/출력 크기. 따라서 데이터 전송 및 저장의 오버헤드가 크게 감소하며, 피노키오의 검증 시간은 일반적으로 10밀리초로 이전 작업에 비해 5~7배 정도 단축됩니다. 일부 애플리케이션의 경우, 피노키오는 로컬 실행보다 더 빠른 검증 속도를 달성할 수도 있습니다. 작업자의 증명 오버헤드 감소: 피노키오는 또한 작업자의 증명 생성 오버헤드를 이전 작업에 비해 19~60배까지 줄여줍니다(Parno et al. 외., 2013).
4. 방탄 모델링: 2017 Benedikt Bünz 등(2018)은 새로운 비대화형 ZKP 모델을 설계했습니다. 신뢰할 수 있는 설정이 필요하지 않으며 증명 크기는 목격된 값의 크기에 따라 대수적으로 증가하며, 최소한의 그룹과 필드 요소를 사용하여 값이 특정 범위 내에 있음을 증명할 수 있어 기밀 거래의 구간 증명에 특히 적합합니다. 또한 방탄은 구간 증명의 집계를 지원하여 통신 및 검증 시간을 획기적으로 단축하는 간결한 다자간 계산 프로토콜을 통해 단일 증명을 생성할 수 있으며, 방탄은 암호화폐와 같은 분산되고 신뢰할 수 없는 환경에서 효율적이고 유용하도록 설계되었으며, 방탄은 전통적인 회로 기반 프로토콜이 아닙니다. 기존의 회로 기반 프로토콜이 아니기 때문에 SNARK보다 간결하지 못하며, Bulletproof를 검증하는 데 SNARK 증명을 검증하는 것보다 시간이 더 오래 걸립니다. 하지만 신뢰할 수 있는 설정이 필요하지 않은 시나리오에서는 더 효율적입니다.
5. Ligero 모델: Ames 등(2017)이 제안한 경량 영지식 증명 모델로, Ligero의 통신 복잡도는 검증된 회로 크기의 제곱근에 비례합니다. 또한 Ligero는 모든 충돌 방지 해시 함수에 의존할 수 있습니다. 또한, Ligero는 확률적 예측 모델에서 zkSNARK 체계가 될 수 있습니다. 이 모델은 신뢰할 수 있는 설정이나 공개 키 암호 시스템이 필요하지 않으며, Ligero는 매우 큰 인증 회로에 사용할 수 있습니다. 또한 애플리케이션의 중간 규모 회로에도 적합합니다.
Ishai와 Paskin(2007)은 부가적 동형 공개 키 암호화의 사용을 제안하여 대화형 PCP의 통신 복잡성을 줄이기 위해 통신 복잡성을 줄이기 위해 추가 동형 공개 키 암호화를 제안했습니다. 이후 Groth 등은 2006년부터 2008년 사이에 발표된 여러 연구에서 완벽한 완전성, 계산 정확성 및 완벽한 영지식 달성을 위해 이산 로그 문제와 이선 쌍을 기반으로 하는 NIZK 체계를 제안했습니다. 이 체계는 진술을 대수적 제약 조건 만족 문제로 표현하고, 페데르센의 헌신과 유사한 암호화 헌신 체계를 사용해 피아트-샤미르 휴리스틱 없이도 비선형 증명 길이와 비대화성을 달성합니다. 더 큰 CRS와 '지수적 지식'이라는 강력한 암호학적 가정이 필요하지만, 충분히 긴 CRS를 사용하면 일정한 증명 길이를 달성할 수 있습니다. 검증 및 증명에는 비용이 많이 들기 때문에 '시뮬레이션된 추출 가능성' 보안 모델을 사용하는 것이 좋습니다. 2006, 2008; Groth & Sahai, 2007).
6. Groth16 모델: 2016년에 Jens Groth가 제안한 효율적인 비대화형 영지식 증명 시스템입니다. 이 프로토콜은 타원 곡선 쌍과 이차 산술 절차(QAP)를 기반으로 하며 간결하고 빠르며 안전한 영지식 증명을 제공하는 것을 목표로 합니다.
7. 소닉 모델: 다항식 약속 체계, 페어링 및 산술 회로를 사용하여 Groth에 기반한 업데이트 가능한 CRS 모델로, M. Maller 외(2019)가 제안했습니다. 신뢰할 수 있는 설정이 필요하며, 이는 안전한 다자간 계산을 통해 달성할 수 있습니다. CRS가 생성되면 임의의 크기의 회로가 지원됩니다.
8. PLONK 모델: 2019년에 제안된 일반화된 zk-SNARK로, 쌍 다항식을 사용해 산술 회로 표현을 단순화하여 증명을 더 간단하고 효율적으로 만들며 다목적이며 재귀적 증명 조합을 지원합니다(Gabizon, 윌리엄슨과 시오보타루, 2019), Sonic의 증명 길이를 줄이고 증명 효율성을 개선한다고 주장하는 PLONK 모델은 아직 동료 검토를 거치지 않았습니다.
9. 말린 모델: 대수 증명 시스템의 효율성과 Sonic 및 PLONK의 일반적이고 업데이트 가능한 설정 속성을 결합하여 증명 크기와 검증 시간을 개선한 개선된 zk-SNARK 프로토콜 (Chiesa et 외., 2019).
10. SLONK 모델: 잭과 아리엘이 논문에서 소개한 새로운 프로토콜로, 특정 계산 효율성 문제를 해결하고 원래 PLONK 시스템의 기능을 향상시키기 위해 설계된 PLONK의 확장으로, 종종 기본 암호화 가정이나 구현을 변경하는 것을 포함합니다. (이더리움 리서치, 2019).
11. 슈퍼소닉 모델: 소닉을 신뢰할 수 있는 설정이 필요 없는 영지식 체계로 변환하는 새로운 다항식 약속 체계를 적용합니다. 양자 안전하지 않음(Bünz, Fisch & Szepieniec, 2019).
"일반인을 위한 증명"( 일반인을 위한 증명)은 2008년 골드바서, 칼라이, 로스블룸이 제안한 새로운 영지식 증명 방법입니다. 이 방법은 다양한 문제에 대해 원래의 상호 작용 증명 모델에서 다항식 시간 증명자를 위한 상호 작용 증명을 구축합니다. 이러한 증명은 Kalai 등의 변환을 통해 비대화형 영지식 증명으로 전환할 수 있습니다(Kalai, Raz &. 로스블룸, 2014).
12. 하이락스 모델: 일반인 증명에 기반하여, 와비 외(2018)는 증명자와 검증자 모두에게 비용이 적게 드는 저통신, 저비용 영지식 논증 체계인 하이락스를 처음 설계했습니다. 이 체계에서는 이 인수에 신뢰할 수 있는 설정이 없습니다. 배치문에 적용하면 검증 시간은 좋은 상수를 가진 산술 회로의 크기와 비선형적으로 관련됩니다. 증명자의 런타임은 좋은 상수를 가진 산술 회로 크기와 선형적으로 관련됩니다. 이산 로그 문제에 기반한 피아트-샤미르 휴리스틱을 사용하여 비대화성을 달성하며, 반양자 보안은 달성되지 않습니다.
13. 리브라 모델: 선형 증명 시간, 간결한 증명 크기 및 검증 시간을 갖춘 최초의 ZKP 모델입니다. 리브라에서는 검증 오버헤드를 줄이기 위해 증명자의 응답에 약간의 임의 다항식을 마스킹할 수 있는 방법으로 영지식 메커니즘이 구현됩니다. 또한 리브라는 회로의 입력 크기에만 의존하는 일회성 신뢰 설정이 필요하며, 리브라는 뛰어난 점근 성능과 증명자의 효율성이 뛰어납니다. 증명 크기와 검증 시간 성능도 매우 효율적입니다(Xie et al. 외., 2019).
증명자 알고리즘의 계산 복잡성 측면에서 Libra는 Ben-Sasson의 모델, Ligero, Hyrax, Aurora보다 성능이 뛰어나며, 또한 Libra의 증명자 알고리즘의 계산 복잡성은 회로 유형과 무관합니다(Partala, 응우옌 & amp; 피르티칸가스, 2020).
14. 스파르탄 모델: 스리나스 Setty(2019)가 제안한 영지식 증명 시스템으로, 신뢰할 수 있는 설정 없이 효율적인 증명을 제공하는 것을 목표로 하며 피아트-샤미르 변환을 사용하여 비대화성을 달성합니다. 경량 설계와 대규모 회로를 효율적으로 처리하는 능력으로 유명합니다.
Kilian(1992)은 다대수 대수를 구현하는 NP를 위한 최초의 대화형 영지식 논증 체계를 구축했습니다. 통신을 구현합니다. 이 체계는 충돌 방지 해시 함수, 대화형 증명 시스템(IP), 확률적으로 확인 가능한 증명(PCP)을 사용합니다. 증명자와 검증자(무작위 알고리즘)는 여러 라운드에 걸쳐 통신하며, 검증자는 증명자의 진술에 대한 지식을 테스트합니다. 일반적으로 일방적인 오류만 고려됩니다. 증명자는 항상 참 진술을 방어할 수 있지만 검증자는 낮은 확률로 거짓 진술을 받아들일 수 있습니다.2000년에 미칼리는 피아트-샤미르 변환을 사용하여 이 체계를 단일 메시지 비대화형 체계로 변환했습니다. 다음 구현은 이 접근 방식을 채택한 것으로 간주할 수 있습니다.
15. STARK 모델: 2018, ZK-STARKs (확장 가능한 투명한 지식 논증) 기법은 복잡한 증명을 처리할 때 zk-SNARK의 비효율성 문제를 해결하기 위해 2018년에 Ben-Sasson 등이 제안했습니다. 또한 개인 데이터에 대한 계산 무결성 검증 문제를 해결하고, 신뢰할 수 있는 당사자에 의존하지 않고도 투명하고 양자 이후에도 안전한 증명을 제공할 수 있습니다.
같은 해에 Ben-Sasson과 다른 사람들은 StarkWare 산업을 설립하고 이더리움의 공식 문서에 따르면 피아트-샤미르 패러다임을 통해 확률적 예측자 모델에서 비대화성을 가능하게 하는 ZK-STARKs 기반 최초의 확장성 솔루션인 StarkEx를 개발했습니다. 이 구조는 양자 안전하지만 보안은 리드-솔로몬 코드에 대한 비표준 암호화 가정에 의존합니다.ZK-STARKs는 ZK-SNARKs와 동일한 속성을 가지고 있지만 다음과 같은 장점이 있습니다: a)확장성: 더 빠른 인증 프로세스가 더 빨라집니다. 투명성: 인증 프로세스가 공개됩니다. 더 큰 증명 크기: 더 높은 거래 수수료가 필요함(StarkWare Industries, 2018, 2018)
16. 오로라 모델: Ben-Sasson 외(2019)가 제안한 STARK에 기반한 간결한 비대화형 인수( SNARG). 비인터랙션은 피아트-샤미르 구조를 기반으로 합니다. 이는 산술 회로의 만족도에 적용되며, Aurora의 인자 크기는 다대수적으로 회로 크기와 관련이 있습니다. 또한 오로라에는 몇 가지 매력적인 기능이 있습니다. 오로라에는 투명한 설정이 있습니다. 또한, 빠른 대칭 암호화가 블랙박스로 사용되며, 오로라는 증명 크기를 최적화합니다. 예를 들어 보안 매개변수가 128비트인 경우, Aurora의 증명 크기는 최대 250KB입니다. 증명 크기와 계산 오버헤드를 최적화함으로써 Aurora와 Ligero는 리소스가 제한된 장치에서 영지식 증명을 수행하는 데 매우 적합합니다. 이러한 최적화는 효율성을 향상시킬 뿐만 아니라 영지식 증명 기술의 범위를 넓혀 보다 실용적인 시나리오에서 사용할 수 있도록 합니다.
17. 간결한 오로라 모델: 같은 논문에서 Ben-Sasson 외(2019)가 제안한 것으로, 보다 최적화된 증명 크기와 검증 프로세스를 제공하는 오로라 프로토콜의 확장입니다. Aurora의 투명한 설정과 보안 기능을 유지하면서 효율성을 높였습니다.
18. 프랙탈 모델: 재귀적 조합을 사용해 효율성과 확장성을 개선하는 전처리 SNARK로, Chiesa 등(2020)이 제안했습니다. 이 모델은 로그 증명 크기와 검증 시간을 활용하며 특히 복잡한 계산에 적합합니다.
2세대(G2)- 모든 회로에 대해 처음에 한 번 설정됩니다. PlonK, Sonic, Marlin, slonk 및 Libra
3세대(G3)는 신뢰할 수 있는 설정이 필요하지 않은 - 증명 시스템입니다. 불릿프루프, 스타크, 스파르탄, 프랙탈, Fractal, Fractal span>, Supersonic, Ligero, Aurora 및 Succinct 오로라 (챠프코, 부크미로비치, 네디치, 2019; 파탈라. 응우옌 & 피르티칸가스, 2020).
앞부분은 영지식 증명에 대한 ZKP에 대한 소개였습니다. >의 영지식 증명에 대해 설명한 다음, 컴퓨팅에서의 발전을 간략하게 설명하겠습니다.
2019년에 안드레프(Andreev)> 등이 "에 논문을 발표했습니다. ZkVM. 빠르고, 비공개적이며, 유연한 블록체인 계약" 컨퍼런스에서 영지식 증명 시스템의 구현으로 ZK-VM 개념이 처음 소개되었습니다. ZK-VM 의 목표는 입력 데이터를 공개하지 않고 프로그램 실행의 정확성을 검증하는 가상 머신 프로그램을 실행하여 영지식 증명을 생성하는 것입니다.
VM, (Virtual 머신, (가상 머신, 가상 머신)은 물리적 컴퓨터와 유사하게 프로그램을 실행할 수 있는 컴퓨터 시스템을 소프트웨어로 에뮬레이션한 것입니다. VM은 소프트웨어 테스트 및 개발 등을 위해 독립형 운영 체제 환경을 만드는 데 자주 사용됩니다. VM 또는 VM 추상화는 대부분의 경우 컴퓨터의 처리 장치(CPU 추상화와 동일하게 이해할 수 있으며, 이는 컴퓨터의 처리 장치를 추상화하는 것을 의미합니다.) US">CPU
)의 복잡한 연산과 아키텍처를 컴퓨터 프로그램의 설계와 실행을 간소화하는 데 사용되는 일련의 간단하고 상호 운용 가능한 명령어 집합 아키텍처(ISA)로 추상화하는 것을 말합니다. 이 추상화에서 컴퓨터 프로그램은 실제 CPU의 작동 동작을 모방하는 가상 머신(VM)을 통해 실행될 수 있습니다(Henderson, 2007).영지식 증명(ZKP)은 일반적으로 CPU 추상화를 통해 수행해야 합니다. 이 설정은 증명자가 비공개 입력에 대해 공개 프로그램을 실행하고 프로그램이 올바르게 실행되고 계산의 입력이나 중간 상태를 공개하지 않고 주장된 출력을 생성한다는 것을 검증자에게 증명하고자 하는 것입니다. 이 경우 CPU 추상화는 프로그램이 제어된 가상 환경에서 실행되는 동시에 증명을 생성할 수 있기 때문에 유용합니다(Arun, Setty & Thaler, 2024).
예: 증명자가 해시된 비밀번호를 공개하지 않고 이를 증명하고자 하는 경우:
비밀번호 → 해시 함수 → 해시
비공개 → 공개
일반적으로, 증명자는 다음을 수행할 수 있어야 합니다. 해시 연산을 수행하는 코드를 실행하고 누구나 증명의 정확성, 즉 증명자가 실제로 주어진 해시 값의 유효한 사전 이미지를 가지고 있는지 확인할 수 있는 "증명을 생성합니다.
이러한 추상 증명을 생성하는 시스템을 흔히 "zkVM"이라고 부릅니다. 이 이름은 사실 오해의 소지가 있습니다. ZKVM이 반드시 제로 지식을 제공하는 것은 아니기 때문입니다. 간단히 말해, ZKVM은 영지식 증명에 초점을 맞춘 가상 머신으로, 기존 VM의 기능을 확장하여 일반적으로 영지식 회로 개발의 장벽을 낮추고 모든 애플리케이션 또는 계산에 대한 증명을 즉시 생성하는 ( Zhang et al. 외., 2023).
1. 메인스트림 ZKVM
이 ZKVM은 광범위한 애플리케이션과 개발 환경을 위해 기존의 표준 ISA(명령어 집합 아키텍처) 및 컴파일러 툴체인을 활용합니다.
- RISC Zero(2021): 풍부한 컴파일러 에코시스템과 함께 RISC-V 명령어 집합을 사용합니다(Bögli, 2024).
- Polygon Miden(2021): 쉽고 효율적인 개발을 위한 표준 기반 ISA(Chawla, 2021). 2021).
- zkWASM(2022): 널리 채택된 표준 명령어 집합인 웹어셈블리(WASM) 명령어 집합에 대한 영지식 증명을 구현하는 zkWASM(Delphinus Lab, 2022 ).
2. EVM과 호환되는 ZKVM
이러한 ZKVM은 이더넷 가상 머신(EVM)과 호환되도록 특별히 설계되었으며 이더넷 바이트코드를 직접 실행할 수 있습니다.
- zkEVM 프로젝트: zkSync(Matter. Labs , 2020) 및 Polygon과 같은 여러 프로젝트가 EVM과의 바이트코드 수준 호환성을 위해 노력하고 있습니다. Labs , 2020) 및 Polygon Hermez(Polygon Labs . 2021).
3. 영지식 최적화(영지식 친화적) ZKVM
이 ZKVM은 영지식 증명의 효율성과 성능을 최적화하고 특정 애플리케이션 시나리오를 위해 설계되었습니다.
-Cairo-VM(2018): 간단하고 SNARK 증명과 호환되며, 명령어 세트가 산술 친화적으로 설계되어 영지식 회로에서 덧셈, 곱셈 등과 같은 기본 산술 연산을 쉽게 구현할 수 있도록 합니다(StarkWare, 2018).
- Valida(2023): 알고리즘을 최적화하여 증명 생성에 필요한 연산 자원과 시간을 줄이는 등 특정 애플리케이션에 최적화되어 있으며, 경량 설계로 다양한 하드웨어 및 소프트웨어 환경에 적합합니다(Lita 재단, 2023).
- TinyRAM(2013): 표준 툴체인에 의존하지 않음: 단순화되고 최적화된 설계로 인해 일반적으로 LLVM 또는 GCC 툴체인을 지원하지 않으며 소규모 맞춤형 소프트웨어 구성 요소에만 사용할 수 있습니다( Ben-Sasson et al., 2013 ).
일반적인 견해는 VM이 단순할수록 단계당 게이트 수가 적은 회로로 변환된다는 것입니다. 이는 특히 단순하고 SNARK 친화적인 VM(예: TinyRAM 및 Cairo-VM)의 설계에서 가장 잘 드러납니다. 그러나 실제 CPU의 기본 연산을 단순한 VM에서 구현하려면 많은 기본 명령어가 필요하기 때문에 추가적인 오버헤드가 필요합니다(Arun, Setty & Thaler, 2024).
일반적으로 회로는 계산 절차의 각 단계를 단계별로 "실행
"합니다(신뢰할 수 없는 계산기의 도움으로). 계산 절차의 각 단계(신뢰할 수 없는 "제안 입력 "의 도움으로). CPU를 실행하는 단계는 개념적으로 두 가지 작업을 포함합니다: (1) 해당 단계에서 실행해야 하는 기본 명령어를 식별하고 (2) 명령을 실행하고 적절하게 업데이트하는 CPU 상태를 업데이트합니다. 기존 프론트엔드는 신중하게 설계된 게이트 또는 제약 조건을 통해 이러한 작업을 수행합니다. 이는 시간이 많이 걸리고 오류가 발생하기 쉬우며 실제 필요한 것보다 훨씬 더 큰 회로를 만들게 됩니다(Arun, Setty & Thaler, 2024; Zhang et al., 2023).장점:
1. 기존 ISA 활용: 예. 기존 컴파일러 인프라와 툴체인을 활용할 수 있으므로 인프라를 처음부터 구축할 필요가 없습니다. 기존 컴파일러를 직접 호출하여 고급 언어로 작성된 증인 검사기를 ISA용 어셈블리 코드로 변환할 수 있으며, 이전 감사 또는 기타 검증 작업의 이점을 활용할 수 있습니다.
2. 여러 프로그램에 대한 단일 회로 지원: 다른 접근 방식은 각 프로그램에 대해 프런트엔드를 다시 실행해야 하는 반면, zkVM은 특정 시간 제한에 도달할 때까지 단일 회로로 모든 프로그램을 실행할 수 있습니다.
3. 반복적으로 구조화된 회로: 프런트 엔드는 반복적인 구조의 회로를 출력하여 백엔드가 더 빠르게 처리할 수 있도록 합니다(Arun, Setty & Thaler, 2024; Zhang et al.
단점:
1. 일반성으로 인한 오버헤드: 가능한 모든 CPU 명령어 시퀀스를 지원하기 위해 zkVM 회로는 일반성에 대한 비용을 지불해야 하므로 회로의 크기와 증명 비용이 증가하게 됩니다.
2. 고비용 연산: 암호화 연산과 같은 일부 중요한 연산을 zkVM에서 구현하는 데는 매우 많은 비용이 듭니다. 예를 들어, ECDSA 서명 검증은 실제 CPU에서 100마이크로초가 걸리고 RISC-V 명령어에서는 수백만 개의 명령어가 필요합니다. 따라서 zkVM 프로젝트에는 특정 기능을 계산하기 위해 수작업으로 최적화된 회로와 룩업 테이블이 포함되어 있습니다.
3. 높은 증명 비용: 매우 간단한 ISA의 경우에도 기존 zkVM은 증명자에게 여전히 매우 비쌉니다. 예를 들어, Cairo-VM의 증명자는 단계당 51개의 도메인 요소를 암호화하여 제출해야 하는데, 이는 원시 명령어를 실행하려면 실제 CPU에서 수백만 개의 명령어가 필요할 수 있으므로 복잡한 애플리케이션에 적용하는 데 제한이 있다는 것을 의미합니다(Arun, Setty & Thaler, 2024; Zhang et al.
ZKEVM(영지식 이더 가상 머신) 및 ZKVM(영지식 가상 머신)은 모두 영지식 증명(ZKP)의 애플리케이션입니다. 기술을 가상 머신에 적용한 것입니다. 이더 가상 머신(EVM)은 스마트 콘트랙트의 배포와 실행을 처리하는 이더 블록체인 시스템의 일부로, 스택 기반 아키텍처를 가지고 있으며 특정 명령어 세트(예: 로깅 작업, 실행, 메모리 및 스토리지 액세스, 제어 흐름, 로깅, 호출 등)를 위한 연산 및 스토리지를 제공하는 컴퓨팅 엔진이며, EVM의 역할은 스마트 계약의 작업을 적용한 후 이더의 상태를 업데이트하는 것입니다. ZKEVM은 이더리움용으로 설계되었으며 주로 트랜잭션 프라이버시를 보호하면서 스마트 컨트랙트 실행의 정확성을 검증하는 데 사용되며, 각 명령어는 상태 증명과 실행 정확성 증명(Čapko)을 포함한 증명을 제공해야 하는 ZK 시스템에서 실행되도록 EVM 명령 집합을 변환합니다, 부크미로비치와 네디치, 2019).
ZKEVM의 주류 솔루션은 STARKWARE, ZkSync, Polygen-Hermez, Scroll 등이며, 다음은 이러한 프로젝트 중 몇 가지를 간략히 소개합니다(Čapko, Vukmirović & Nedić, 2019):
스타크웨어: 벤 사손 외(2018)에 의해 설립되었으며, 스타크 영지식 증명 기술을 사용하여 블록체인의 프라이버시와 확장성을 개선하는 데 전념하고 있습니다
zkSync : Alex. Gluchowski(2020)와 다른 사람들이 zk-롤업에 기반한 이더리움 레이어 2 확장 솔루션을 제안하는 Matter Labs를 설립했습니다.
Polygon-Hermez: 원래 2020년에 출시된 독립형 프로젝트였던 Hermez는 2021년 8월 Polygon에 인수되어 Polygon-Hermez가 되었습니다. Hermez는 처리량이 높은 zk-롤업 솔루션에 중점을 두고 있습니다.
스크롤: 장과 펭이 설립한 스크롤은 거래 처리량을 늘리고 가스비를 낮춰 전반적인 이더 성능과 사용자 경험을 개선합니다.
일반적으로 EVM과의 호환성 수준에 따라 다음과 같이 분류할 수 있습니다(Čapko. 2019):
1. EVM-EVM 호환 스마트 컨트랙트 기능 수준 호환성, 예: 스타크웨어, zkSync
2. EVM-동등성, EVM-명령 수준 호환성(동급), 예: polygen-Hrmez, 스크롤
영지식 기반 이더리움
영지식 기반 이더리움 시스템 개선 솔루션은 그림 1을 참조하세요
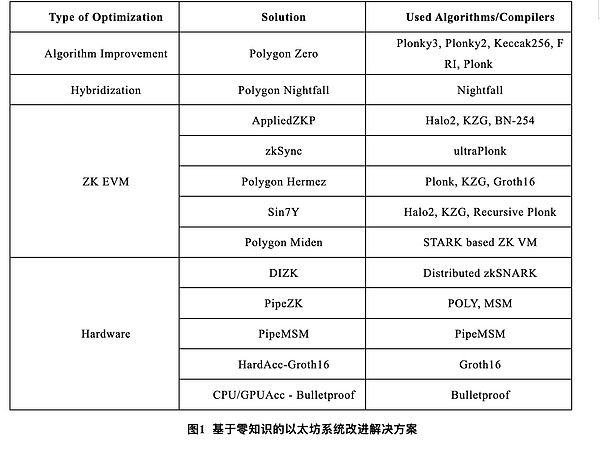
2. ZKEVM 작동 원리
노드 프로그램 처리: 노드 프로그램은 실행 로그, 블록 헤더, 트랜잭션, 컨트랙트 바이트코드, 머클 증명 등을 처리 및 검증하고 이 데이터를 zkEVM으로 전송하여 처리합니다. /span>로 전송하여 처리합니다.
ZK 증명 생성: zkEVM은 회로를 사용하여 의 실행 결과를 생성합니다.
하비에르 밀레이 대통령의 정책으로 인해 라 리오하와 같은 지방에서 자체 화폐 발행을 고려하고 있는 아르헨티나의 경제 상황을 살펴보세요. 이러한 지방 정부의 이니셔티브가 갖는 의미, 로사리오에서 디지털 통화의 혁신적인 사용, 아르헨티나 경제와 글로벌 금융 트렌드에 미치는 광범위한 영향에 대해 자세히 알아보세요.
 Brian
Brian바이낸스 사건에서 디지털 자산의 분류를 면밀히 검토한 에이미 버먼 잭슨 연방 판사의 중요한 법정 검토를 살펴보세요. 이 글에서는 법적 미묘한 차이, 주요 논거, 암호화폐 규제의 미래에 미칠 잠재적 영향에 대해 살펴봅니다.
 Weiliang
Weiliang디지털 세계에서 'AI의 옷 벗기기'가 놀라울 정도로 증가하고 있는 상황을 살펴보세요. AI 도구가 합성 음란 콘텐츠를 생성하여 개인 정보 보호와 무결성에 위협을 가하는 윤리적, 법적 영향을 알아보세요. 이 긴급한 문제를 해결하기 위한 글로벌 대응 방안에 대해 알아보세요.
 Miyuki
Miyuki최근 이더리움의 대체 불가능한 토큰 프로젝트인 Milady Maker가 100만 달러의 수수료 유용과 소셜 미디어 하이재킹을 통해 익스플로잇을 당한 사건을 살펴보세요. 샬롯 팡의 대응과 이러한 디지털 장애를 극복하기 위한 커뮤니티의 결의를 알아보세요.
 Brian
Brian까다로운 디도스 공격을 받은 만타 토큰 출시 당시 만타 네트워크의 회복탄력성에 대해 알아보세요.
 Weiliang
Weiliang바나나건 스나이핑 도구를 사용하여 사토시VM 토큰 출시 후 3시간 만에 677만 달러의 수익을 올린 암호화폐 트레이더의 놀라운 이야기를 알아보세요.
 Miyuki
MiyukiETF와 온체인 지표의 영향부터 탈중앙화 거래소의 변화와 정치적 영향력까지, 디지털 금융의 발전을 이끄는 요인에 대해 자세히 알아보세요.
 Brian
Brian디도스 공격으로부터의 신속한 복구와 11월 해킹을 비롯한 사이버 도전과제를 극복한 HTX의 탄력적인 여정을 살펴보세요.
 Weiliang
Weiliang미국 ETF 시장에서 은을 능가하고 금에 도전하는 비트코인 ETF의 혁신적인 여정을 살펴보세요.
 Miyuki
Miyuki비트코인 가격, GBTC의 전략적 전환, 경쟁 환경이 어떻게 투자자 전략과 암호화폐 투자의 미래를 재편하고 있는지 알아보세요.
 Brian
Brian