저자: 비탈릭 부테린, 번역: 커트 팬, XPTY
이 글은 SNARK와 STARK의 기본 작동 방식에 익숙하다고 가정하고 작성되었으므로 익숙하지 않은 경우 이 글의 이전 섹션을 읽어보시길 권장합니다. 피드백과 토론을 제공해 주신 Eli 벤 사손, 샤하르 파피니, 아비후 레비, 그리고 starkware의 다른 분들께 특별히 감사드립니다.

https://en.wikipedia.org/wiki/Karatsuba_algorithm
https://polygon.technology/blog/plonky2-a-deep-dive
https://blog. icme.io/small-fields-for-zero-knowledge/
이 같은 변화로 인해 이미 증명 속도가 극적으로 증가했으며, 특히 Starkware는 M3 노트북에서 초당 62만 개의 포세이돈2 해시를 증명할 수 있게 되었습니다. 특히 이는 해시 함수의 일부로 포세이돈2를 신뢰하기만 한다면 효율적인 ZK-EVM 구축에서 가장 어려운 부분 중 하나가 효율적으로 해결되었다는 것을 의미합니다. 하지만 이러한 기술은 어떻게 작동하며, 이러한 도메인에서 암호화 증명(보안을 위해 종종 큰 정수가 필요한)은 어떻게 구성될까요? 그리고 이러한 프로토콜은 비니우스와 같은 보다 이색적인 구조와 어떻게 비교될까요? 이 글에서는 이러한 뉘앙스 중 일부를 살펴보고, 특히 효율적인 메르센31 도메인과 호환되도록 설계된 몇 가지 고유한 특성을 가진 Circle STARKs(Starkware의 stwo, Polygon의 plonky3 및 제가 직접 파이썬으로 구현)라는 구조에 중점을 두고 설명합니다.
https://x.com/StarkWareLtd/status/1807776563188162562
https://vitalik.eth.limo/general/2022/08/04/zkevm.html
https:// vitalik.eth.limo/general/2024/04/29/binius.html
https://www.irreducible.com/posts/binius- hardware-optimised-snark
https://eprint.iacr.org/2024/278
https://eprint.iacr.org/2024/278
https://github.com/starkware-libs/stwo
https://github.com/Plonky3/Plonky3
https://github.com/ethereum/research/tree/master/circlestark
작은 도메인의 일반적인 문제
해시 기반 수행 시 발생하는 문제 해시 기반 증명(또는 실제로 모든 유형의 증명)을 할 때 가장 중요한 '요령' 중 하나는 임의의 지점에서 다항식에 대한 것을 증명하는 대신 기본 다항식에 대한 것을 증명하는 것입니다.

- https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic

이 문제에 대한 두 가지 자연스러운 해결책이 있습니다:

- https://www2.clarku.edu/faculty/djoyce/ complex/mult.html

여기 구현은 최적이 아닙니다(최적화를 위해 다음과 같이 최적화할 수 있습니다. 카라츠바를 사용하여 최적화할 수 있음), 원리를 보여줄 뿐

정기 금요일


- https://eccc.weizmann.ac.il/report/2017/134/

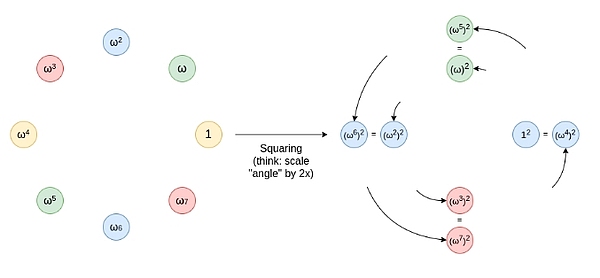

Circle FRI

- https://elibensasson.blog/why-im-excited-by- circle-stark-and-stwo/
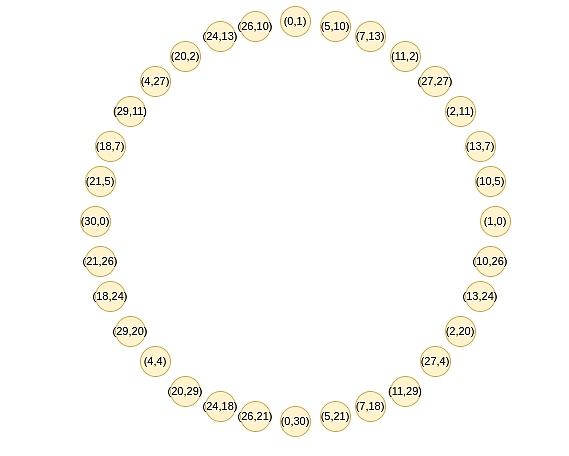
이 점들은 최근 삼각법이나 복소수 곱셈을 공부했다면 익숙한 덧셈의 법칙을 따릅니다:
- https:// unacademy.com/content/cbse-class-11/study-material/mathematics/algebra-of-complex-numbers-multiplication/

<>< p style="text-align: 가운데;">
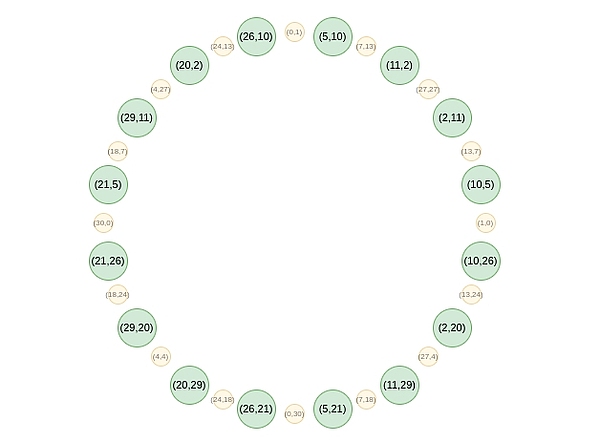
< p style="text-align: center;">


2라운드부터 매핑이 변경됩니다.

< h2>서클 FFT

- https:/. /vitalik.eth.limo/general/2019/05/12/fft.html


- https://www. researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_. Finite_Fields
이제부터는 일반 STARK와 비교하여 CIRCLE STARK를 구현할 때 달라지는 좀 더 난해한 세부 사항에 대해 알아보겠습니다.
수분

- https://eprint. iacr.org/2019/336


소멸하는 다항식

비트 순서 반전

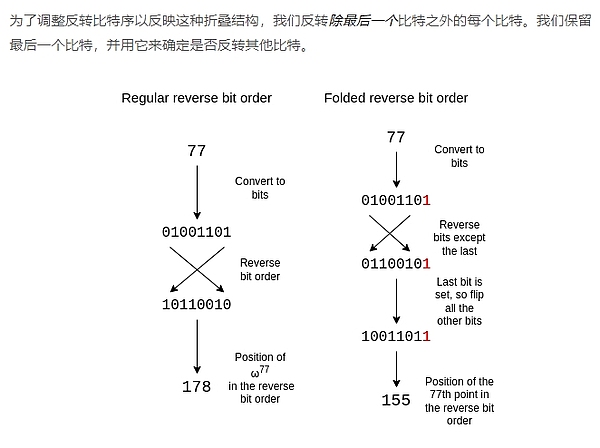

효율성

그래서, 동그라미 Binius는 크기가 다른 필드를 혼합 및 매칭하여 모든 항목에 대해 보다 효율적인 비트 패킹을 제공할 수 있으므로 훨씬 더 강력합니다. 또한 Binius는 룩업 테이블의 오버헤드 없이 32비트 덧셈을 수행할 수 있는 옵션도 제공합니다. 그러나 이러한 이점은 (제 생각에는) 이론적 복잡성이 상당히 높아지는 대가를 치르게 되며, 서클 STARK(및 BabyBear 기반의 일반 STARK)는 개념적으로 매우 간단합니다.
결론: 서클 스탁에 대해 어떻게 생각하시나요?
서클 스탁은 일반 스탁에 비해 개발자에게 추가적인 복잡성을 유발하지 않습니다. 구현 측면에서 보면 기본적으로 이 세 가지 문제가 서클 FRI와 일반 FRI의 유일한 <차이점>입니다. 서클 FRI가 작동하는 '다항식'의 수학은 직관적이지 않고 이해하고 이해하는 데 시간이 걸립니다. Circle의 복잡한 수학은 체계적이지 않고 캡슐화되어 있지만, 개발자가 너무 많이 보지 않도록 숨겨져 있습니다.
https://vitalik.eth.limo/general/2022/02/28/complexity.html
https://vitalik.eth.limo/general/2022/02/28/complexity.html
원 FRI와 원 FFT를 이해하는 것은 다른 "이색적인" FFT, 특히 이전에 Binius와 LibSTARK에서 사용되었던 이진 도메인 FFT를 이해하는 데도 좋은 지적 방법이 될 수 있습니다. 몇 대 1 매핑을 사용하고 타원 곡선 포인트 연산에 잘 작동하는 타원 곡선 FFT와 같은 좀 더 이색적인 구조도 LibSTARK에서 사용할 수 있습니다.
https://github.com/ethereum/research/blob/master/binius/binary_ ntt.py#L60
https://github.com/elibensasson/libSTARK
https://arxiv.org/abs/2107.08473
메르센31, 베이비베어, 그리고 비니우스 같은 바이너리 도메인 기술을 결합함으로써 STARK의 "베이스 레이어" 효율 한계에 접근하고 있다고 생각합니다. " 효율성의 한계에 다가가고 있다고 생각합니다. 현 시점에서는 해시 함수 및 서명과 같은 기본 요소의 가장 효율적인 산술화(그리고 이를 위해 기본 요소 자체를 최적화), 더 많은 병렬화를 위한 재귀적 구조, 개발자 경험을 향상시키기 위한 VM의 산술화 및 기타 상위 계층 작업으로 STARK 최적화의 영역이 옮겨갈 것으로 예상합니다.
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Catherine
Catherine Beincrypto
Beincrypto Coindesk
Coindesk Bitcoinist
Bitcoinist 链向资讯
链向资讯 Ftftx
Ftftx Cointelegraph
Cointelegraph