스타트업의 자금 조달 방식, SAFE
SAFT와 SAFE는 간단하고 유연하며 효율적으로 자금을 조달할 수 있는 방법이며, 몇 페이지에 불과하며, SAFT는 통화권 자금 조달에, SAFE는 주식 자금 조달에 사용됩니다.
 JinseFinance
JinseFinance
출처: 덴체인 커뮤니티
현업 프로그래머를 위한 ZKP 튜토리얼 소개입니다.
얼룩말에 줄무늬가 있는 이유를 아십니까? 한 가지 이론은 위장의 한 형태라는 것입니다. 얼룩말이 모여 있으면 사자가 먹이를 구별하기가 더 어려워집니다. 사자는 먹이를 사냥하기 위해 무리에서 먹이를 분리해야 합니다[^1].
인간도 무리를 지어 숨는 것을 좋아합니다. 이에 대한 구체적인 예는 여러 사람이 집단이라는 이름으로 한꺼번에 행동하는 경우입니다. 연방주의자 논문이 이런 방식으로 만들어졌습니다[^2]. 또 다른 예로는 1930년대 프랑스 수학자 그룹의 집단 필명인 부르바키가 있습니다. 이로 인해 엄밀성과 공리적 방법에 중점을 둔 현대 수학의 많은 부분이 완전히 다시 쓰이게 되었습니다[^3].
<그림 style="text-align: 가운데;">
디지털 시대에 그룹 채팅에서 논쟁의 여지가 있는 메시지를 보내고 싶다고 가정해 봅시다. 어떤 메시지인지 밝히지 않고 자신이 그 메시지의 일부임을 증명하고 싶을 것입니다. 이를 위해 디지털 영역에서 암호화를 어떻게 사용할 수 있을까요? 그룹 서명이라는 것을 사용할 수 있습니다.
전통적으로 그룹 서명은 수학적으로 매우 복잡하고 구현하기 어렵습니다. 하지만 영지식 증명(ZKP)을 사용하면 이 수학적 문제가 간단한 프로그래밍 작업으로 바뀝니다. 이 글이 끝나면 여러분은 자신만의 그룹 서명을 작성할 수 있을 것입니다.
이 글에서는 기본적인 영지식 증명(ZKP)을 처음부터 작성하는 방법을 보여드리겠습니다.
새로운 기술 스택을 배울 때는 편집-구축-실행 주기를 최대한 빨리 익히고 싶을 것입니다. 그래야만 우리 자신의 경험을 통해 학습을 시작할 수 있습니다.
우리는 먼저 환경을 설정하고, 소위 신뢰할 수 있는 설정을 수행하는 간단한 프로그램을 작성한 다음, 가능한 한 빨리 증명을 생성하고 검증하는 것부터 시작할 것입니다. 그런 다음 프로그램을 개선할 수 있는 몇 가지 방법을 파악하고 개선 사항을 구현한 후 테스트할 것입니다. 이 과정에서 실제로 ZKP를 프로그래밍하기 위한 더 나은 멘탈 모델을 구축할 것입니다. 마지막으로, 처음부터 ZKP를 작성하는 데 익숙해질 것입니다.
특정 메시지를 보냈음을 증명할 수 있는 간단한 서명 체계를 단계적으로 구축할 것입니다. 이 코드가 하는 일과 그 이유를 이해할 수 있을 것입니다.
# clone 리포지토리를 열고 준비 스크립트를 실행합니다
git clone git@github.com:oskarth/zkintro-tutorial.git
cd zkintro-tutorial
# 실행하기 전에 이 파일의 내용을 살펴보세요
less . /scripts/prepare.sh
. /scripts/prepare.sh
를 찾아보는 것이 좋습니다. /scripts/prepare.sh에서 설치되는 내용을 확인하거나 수동으로 설치하는 것이 좋습니다. 실행이 완료되면 설치 완료라는 메시지가 표시되고 오류가 없어야 합니다.
문제가 발생하면 여기에서 최신 공식 문서를 참조하세요 [7]. 완료되면 다음 버전(또는 그 이상)이 설치되어 있어야 합니다:
&& pragma circom 2.0.0;
template Multiplier2 () {
signal input a;
signal input b;
signal input c;
c <== a * b;
}
c c;
이것은 우리의 특별한 프로그램 또는 _circuit_입니다. [^6] 줄별 분석:
template multiplier() - 템플릿은 대부분의 프로그래밍 언어에서 객체에 해당하며 일반적인 추상화 형태입니다
신호 입력 a; - 첫 번째 입력, a; 입력은 기본적으로 비공개입니다
신호 입력 b; - 두 번째 입력, b; 다시 기본적으로 비공개
신호 출력 b; - 우리의 출력, c; 출력은 항상 공개
c <== a * b; - 이것은 두 가지 일을 합니다: 신호 c를 에 할당하고 c가 a와 . b product
component main = Multiplier2() - 메인 컴포넌트를 인스턴스화합니다
가장 중요한 줄은 c <== a * b;입니다. 여기서 실제로 제약 조건을 선언합니다. 이 표현식은 실제로 <--(할당)과 ===(방정식 제약 조건) 두 가지의 조합입니다. [^7] Circom의 제약 조건은 상수, 덧셈 또는 곱셈과 관련된 연산에만 사용할 수 있습니다. 이 제약 조건은 방정식의 양쪽이 같아야 한다는 것을 강제합니다. [^8]
제약 조건에 대하여제약 조건은 어떻게 작동하나요? 스도쿠와 같은 맥락에서 제약 조건은 "1과 9 사이의 숫자"라고 말할 수 있습니다. 그러나 Circom의 맥락에서 이것은 하나의 제약 조건이 아니라 더 간단한 방정식 제약 조건 집합을 사용하여 표현해야 합니다(====). [^9]
왜 그럴까요? 기본 수학과 관련이 있습니다. 기본적으로 대부분의 ZKP는 다항식에 대한 계산을 나타내는 _산술 회로_를 사용합니다. 다항식으로 작업할 때 상수를 쉽게 도입하고, 더하고, 곱하고, 같은지 확인할 수 있습니다. [^10] 다른 연산은 이러한 기본 연산의 관점에서 표현해야 합니다. ZKP를 작성하기 위해 이를 자세히 알 필요는 없지만, 내부에서 무슨 일이 일어나는지 알면 유용할 수 있습니다. [^11]
회로를 다음과 같이 시각화할 수 있습니다.
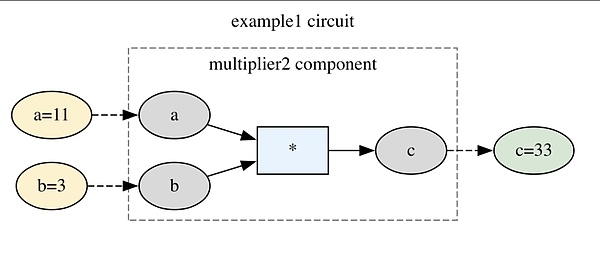
우리의 회로참고로, 최종 파일은 example1-solution.circom에서 찾을 수 있습니다. 구문에 대한 자세한 내용은 공식 문서 [9]을 참조하세요.
다음과 같이 실행하여 회로를 컴파일할 수 있습니다.
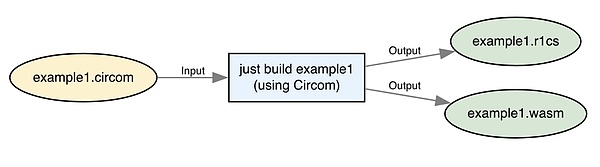
이것은 다음과 같습니다. circom을 호출하여 example1.r1cs 및 example1.wasm 파일을 생성하기 위한 간단한 래퍼입니다. 다음과 같은 내용이 표시되어야 합니다:
{< br> "pi_a": ["15932[...] 3948", "66284[...] 7222", "1"],
"17667"["17667 [...] 0525", "13094 [...] 1600"],
["12020 [...] 5738", "10182[...] "pi_c": ["18501(...) 3969", "13175[...] 3552", "1"],
"curve ": "bn128"
}
여러 수학 객체(세 개의 타원 곡선 요소) pi_a, pi_b, pi_c의 형태로 증명을 지정합니다. 코드> 형식으로 증명을 지정합니다. [20] 또한 프로토콜(groth16)과 사용된 _curve_(bn128, 지금은 수학적 구현 세부 사항은 무시하겠습니다)에 대한 메타데이터도 포함합니다. 이를 통해 검증자는 이 증명을 올바르게 검증하기 위해 어떻게 처리해야 하는지 알 수 있습니다.
증명이 얼마나 짧은지 주목하세요. 특정 프로그램이 아무리 복잡하더라도 그 크기는 이 정도에 불과합니다. 이는 _친숙한 영지식 증명 소개_[sup][10]에서 설명한 ZKP의 간결성 속성을 보여줍니다. 위의 명령은 또한 _public outputs_를 출력합니다.
이것은 증인과 회로에 해당하는 모든 공개 출력의 목록입니다. 이 경우, c: 33에 해당하는 공개 출력이 하나 있습니다.[^21]
우리는 무엇을 증명했나요? 우리는 두 개의 비밀 값인 <코드>a와 <코드>b의 곱이 33이라는 것을 알고 있습니다. 이것은 이전 게시물에서 설명한 <개인 정보 보호> 속성을 보여줍니다.
이 증명은 단독으로는 유용하지 않으며 함께 제공되는 공개 출력이 필요하다는 점에 유의하세요.
다음으로 증명을 검증해 보겠습니다. 실행:
just verify_proof example1

이를 위해서는 인증 키, 공개 출력 및 증명이 필요합니다. 이를 통해 증명을 확인할 수 있습니다. "Proof Validated"가 출력되어야 합니다. 검증자는 비공개 입력은 절대로 건드리지 않습니다.
출력을 변경하면 어떻게 되나요? example1/target/public.json를 열고 33을 34로 변경한 후 위의 명령을 다시 실행합니다.
더 이상 증명이 유효하지 않다는 것을 알 수 있습니다. 이는 증명에서 곱이 34인 두 개의 숫자가 있다는 것을 증명하지 못하기 때문입니다.
축하합니다, 이제 첫 번째 ZKP 프로그램을 작성하고 그럴듯한 설정을 수행하여 증명을 생성하고 마침내 검증을 완료했습니다!
ZKP의 두 가지 주요 속성은 무엇이며 그 의미는 무엇인가요?
증명자의 역할은 무엇이며 어떤 입력이 필요하나요? 검증자는 어떤 역할을 하나요?
c <== a * b; 줄이 무엇을 하는지 설명하세요.
신뢰 설정이 필요한 이유는 무엇인가요? 제품을 어떻게 사용하나요?
코드: 증명을 생성하고 확인할 때까지 example1를 작성하세요.
위 회로를 통해 두 (비밀) 숫자의 곱을 알고 있음을 증명했습니다. 이는 많은 암호학의 기초가 되는 소인수분해 문제와 밀접한 관련이 있습니다. [22] 매우 큰 수가 있을 경우, 그 소수의 곱이 큰 수와 같도록 두 소수를 찾는 것은 어렵다는 것입니다. 반대로 두 수의 곱이 다른 수와 같은지 확인하는 것은 매우 간단합니다. [하지만 우리 회로에는 큰 문제가 있습니다. 보이시나요?
입력을 "1"과 "33"으로 쉽게 변경할 수 있습니다. 즉, 숫자 <코드>c는 항상 1과 <코드>c의 곱이 됩니다. 그다지 인상적이지 않나요?
우리가 하고 싶은 것은 <코드>a 또는 <코드>b가 1과 같을 수 없도록 다른 _제약 조건_을 추가하는 것입니다. 이렇게 하면 적절한 정수 인수분해를 수행해야 합니다.
이 제약 조건을 어떻게 추가하고 어떤 변경을 해야 할까요?
이러한 변경을 위해 example2 폴더를 사용하겠습니다. 안타깝게도 a! == 1은 유효한 제약 조건이 아니기 때문입니다. [상수, 덧셈, 곱셈, 방정식 검사로 구성되지 않았기 때문입니다. "어떤 것이 아니다"는 어떻게 표현할까요?
직관적이지 않은 이러한 유형의 문제는 회로를 작성하는 기술이 필요한 부분입니다. 이 기술을 개발하는 데는 시간이 걸리고 이 초기 튜토리얼의 범위를 벗어나지만 다행히도 좋은 자료가 많이 있습니다. [25]
그러나 몇 가지 일반적인 관용구가 있습니다. 기본 개념은 IsZero() 템플릿을 사용하여 표현식이 0과 같은지 확인하는 것입니다. 참 값이면 1을 출력하고 거짓 값이면 0을 출력합니다.
진리 테이블[^26]을 사용하여 가능한 값을 표시하는 것이 도움이 되는 경우가 많습니다. 다음은 IsZero()에 대한 진리 테이블입니다:
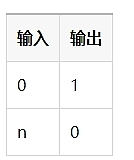
이것은 매우 유용한 빌딩 블록으로 Circom의 라이브러리인 circomlib에 포함되어 있습니다. circomlib에는 다른 유용한 구성 요소도 많이 있습니다. [^27]
npm 프로젝트(JavaScript)를 생성하고 종속성으로 추가하여 포함할 수 있습니다. example2 폴더에서 이 단계를 수행했습니다. 관련 모듈을 가져오려면 example2.circom 상단에 다음 줄을 추가합니다:
include "circomlib/circuits/comparators.circom";
IsZero()를 사용하여 a 또는 b가 1인지 확인할 수 있습니다. 다음 줄이 포함되도록 example2.circom 파일을 수정합니다:
just generate_proof example2
just verify_proof example2
이 경우에도 예상대로 증명을 생성하고 검증합니다.
example2/input.json의 입력을 1과 33으로 변경하고 위의 명령을 실행하려고 하면 어설션 오류가 발생합니다. 즉, 입력이 제약 조건을 위반하기 때문에 Circom에서 증명을 생성하지 못합니다.
이제 전체 과정을 두 번 거쳤으니 한 걸음 물러나서 모든 조각이 어떻게 맞물려 있는지 살펴봅시다.
<그림 style="text-align: 가운데;">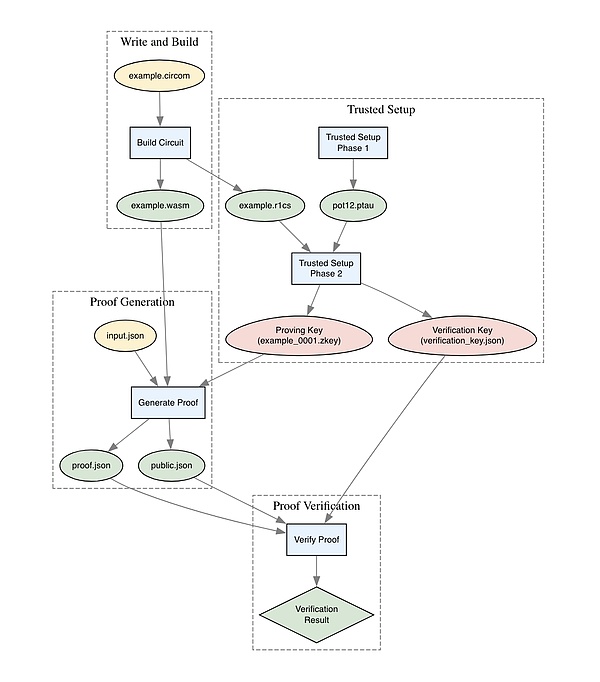
그렇다면 상황이 조금 더 명확해지기 시작했을 것입니다. 이제 회로를 좀 더 유용하게 만들기 위해 조금 더 강화해 보겠습니다.
왜 1단계가 아닌 example2의 2단계를 실행해야 할까요?
지난 예제의 주요 문제점은 무엇이었으며 어떻게 해결했나요?
코드: 증명을 생성할 수 없을 때까지 example2를 완성하세요.
위 회로를 통해 두 비밀 값의 곱을 알고 있음을 보여주었습니다. 이것만으로는 그다지 유용하지 않습니다. 실제 세계에서 유용한 것은 _디지털 서명 체계_입니다. 이를 통해 특정 메시지를 작성했음을 다른 사람에게 증명할 수 있습니다. 이를 위해 ZKP를 어떻게 사용할 수 있을까요? 이를 위해서는 먼저 몇 가지 기본 개념을 이해해야 합니다.
짧은 휴식을 취하고 좋아하는 음료 한 잔을 마시기 좋은 시간입니다.
디지털 서명은 이미 존재하며 디지털 시대에는 어디에나 존재합니다. 현대 인터넷은 디지털 서명 없이는 작동할 수 없습니다. 일반적으로 디지털 서명은 공개 키 암호화를 사용하여 구현됩니다. 공개 키 암호화에는 개인 키와 공개 키가 있습니다. 개인 키는 본인만 사용하는 반면, 공개 키는 공개적으로 공유되며 사용자의 신원을 나타냅니다.
디지털 서명 체계는 다음과 같은 부분으로 구성됩니다:
키 생성: 개인 키와 그에 해당하는 공개 키를 생성합니다
서명: 개인 키와 메시지를 사용하여 서명을 생성
서명 검증: 메시지가 해당 공개 키로 서명되었는지 확인
구체적인 내용은 다르지만, 위에서 설명한 키 생성 알고리즘과 우리가 작성한 프로그램은 하나의 공통 요소를 공유하는데, 둘 다 _일방향 함수를 사용한다는 점입니다. 더 구체적으로 말하면 _트랩 함수_를 사용한다는 점입니다. 함정 함수는 빠지기는 쉽지만 (숨겨진 사다리를 찾지 못하면) 빠져나오기는 어려운 함정입니다[^30].
<그림 style="text-align: 가운데;">
공개키 암호화를 사용하면 개인키에서 공개키를 만드는 것은 쉽지만 그 반대의 경우는 매우 어렵습니다. 이전 절차도 마찬가지입니다. 두 비밀 번호가 매우 큰 소수인 경우, 그 곱을 원래 값으로 다시 변환하는 것은 매우 어렵습니다. 최신 공개 키 암호화는 일반적으로 하단에 _타원 곡선 암호화_를 사용합니다.
전통적으로 이러한 디지털 서명 체계와 같은 암호화 프로토콜을 만들려면 많은 작업이 필요하며, 교묘한 수학이 포함된 특정 프로토콜을 만들어야 합니다. 저희는 그렇게 하고 싶지 않았습니다. 대신 ZKP를 사용하여 동일한 결과를 얻을 수 있는 프로그램을 작성하고자 했습니다.
이 대신에:[^31]
<그림 style="text-align: 가운데;">
우리는 단지 원하는 증명을 생성하고 원하는 증명을 생성하고 그 증명을 검증하는 프로그램을 작성하고 싶습니다.
타원 곡선 암호화를 사용하는 대신 _해시 함수_와 _커미트먼트_라는 두 가지 더 간단한 도구를 사용하겠습니다.
해시 함수는 단방향 함수이기도 합니다. 예를 들어, 명령줄에서 SHA-256 해시 함수를 다음과 같이 사용할 수 있습니다:
commitment = hash(some_secret)
서명 nbsp;서명 = hash(some_secret, message)
이 시점에서 몇 가지 질문이 있을 수 있습니다. 머릿속에 떠오르는 몇 가지 의문을 해결해 보겠습니다.
첫째, 이것이 왜 작동하며 왜 ZKP가 필요한가요? 누군가 증명을 검증할 때는 약속, 메시지, 서명에만 접근할 수 있습니다. 비밀을 공개하지 않고 약속이 비밀에 해당하는지 직접 확인할 수 있는 방법은 없습니다. 이 경우 증명을 생성할 때 비밀을 "공개"하기 때문에 비밀이 안전하게 유지됩니다.
두 번째로, 공개 키 암호화 대신 ZKP 내부에서 이러한 해시 함수와 약속을 사용하는 이유는 무엇인가요? ZKP 내에서 공개 키 암호화를 사용할 수 있으며, 그렇게 하는 데에는 타당한 이유가 있습니다. 제약 조건 측면에서 보면 위의 옵션보다 구현하는 데 훨씬 더 많은 비용이 듭니다. 따라서 위의 옵션보다 더 느리고 복잡합니다. 다음 섹션에서 살펴보겠지만 해시 함수의 선택은 매우 중요합니다.
마지막으로, 이미 공개 키 암호화가 있는데 왜 ZKP를 사용할까요? 이 간단한 예시에서는 ZKP를 사용할 필요가 없지만, 이 글의 시작 부분에서 언급한 그룹 서명 예시와 같이 더 흥미로운 애플리케이션을 위한 빌딩 블록 역할을 합니다. 결국, 우리는 _프로그래밍 암호화_를 원합니다.
많네요! 다행히도 한 고비는 넘겼습니다. 이제 코딩을 시작하겠습니다. 처음에 위의 내용을 완전히 이해하지 못하더라도 걱정하지 마세요. 이러한 추론 방식에 익숙해지려면 시간이 좀 걸릴 것입니다.
example3 디렉토리에서 작업을 시작하겠습니다.
디지털 서명을 구현하기 위해 가장 먼저 해야 할 일은 키를 생성하는 것입니다. 이는 공개 키 암호화에서 개인 키와 공개 키에 해당합니다. 키는 신원(증명자인 사용자)에 해당하므로 각각 identity_secret와 identity_commitment라고 부르겠습니다. 이들은 함께 신원 쌍을 형성합니다.
이것들은 우리가 서명하는 메시지가 있는 회로의 입력으로 사용됩니다. 공개 출력으로 서명, 커미트먼트, 메시지를 갖게 됩니다. 이를 통해 누군가가 서명이 실제로 올바른지 확인할 수 있습니다.
회로의 입력으로 ID 쌍이 필요하므로 이를 별도로 생성합니다:just generate_identity
이것은 다음과 같은 결과를 생성합니다:
include
포세이돈 해시 템플릿은 다음과 같이 사용됩니다:
< code> component main {public [identity_commitment, message ]} = SignMessage();
기본적으로 우리 회로에 대한 모든 입력은 비공개입니다. 이를 통해 identity_commitment와 message를 공개로 명시적으로 표시합니다. 이는 공개 출력의 일부가 된다는 의미입니다.
이 정보를 통해 example3.circom 회로를 완성할 수 있는 충분한 지식을 갖추게 될 것입니다. 여전히 문제가 해결되지 않는다면 전체 코드는 example3-solution.circom를 참조하세요.
이전과 마찬가지로 회로를 빌드하고 신뢰할 수 있는 설정의 2단계를 실행해야 합니다:
{
"identity_. secret": "21879[...] 7915",
"message": "42"
"}
신원 쌍을 자유롭게 변경할 수 있습니다. 를 just generate_identity를 사용하여 직접 생성한 ID 쌍으로 자유롭게 변경할 수 있습니다. 결국, 여러분은 자신의 신원을 비밀로 유지하고 싶을 것입니다!
메시지가 문자열로 참조된 숫자("42")일 뿐이라는 것을 알 수 있습니다. 안타깝게도 제약 조건이 수학적으로 작동하는 방식(선형 대수 및 _산술 회로_ 사용)으로 인해 문자열이 아닌 숫자만 사용할 수 있습니다. 회로가 내부적으로 지원하는 유일한 연산은 덧셈과 곱셈과 같은 기본적인 산술 연산입니다. [^37]
이제 증명을 생성하고 검증할 수 있습니다:
["48968 [...] 5499", "48269 [...] 7915", "42"]
이것은 각각 서명, 약속, 메시지에 해당합니다.
조심하지 않으면 어떻게 일이 잘못될 수 있는지 살펴봅시다. [38]
먼저, input.json에서 ID 약속을 임의의 것으로 변경하면 어떻게 될까요? 더 이상 증명을 생성할 수 없다는 것을 알 수 있습니다. 이는 회로 내부에서 여전히 신원 약속을 확인하고 있기 때문입니다. 신원 비밀과 약속 사이의 관계를 유지하는 것이 중요합니다.
둘째, 출력에 메시지를 포함하지 않으면 어떻게 되나요? 우리는 증명을 받고 검증을 받습니다. 하지만 메시지는 _무엇이든_ 될 수 있으므로 실제로 특정 메시지를 보냈다는 것을 증명하지는 못합니다. 마찬가지로 공개 출력에 신원 약속을 포함하지 않으면 어떻게 될까요? 즉, 신원 약속은 무엇이든 될 수 있으므로 실제로 누가 메시지에 서명했는지 알 수 없습니다.
생각 연습으로 이 두 가지 주요 제약 조건 중 하나를 생략하면 어떻게 될지 생각해 보세요.
identity_commitment === identityHasher.out
서명 <== signatureHasher.out
축하합니다, 이제 암호화를 프로그래밍하는 방법을 알았습니다! [^39]
연습디지털 서명 체계의 세 가지 구성 요소는 무엇인가요?
포세이돈과 같은 "ZK 친화적 해시 함수"를 사용하는 목적은 무엇인가요?
프로미스란 무엇인가요? 디지털 서명 체계에서 어떻게 사용할 수 있나요?
아이덴티티 약속과 메시지를 공개로 표시하는 이유는 무엇인가요?
신원 약속과 서명 제약 조건이 필요한 이유는 무엇인가요?
코드: 증명을 생성하고 검증할 때까지 <코드>예시3를 작성하세요.
위와 같은 디지털 서명 체계와 이 글에서 살펴본 몇 가지 요령을 사용하면 글의 서두에 언급한 그룹 서명 체계를 구현하는 데 필요한 모든 도구를 갖추게 됩니다. [^40]
스켈레톤 코드는 <코드>예제4에 있습니다. 5~10줄의 코드만 있으면 됩니다. 유일한 새로운 구문은 대부분의 다른 언어와 동일한 방식으로 작동하는 for 루프입니다. [^41].
이 회로를 사용하면 다음을 수행할 수 있습니다.
메시지에 서명
세 가지 중 하나임을 인증(신원 확인)
하지만 어느 쪽인지 밝히지 않음
퍼즐이라고 생각하시면 됩니다. 핵심 인사이트는 기본적으로 산술적인 표현으로 요약됩니다. 가능하면 종이 위에서 풀어보세요. 막히면 이전과 마찬가지로 해결 방법을 확인하세요.
마지막으로, 추가적인 도전을 원한다면 다음과 같이 몇 가지 확장 방법을 시도해 보세요.
그룹에 원하는 만큼 많은 사람을 허용하세요
새 회로 <코드>공개를 구현하여 다음을 증명합니다. 특정 메시지에 서명하지 않았음을 증명하는 새로운 회로 <코드>거부 구현
기존 도구를 사용하여 이러한 암호화 프로토콜을 만드는 것은 엄청난 작업이며, 많은 전문 지식이 필요합니다. [ZKP를 사용하면 이러한 문제를 프로그래밍 작업으로 처리하여 오후에 효율적이고 위험하지 않게 만들 수 있습니다. 이것은 우리가 할 수 있는 일의 빙산의 일각에 불과합니다.
그룹 서명과 일반 서명의 차이점은 무엇인가요? 어떻게 사용할 수 있나요?
이 질문은 선택 사항이며 더 많은 작업이 필요합니다.
IsZero()가 어떻게 구현되는지 알아보세요.
코드: 위의 그룹 서명 체계를 완성합니다(예제4 참조).
코드: 위의 그룹 서명 예제를 확장하여 더 많은 사람을 허용하고 reveal 및/또는 deny 회로를 구현합니다.
18세임을 증명하기 위해 "ZK 신원" 시스템을 어떻게 설계하시겠습니까? 증명하고 싶은 다른 속성은 무엇인가요? 높은 수준에서 이를 어떻게 구현할 것이며 어떤 어려움이 있을까요? 기존 솔루션을 조사하여 구현 방식을 더 잘 이해하세요.
이더와 같은 퍼블릭 블록체인의 경우, 더 빠르고 저렴하며 더 많은 트랜잭션을 허용하기 위해 레이어 2(L2)를 사용하기도 합니다. ZKP를 사용하여 L2를 어떻게 설계할 수 있을까요? 여러분이 생각하는 몇 가지 과제를 설명하세요. 기존 솔루션을 조사하여 구현 방식을 더 잘 이해합니다. ## 결론
이 튜토리얼 소개에서는 기본적인 영지식 증명(ZKP)을 처음부터 작성하고 수정하는 방법을 익혔습니다. 프로그래밍 환경을 설정하고 기본 회로를 작성했습니다. 그런 다음 그럴듯한 설정을 수행하고 증명을 생성하고 검증했습니다. 몇 가지 문제를 파악하고 회로를 개선하면서 변경 사항을 테스트했습니다. 그 후 해시 함수와 약속을 사용하여 기본적인 디지털 서명 체계를 구현했습니다.
영지식 증명 없이는 구현하기 어려운 그룹 서명을 구현할 수 있을 만큼의 기술과 도구도 배웠습니다.
영지식 증명을 작성하는 데 필요한 정신적 모델을 더 잘 이해하고 실제로 편집-실행-디버그 주기를 더 잘 이해할 수 있기를 바랍니다. 이는 어떤 기술 스택을 사용하든 앞으로 작성하게 될 다른 영지식 증명 프로그램을 위한 좋은 토대가 될 것입니다.
초고를 읽고 피드백을 제공해 주신 Hanno Cornelius, Marc Köhlbrugge, Michelle Lai, lenilsonjr, Chih-Cheng Liang에게 감사드립니다.
부르바키 회의 1938 - 위키미디어를 통해 알 수 없음, 퍼블릭 도메인[11]
트랩도어 거미 - P.S. Foresman, 퍼블릭 도메인 위키미디어](https://commons.wikimedia.org/wiki/File:Trapdoor_(PSF\"위키미디어").png)
킹슬리 락박스 - P.S. . 포레즈맨, 퍼블릭 도메인, 위키미디어 경유[13]
참고
[1] AI 번역기 : https://learnblockchain.cn/people/19584
[2] 번역팀: https://learnblockchain.cn/people/412
[3] learnblockchain.co.uk /article...: https://learnblockchain.cn/article/9178
[4]제로 지식에 대한 친절한 소개: https://learnblockchain.cn/article/6184
[5] git 리포지토리: https://github.com/oskarth/zkintro-tutorial
[6] git 리포지토리: https://github.com/oskarth/zkintro-tutorial
[7]여기: https://docs.circom.io/getting-started/installation/
[8]zkrepl.dev: https://zkrepl.dev/
[9]공식 문서: https://docs.circom.io/circom-language/signals/
[10]친숙한 영지식 증명 소개: https://learnblockchain.cn/article/6184
[11]위키미디어: https://commons.wikimedia.org/wiki/File:Bourbaki_congress1938.png
[12]위키미디어: https://commons.wikimedia.org/wiki/File:Hartmann_zebras_hobatereS.jpg< /em>
[13]위키미디어: https://commons.wikimedia.org/wiki/File. Kingsley_lockbox.jpg
[14]AI 번역기: https://learnblockchain. cn/people/19584
[15] 여기: https://github.com/lbc-team/. 개척자/블롭/마스터/번역/9178.md
[16]^2]: 참조: [ 연방주의자 논문 (위키백과): https://en.wikipedia.org/wiki/The_Federalist_Papers#Authorship
[17]^3]: [부르바키 (위키백과) 참조: https://en.wikipedia.org/wiki/Nicolas_Bourbaki#Membership< /p>
[18]^8]: 상상할 수 있듯이 제약 조건을 작성하는 것은 상당히 어렵습니다. Circom의 제약 조건에 대한 자세한 내용은 [https://docs.circom.io/circom-language/constraint-generation/: https://docs.circom.io/circom-language/ constraint-generation/
[19]^12]: 선형 제약조건은 덧셈만으로 표현할 수 있는 것으로 선형 조합으로 표현할 수 있습니다. 이는 상수를 사용한 곱셈과 동일합니다. 주목해야 할 점은 선형 제약 조건이 비선형 제약 조건보다 간단하다는 것입니다. 자세한 내용은 [제약 조건 생성: https://docs.circom.io/circom-language/constraint-generation/
< span style="font-size: 14px;">[20]산술 회로: https://docs.circom.io/background/background/#arithmetic-circuits
[21]^13]: 수학적으로, 우리가 하고 있는 것은 Az * Bz = Cz< 가 유지되며, 여기서 Z=(W,x,1). A,B 및 C입니다. 는 행렬이고,W는 증인(비공개 입력)이며,x는 공개 입력/출력입니다. 이를 알아두면 유용하지만, 회로를 작성할 때 이를 반드시 이해할 필요는 없습니다. 자세한 내용은 [1등급 제약 조건 시스템: https://docs.circom.io/background/background/#rank-1-constraint-system
[22]^15]: Friendly Intro 기사에서 언급했듯이, 지캐시가 주최한 2016년 행사에 대한 좋은 일반인용 팟캐스트가 있으며, [여기: https://>에서 찾아볼 수 있습니다. radiolab.org/podcast/ceremony
[23]^17]: 우리는 이를 N 중 1의 신뢰 모델이라고 부릅니다. 신뢰 모델에는 여러 가지가 있지만, 가장 익숙한 것은 다수가 올바른 결정을 내릴 것이라고 믿는 다수결 원칙입니다. 이는 기본적으로 민주주의와 다수결 투표가 작동하는 방식입니다. [: #user-content-fnref-17
[24]^22]: _암호화 난이도 가정_이라고도 합니다. 계산 난이도 가정(위키백과) 참조: https://en.wikipedia.org/wiki/Computational_hardness_assumption#Common_cryptographic_hardness_assumptions
[25]^23]: 자세한 내용은 [https://en.wikipedia.org/wiki/]를 참조하세요. 정수_인수분해: https://en.wikipedia.org/wiki/Integer_factorization
[26]^24]: _asserts_를 추가할 수 있지만, 이는 실제로 제약 조건이 아니며 입력을 정리하는 데만 사용됩니다. 작동 방식에 대한 자세한 내용은 [https://docs.circom.io/circom-language/code-quality/code-assertion/: https://docs.circom.io/circom-language/code-을 참조하세요. quality/code-assertion/
[27]https://www.chainsecurity.com/ blog/circom-assertions-misconceptions-and-deception: https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and- deceptions
[28]^25]: 0xPARC의 이 자료는 글쓰기 기술에 대해 더 자세히 알아보고 싶다면 훌륭한 자료입니다. Circom) 회로: [https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/: https://learn.0xparc.org/materials/circom/ learning-group-1/circom-1/
[29]^26]: 쓰기 제약의 특성으로 인해 이러한 상황이 자주 발생합니다. https://en.wikipedia.org/wiki/Truth_table: https://en.wikipedia.org/wiki/Truth_table
[30]^27]: circomlib에 대한 자세한 내용은 [https://github.com/iden3/circomlib: https://github.com/ iden3/circomlib
[31]^28]: 참조: [https://github.com/iden3 /circomlib/blob/master/circuits/comparators.circom: https://github.com/iden3/circomlib/blob/master/circuits/comparators.circom< /em>
[32]^29]: 사람들은 종종 프로젝트 간에 이것을 공유합니다 ptau 파일을 프로젝트 간에 공유하여 보안을 강화합니다. 자세한 내용은 [https://github.com/privacy-scaling-explorations/perpetualpowersoftau: https://github.com/privacy-scaling- explorations/perpetualpowersoftau
[33] https://github.com/ iden3/snarkjs: https://github.com/iden3/snarkjs
[34]^30] 여기서 사다리는 우리가 '어려운' 반대 방향으로 나아갈 수 있게 해주는 일종의 가치를 나타냅니다. 사다리를 자물쇠로 생각할 수도 있습니다. 자물쇠는 쉽게 잠글 수 있지만 열쇠가 없으면 열기가 어렵습니다. 트랩도어 기능은 보다 공식적으로 정의된 [https://en.wikipedia.org/wiki/Trapdoor_function: https://en.wikipedia.org/wiki/Trapdoor_function
[35]^31]: Wikipedia의 스크린샷. ECDSA(위키백과) 참조: https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Signature_verification_algorithm
[36]^38]: 실제 디지털 서명 체계에서는 여러 메시지를 주고받을 때 암호화 난수를 도입할 수도 있습니다. 이는 누군가가 나중에 동일한 서명을 재사용할 수 있는 리플레이 공격을 방지하기 위한 것입니다. https://en.wikipedia.org/wiki/Replay_attack: https://en.wikipedia.org/wiki/Replay_attack
[37]^40]: ZKP에서 그룹 서명을 구현하는 것은 0xPARC에서 영감을 얻었으며, [https://0xparc.org/blog/zk-group-sigs: https:// 0xparc.org/blog/zk-group-sigs
[38]^41]: 참조: [https:// docs.circom.io/circom-language/control-flow/: https://docs.circom.io/circom-language/control-flow/
[39]^42]: 반면, [https://eprint.iacr.org/2015/043.pdf: https://eprint]과 같은 그룹 서명을 구현하는 논문은 다음과 같습니다. iacr.org/2015/043.pdf
SAFT와 SAFE는 간단하고 유연하며 효율적으로 자금을 조달할 수 있는 방법이며, 몇 페이지에 불과하며, SAFT는 통화권 자금 조달에, SAFE는 주식 자금 조달에 사용됩니다.
 JinseFinance
JinseFinance소프트웨어가 주도하고 커뮤니티가 관리하는 토큰 네트워크는 전 세계 경제와 사회에 영향을 미칠 수 있는 엄청난 잠재력을 가지고 있습니다.
 JinseFinance
JinseFinance골든 파이낸스는 게임, 디파이, DAO, NFT, 메타버스 산업에 대한 가장 빠른 최신 뉴스를 제공하는 골든 웹 3.0 데일리를 발행합니다.
 JinseFinance
JinseFinance케이맨 제도 대 바하마: FTX 스캔들이 두 관할권에 미친 영향.
 Beincrypto
Beincrypto파산한 암호 헤지 펀드는 한때 $100M NFT 수집을 목표로 했지만 현재 가치는 $1M 미만일 수 있습니다.
 Coindesk
Coindesk네, 사실입니다. FBI는 최근 DeFi를 대상으로 하는 사이버 범죄 익스플로잇에 대해 경고를 발령했습니다. 실제로 DeFi 플랫폼은 ...
 Bitcoinist
BitcoinistCointelegraph와의 인터뷰에서 MP Isola는 지브롤터의 암호화 규제 환경과 비트코인에 대한 그의 관심에 대해 자세히 설명했습니다.
 Cointelegraph
Cointelegraph벨기에 국회의원은 국내 인기 암호화폐 거래 플랫폼인 Bit4You를 통해 월급 5,500유로를 비트코인으로 전환할 예정입니다.
 Cointelegraph
Cointelegraph키르기스스탄은 암호화폐 거래소와 채굴을 규제하지만 암호화폐 유통에 관한 법률은 없습니다.
 Cointelegraph
Cointelegraph키르기스스탄은 암호화폐 거래소와 채굴 산업을 규제했지만 국내 암호화폐 유통을 규제하는 법은 없습니다.
 Cointelegraph
Cointelegraph