Summa
We generally hold cryptocurrency and often buy, sell, and exchange currencies on centralized exchanges. operate. Transactions on centralized exchanges are very convenient and fast. In the more than ten years since the issuance of Bitcoin, many centralized exchanges have emerged on the market, which greatly facilitates users’ cryptocurrency buying and selling operations. However, with the prosperity of centralized exchanges, fraud and malicious behavior such as withdrawing money and running away are common. Netflix has specially filmed a promotional video about the sudden collapse of the exchange and the mysterious death of the founder: Don’t trust anyone, the virtual currency mystery [1]. In particular, FTX's declaration of bankruptcy due to insolvency in 2022 shocked the world, and many users and fund companies suffered huge losses.
In fact, not only in the field of cryptocurrency, but also in other traditional fields, there are countless behaviors that deceive investors through accounting fraud. Such as the Enron incident that shocked the world at the beginning of the 21st century. Enron was selected as "America's Most Innovative Company" by Fortune magazine for six consecutive years. However, such a company with hundreds of billions of assets went bankrupt within a few weeks in 2002. Another example is Evergrande Company, which diverted the funds originally used to build buildings for other purposes. Eventually, countless owners were saddled with 30-year mortgage loans and waited for unfinished houses.
An important reason behind the endless fraud in many different fields is that the auditing and accounting work itself is not completely open and transparent, which creates huge room for corruption and cheating. . However, in order to protect the company's interests and investor privacy, key financial data cannot be completely open and transparent. Therefore, there has been no good solution to financial fraud except strengthening supervision. However, as zero-knowledge proof technology gradually matures, we can see that to a new solution.
If every user can verify whether some of their assets have financial fraud, then as long as there are enough verified users, then an organization wants to do financial fraud Fraud will be very difficult. And because the verification process is zero-knowledge, even if the third party intercepts the data during the network transmission of the verification data, he does not know what the user's real assets are. In this way, the verification process can be completely implemented in the network. Displayed publicly on the Internet. With the help of zero-knowledge proof technology, a considerable amount of audit work is no longer the patent of certain organizations like the Big Four accounting firms, and is conducted secretly behind closed doors. Rather, it is an open process in which any stakeholder can participate.
Summa[2] is a PSE research project that aims to use zk method to verify user assets. The following content of this article will briefly introduce the project and the technical implementation principles.
Contract
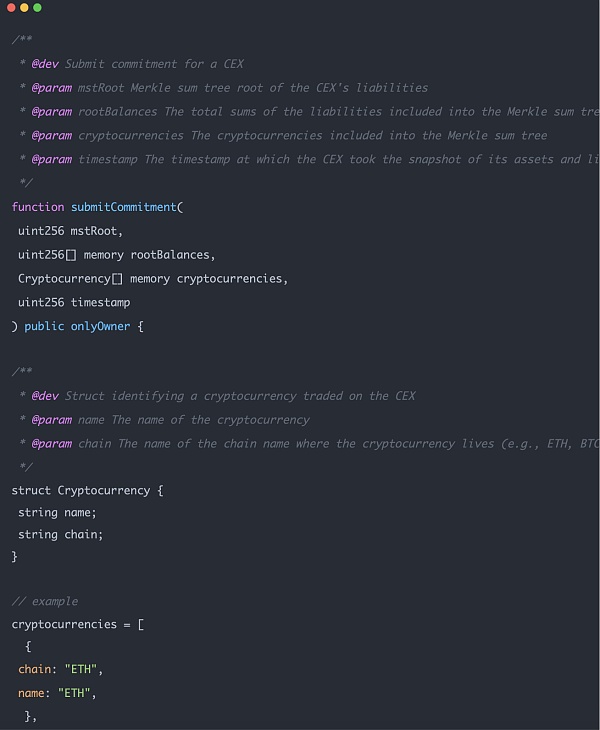
Summa’s overall data flow is shown in the figure. Smart contracts are mainly used here to store and verify some public data. It is not necessarily strongly bound to Ethereum, even if it is deployed on other blockchains such as Solana in the future (as long as Halo2 has corresponding blockchain support, some contracts in this project are generated by Halo2 proof[3 ]).

Custodian in the picture represents a centralized exchange. The contract is deployed on the chain by the exchange, and the contract ownership belongs to the exchange. Public data can only be submitted by the exchange. Public data consists of two parts. One part is the basic information of the chain controlled by the exchange and digital signatures.

p>
The second part is the information of the assets on the chain, including the root hash of the Merkle sum tree, and the root balance (the specific number of assets on the chain, such as how many BTC), This part of the data will be used for the instance input of zk proof.
p>
Both parts of the data are easily publicly available on the chain (except for the root hash). It would be difficult for exchanges to cheat on this data. Anyone can compare the data stored in the contract with the actual data results on the blockchain address.
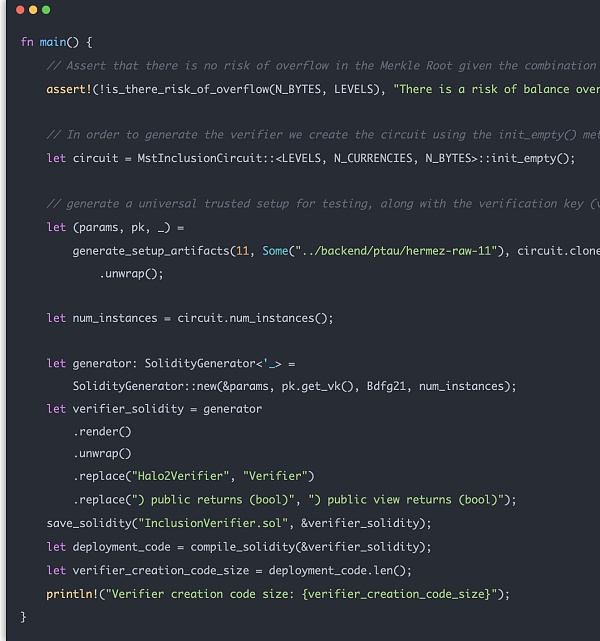
Proof generation is currently generated by the exchange. The user submits key information that needs to be verified to the exchange, and then the exchange generates the proof and returns it to the user. Users can request the smart contract with this proof, and the contract will verify the proof.
Finally, Proof Verify is where the user interacts directly with the contract. This part of the contract is translated into Solidity code by the Halo2 circuit and then deployed on the chain as a separate verification contract.
p>
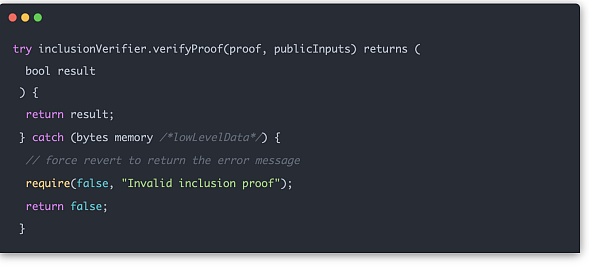
In actual use, proof can be passed in to calculate and verify on the chain.
p>
The following code example is the function used in the actual Hash operation. You can see that the entire hash calculation itself does not use bit operations, only addition and multiplication calculations, which is zk friendly.
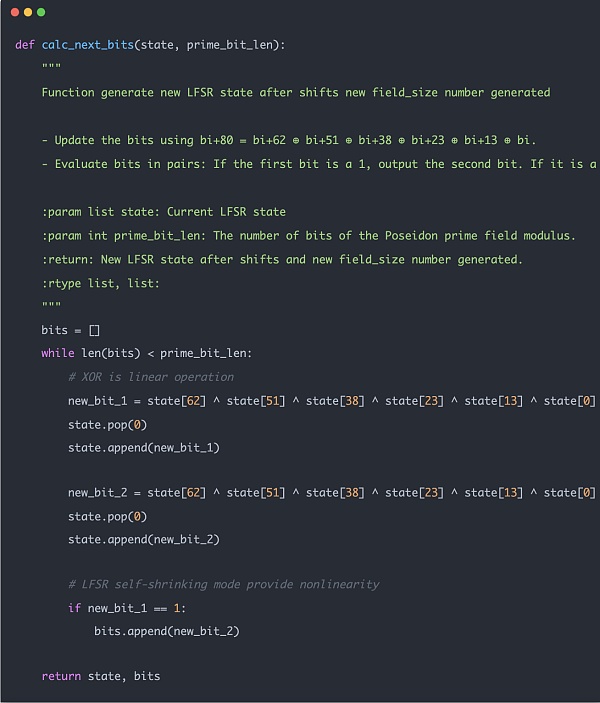
p>
The difference between zk data calculation and traditional program calculation is that zk data must be calculated in a finite domain. When constructing the Merkle Tree, ensure that each node data cannot exceed the finite domain. It is very necessary. For this reason, the data must be range checked before calculation so that the data overflows.
The general principle of range check is similar to the example below. First, for the input data, use 8 bits as the length unit and cut out multiple copies to facilitate future subtraction operations. Then every time you perform next numerical calculation, follow the calculation steps in the example below. When the range check circuit makes constraints, it actually makes constraints based on the intermediate result diff = z_cur - z_next * Expression::Constant(Fp::from(1 << 8)), requiring diff As long as it's within 8 digits. In this way, a 32-bit data constraint only requires 4 computing cells and 256 lookup tables. In the future, the instance constraint with the highest bit being 0 is enough. If it were not designed in this way, simply doing a range check of 32-bit values would require a sized lookup table. Obviously, such a circuit would be too large and cannot be applied in practice.
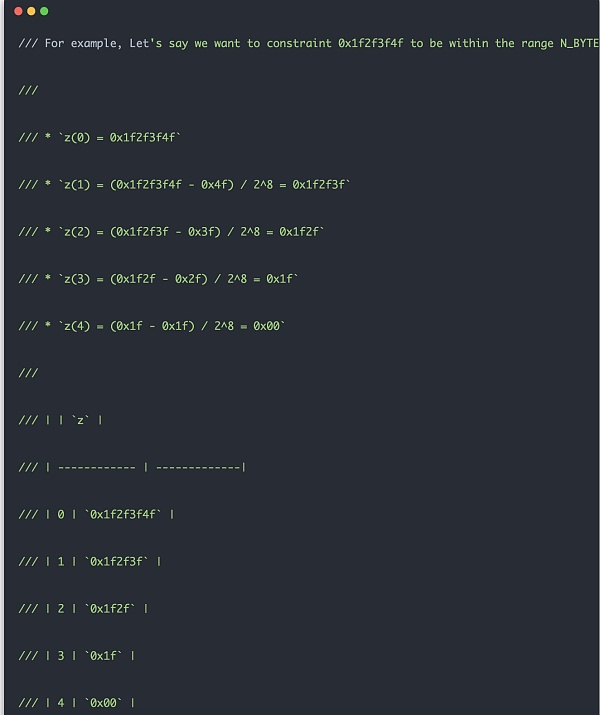
p>
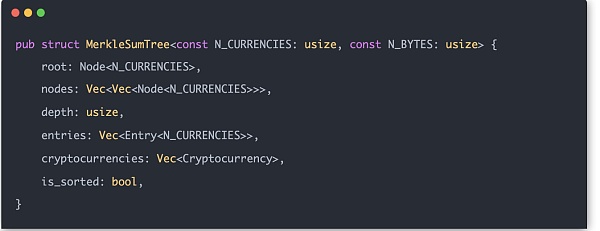
With these auxiliary structures, the Merkle Sum Tree can be formally constructed. Each user input data is called Entry, and its structure is:
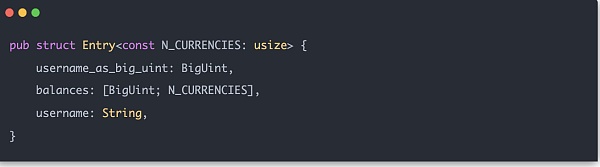
The hash calculation method of the middle node of Merkle Tree is H(LeftChild.balance[0 ] + RightChild.balance[0], LeftChild.balance[1] + RightChild.balance[1], ..., LeftChild.balance[N_CURRENCIES - 1] + RightChild.balance[N_CURRENCIES - 1], LeftChild.hash, RightChild .hash), so the actual length of the vec array to be calculated is N_CURRENCIES + 2.
Let's build the entire Merkle Tree completely. The leaf node part is relatively simple, you only need to convert Entry to Node. Intermediate nodes need to be constructed layer by layer, and the value of each intermediate node is related to the value of the left subtree and right subtree of the next layer. Finally, put the calculated intermediate node results into the tree array:
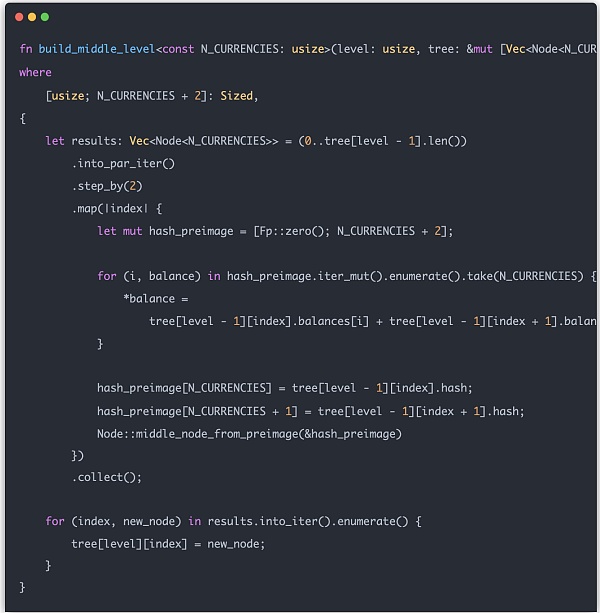
Next we use Merkle Tree to build zk proof. What zk wants to prove is that a user's entry is indeed on the Merkle Tree. Therefore, we first need to formulate a specific entry index and generate the data structure required for zk proof based on Merkle Tree.
p>
We can cleverly achieve the constraint effect of making the entire equation equal to 0 by setting 0 and 1.
Sponsored Business Content
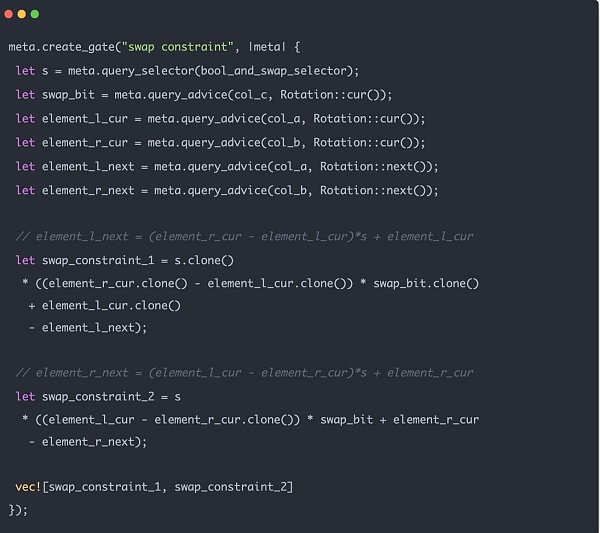
Merkle Tree zk constraints mainly have two parts. One part is the swap constraint to ensure that when the exchange generates the proof, it is indeed generated in the true order of the above figure. The other part is the balance constraint, that is, the balance of the parent node does come from the sum of the left child node and the right child node. The sum constraint on balance is relatively simple. Here we focus on the swap constraint.
The Merkle zk tree data structure sibling_middle_node_hash_preimages we introduced before is an array and does not contain position information. Whether the position of the dotted box in the picture should be on the left or right side of the tree must be judged by the 0 and 1 of path_indices. Therefore, we must ensure that when the value is 0, the generated parent node is on the left, and its corresponding sibling node of the same level is on the right, and when it is 1, the opposite is true. When data is imported into the zk circuit, this logic can be easily implemented in code:
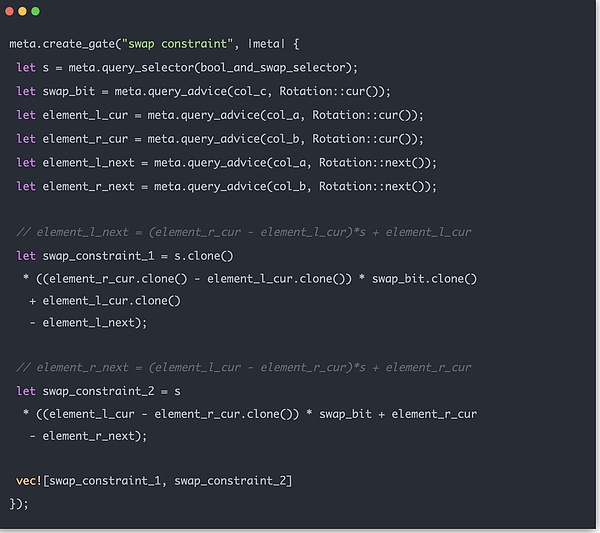
The overall Merkle Sum Tree zk proof process is to process the data layer by layer, and then convert the corresponding Position data input zk constraint circuit check. Build the entire Merkle Tree. The final output is the root node hash and the total balance, which should be consistent with the corresponding data in the contract. Use instance to verify the consistency. If all verifications are correct, the entire Merkle Tree proof work is concluded.
Solvency Verify
The process of generating proof is for the user to request the exchange and then trade The returned proof data is then verified by the user to the smart contract. At present, the project does not support users to bypass the exchange to generate proof by themselves, but it feels that it may be a direction that can be explored in the future. Proofs are generated directly by users rather than returned by exchanges. The entire halo2 proof circuit can be packaged into web assembly using rust, and then use ethers rs[7] to make the corresponding interactive API. The time complexity of Merkle Tree root verification is log(n). It may not take too much time for the user's device to be verified, which further enhances the security of decentralization.
Reference
[1]
Don’t trust anyone, virtual currency mystery: https://www.netflix.com/hk/title/81349029
[2]< /p>
Summa: https://github.com/summa-dev
[3]< /p>
Halo2 proof generated: https://github.com/privacy-scaling-explorations/halo2-solidity-verifier
[4]
Poseidon Hash: https://github.com/ingonyama-zk/poseidon-hash
< p style="text-align: left;">[5]
Parameter preparation phase and Hash operation phase: https://autoparallel.github.io/ overview/index.html
[6]
Linear-feedback shift register: https: //en.wikipedia.org/wiki/Linear-feedback_shift_register
[7]
ethers rs: https://github.com/gakonst/ethers-rs
Recommended reading
ZK Insights Series
zkp Study Notes
Wen Building Podcast
Research analysis series of articles
Uniswap fine translation series
Antalpha Labs is a non-profit Web3 developer community dedicated to promoting the innovation and application of Web3 technology by initiating and supporting open source software.
Official website:https://labs.antalpha.com
Twitter:https://twitter.com/Antalpha_Labs
Youtube:https:// www.youtube.com/channel/UCNFowsoGM9OI2NcEP2EFgrw
Contact us:hello.labs@antalpha.com
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Bitcoinworld
Bitcoinworld Numen Cyber Labs
Numen Cyber Labs Bitcoinist
Bitcoinist Cointelegraph
Cointelegraph Cointelegraph
Cointelegraph Cointelegraph
Cointelegraph