Lập trình bằng chứng không có kiến ​​thức - Circom, Groth16 bằng chứng xây dựng và xác minh

Nguồn: Cộng đồng Denglian

Giới thiệu về hướng dẫn ZKP dành cho lập trình viên đang làm việc.

Bạn có biết tại sao ngựa vằn lại có sọc không? Một giả thuyết cho rằng đó là sự ngụy trang. Khi ngựa vằn tụ tập lại với nhau, điều này khiến sư tử khó phân biệt con mồi hơn. Sư tử phải cách ly con mồi khỏi nhóm để truy đuổi nó[^1].

Con người cũng thích trốn trong đám đông. Một ví dụ cụ thể là khi nhiều cá nhân hoạt động như một đơn vị dưới một tên tập thể. Đây là cách các Giấy tờ Liên bang được tạo ra[^2]. Một ví dụ khác là Bourbaki, bút danh chung của một nhóm các nhà toán học người Pháp vào những năm 1930. Điều này dẫn đến việc viết lại hoàn toàn phần lớn toán học hiện đại, tập trung vào tính chặt chẽ và các phương pháp tiên đề[^3].

Trong thời đại kỹ thuật số, hãy tưởng tượng bạn đang tham gia một cuộc trò chuyện nhóm và muốn gửi một tin nhắn gây tranh cãi. Bạn muốn chứng minh rằng bạn là một trong số họ mà không tiết lộ ai. Làm thế nào chúng ta có thể thực hiện điều này trong lĩnh vực kỹ thuật số bằng cách sử dụng mật mã? Chúng ta có thể sử dụng thứ gọi là Chữ ký nhóm.

Theo truyền thống, chữ ký nhóm rất phức tạp về mặt toán học và khó thực hiện. Tuy nhiên, bằng cách sử dụng các bằng chứng không có kiến ​​thức (ZKP), bài toán này trở thành một nhiệm vụ lập trình đơn giản. Đến cuối bài viết này, bạn sẽ có thể viết chữ ký nhóm của riêng mình.

Giới thiệu

Bài viết này sẽ chỉ cho bạn cách viết một bằng chứng không có kiến ​​thức (ZKP) cơ bản từ đầu.

Khi tìm hiểu một nhóm công nghệ mới, chúng tôi muốn nắm vững chu trình chỉnh sửa-xây dựng-chạy càng nhanh càng tốt. Chỉ khi đó chúng ta mới có thể bắt đầu học hỏi từ kinh nghiệm của mình.

Trước tiên, chúng tôi sẽ yêu cầu bạn thiết lập môi trường của mình, viết một chương trình đơn giản, thực hiện cái được gọi là thiết lập đáng tin cậy, sau đó tạo và xác minh bằng chứng nhanh nhất có thể. Sau đó, chúng tôi sẽ xác định một số cách để cải thiện chương trình của mình, triển khai những cải tiến này và thử nghiệm chúng. Trong quá trình này, chúng tôi sẽ xây dựng một mô hình tinh thần tốt hơn để lập trình ZKP trong thực tế. Cuối cùng, bạn sẽ quen (bằng cách nào đó) với việc viết ZKP từ đầu.

Chúng tôi sẽ xây dựng từng bước một sơ đồ chữ ký đơn giản mà bạn có thể sử dụng để chứng minh rằng bạn đã gửi một tin nhắn cụ thể. Bạn sẽ có thể hiểu mã này làm gì và tại sao:

    # Sao chép kho lưu trữ và chạy quá trình chuẩn bị script
    git clone [email protected]:oskarth/zkintro-tutorial.git
    cd zkintro-tutorial
     
    # Duyệt qua nội dung của tệp này trước khi thực thi
    less ./scripts/prepare.sh
     ./scripts/prepare.sh

Chúng tôi khuyên bạn nên duyệt qua ./scripts/prepare.sh< /code> để xem nội dung này sẽ cài đặt những gì hoặc nếu bạn muốn cài đặt thủ công. Sau khi thực thi, bạn sẽ thấy Quá trình cài đặt hoàn tất và không có lỗi.

Nếu bạn gặp sự cố, vui lòng kiểm tra tài liệu chính thức mới nhất tại đây [7]. Sau khi hoàn tất, bạn nên cài đặt phiên bản sau (hoặc cao hơn):

    pragma circom 2.0.0;
    
    template Multiplier2 () {< Br ;
      c <== a * b;
    ; 
     
    thành phần main = Multiplier2();
Đây là chương trình đặc biệt của chúng tôi hoặc _mạch_. [^6] Phân tích từng dòng:
pragma Circom 2.0.0; - xác định Circom phiên bản được sử dụng 
template Multiplier() - Mẫu tương đương với các đối tượng trong hầu hết các ngôn ngữ lập trình ​​và là một dạng trừu tượng phổ biến
đầu vào tín hiệu a; - Đầu vào đầu tiên của chúng tôi, a; theo mặc định, đầu vào này là riêng tư
< li>
đầu vào tín hiệu b; - Đầu vào thứ hai của chúng tôi, b cũng được đặt ở chế độ riêng tư theo mặc định
< p> đầu ra tín hiệu b; - đầu ra của chúng tôi, c; đầu ra luôn ở chế độ công khai
c <= = a * b; - Điều này thực hiện hai việc: gán tín hiệu c cho và ràng buộc c phải bằng < Tích của code>a và b
comComponent main = Multiplier2() - khởi tạo thành phần Main của chúng ta
Dòng quan trọng nhất là c <== a * b;. Đây là nơi chúng tôi thực sự khai báo các ràng buộc. Biểu thức này thực sự là sự kết hợp của hai: <-- (gán) và === (ràng buộc đẳng thức). [^7] Các ràng buộc trong Circom chỉ có thể sử dụng các phép toán liên quan đến hằng số, phép cộng hoặc phép nhân. Nó buộc cả hai vế của phương trình phải bằng nhau. [^8]
Giới thiệu về các ràng buộc
Các ràng buộc hoạt động như thế nào? Trong ngữ cảnh giống như Sudoku, chúng ta có thể nói rằng ràng buộc là "một số từ 1 đến 9". Tuy nhiên, trong ngữ cảnh của Circom, đây không phải là một ràng buộc đơn lẻ mà là thứ chúng ta phải thể hiện bằng cách sử dụng một tập hợp các ràng buộc đẳng thức đơn giản hơn (===). [^9]
Tại sao lại thế này? Điều này liên quan đến các nguyên tắc toán học cơ bản. Về cơ bản, hầu hết ZKP đều sử dụng _mạch số học_, biểu thị phép tính đa thức. Khi làm việc với đa thức, bạn có thể dễ dàng đưa ra các hằng số, cộng chúng, nhân chúng và kiểm tra xem chúng có bằng nhau hay không. [^10] Các thao tác khác phải được thể hiện dưới dạng các thao tác cơ bản này. Bạn không cần phải biết chi tiết điều này để viết ZKP, nhưng sẽ rất hữu ích nếu biết những gì đang diễn ra bên trong. [^11]
Chúng ta có thể hình dung mạch điện như sau:
Xây dựng mạch của chúng tôi
Để bạn tham khảo, bạn có thể tìm thấy tệp cuối cùng trong example1-solution.circom. Để biết thêm chi tiết về cú pháp, hãy xem tài liệu chính thức [9]. 
Chúng ta có thể biên dịch mạch bằng cách chạy lệnh sau: 
Đây là lệnh gọi đơn giản tới circom để tạo example1.r1cs và example1.wasm gói tập tin. Bạn sẽ thấy nội dung tương tự như sau:
< code>    {
      "pi_a": ["15932[...]3948", "66284[.. .]7222", "1"],
      "pi_b": [
        ; ["17667[...]0525", "13094[...]1600"],
        ["12020[ ...]5738", "10182[...]7650"],
        ["1", "0"] 
      ],
      "pi_c":["18501[...]3969",  ;" 13175[...]3552", "1"],
      "giao thức": "groth16",
        "curve": "bn128"
    
Điều này dựa trên một số đối tượng toán học (ba Việc chứng minh được xác định dưới dạng các phần tử đường cong elip) pi_a, pi_b và pi_c. [^20] Nó cũng bao gồm siêu dữ liệu về giao thức (groth16) và _curve_ được sử dụng (bn128, một chi tiết triển khai toán học mà chúng tôi sẽ bỏ qua bây giờ). Điều này cho phép người xác minh biết phải làm gì với bằng chứng này để xác minh chính xác. 
Lưu ý rằng bằng chứng rất ngắn gọn; cho dù chương trình đặc biệt của chúng ta có phức tạp đến đâu thì nó cũng chỉ có kích thước như vậy. Điều này thể hiện đặc tính cô đọng của ZKP mà chúng ta đã thảo luận trong _Giới thiệu về Bằng chứng không có kiến ​​thức thân thiện_[10]. Lệnh trên cũng xuất ra _public đầu ra_ của chúng tôi:
Đây là danh sách tất cả các đầu ra công khai tương ứng với các nhân chứng và mạch của chúng tôi. Trong trường hợp này, có một đầu ra chung tương ứng với c:33. [^21]
Chúng ta đã chứng minh được điều gì? Chúng ta biết hai giá trị bí mật a và b và tích của chúng là 33. Điều này thể hiện thuộc tính Quyền riêng tư mà chúng ta đã thảo luận trong bài viết trước. 
Lưu ý rằng một bằng chứng không hữu ích khi đứng riêng lẻ, nó đòi hỏi một kết quả công khai sau đó. 
Bằng chứng xác minh
Tiếp theo, chúng ta hãy xác minh bằng chứng này. Chạy: 
chỉ verify_proof example1
Điều này yêu cầu xác minh khóa, kết quả công khai và bằng chứng. Với những điều này chúng ta có thể xác minh bằng chứng. Nó sẽ in "Bằng chứng đã được xác minh". Lưu ý rằng trình xác nhận không bao giờ chạm vào bất kỳ thông tin đầu vào riêng tư nào. 
Điều gì xảy ra nếu chúng ta thay đổi kết quả đầu ra? Mở example1/target/public.json, thay đổi 33 thành 34 và chạy lại lệnh trên. 
Bạn sẽ nhận thấy rằng bằng chứng không còn được xác minh nữa. Điều này là do bằng chứng của chúng ta không cho thấy rằng chúng ta có hai số có tích là 34. 
Xin chúc mừng, bạn hiện đã viết chương trình ZKP đầu tiên của mình, thiết lập niềm tin, tạo bằng chứng và cuối cùng đã xác minh nó! 
Bài tập
Hai thuộc tính chính của ZKP là gì và chúng có ý nghĩa gì? 
Vai trò của người chứng minh là gì và cô ấy yêu cầu những thông tin gì? Còn người xác nhận thì sao? 
Giải thích mục đích của dòng c <== a * b;. 
Tại sao chúng ta cần cài đặt đáng tin cậy? Chúng ta sử dụng sản phẩm của nó như thế nào? 
Mã: Hoàn thành example1 cho đến khi bạn tạo và xác minh bằng chứng. 
Lặp lại lần thứ hai
Với mạch trên, ta chứng minh được tích của hai số (bí mật). Điều này liên quan chặt chẽ đến bài toán phân tích hệ số nguyên tố, vốn là nền tảng của nhiều mật mã. [^22] Ý tưởng là nếu bạn có một số rất lớn thì rất khó tìm được hai số nguyên tố có tích bằng số lớn đó. Ngược lại, rất đơn giản để kiểm tra xem tích của hai số có bằng một số khác hay không. [^23]
Tuy nhiên, có một vấn đề lớn với mạch điện của chúng tôi. Bạn có thể nhìn thấy nó? 
Chúng ta có thể dễ dàng thay đổi đầu vào thành "1" và "33". Nghĩa là, một số c luôn là tích của 1 và c. Điều đó không ấn tượng lắm phải không? 
Điều chúng ta muốn làm là thêm một _constraint_ khác để a hoặc b không thể bằng 1. Bằng cách này, chúng tôi buộc phải thực hiện phân tích số nguyên thích hợp. 
Làm cách nào để thêm ràng buộc này và những thay đổi nào là cần thiết? 
Cập nhật mạch của chúng tôi
Chúng tôi sẽ sử dụng thư mục example2 cho những thay đổi này. Thật không may, chúng ta không thể chỉ viết a !== 1 vì đó không phải là một ràng buộc hợp lệ. [^24] Nó không bao gồm các hằng số, phép cộng, phép nhân và kiểm tra đẳng thức. Làm thế nào để chúng ta diễn đạt “cái gì đó không có”? 
Không thể hiểu ngay rằng loại vấn đề này là một phần của nghệ thuật viết mạch. Việc phát triển kỹ năng này cần có thời gian và nằm ngoài phạm vi của hướng dẫn ban đầu này; may mắn thay, có rất nhiều tài nguyên hữu ích để tham khảo. [^25]
Tuy nhiên, có một số thành ngữ phổ biến. Ý tưởng cơ bản là sử dụng mẫu IsZero() để kiểm tra xem một biểu thức có bằng 0 hay không. Nó xuất ra 1 cho giá trị đúng và 0 cho giá trị sai. 
Việc sử dụng bảng chân lý [^26] thường hữu ích để hiển thị các giá trị có thể có. Sau đây là bảng chân lý của IsZero():
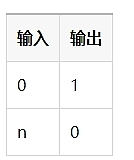
Đây là một khối xây dựng hữu ích đến mức nó được bao gồm trong thư viện circomlib của Circom. Có nhiều thành phần hữu ích khác trong circomlib. [^27]
Chúng ta có thể đưa nó vào bằng cách tạo một dự án npm (JavaScript) và thêm nó làm phần phụ thuộc. Trong thư mục example2, chúng tôi đã thực hiện việc này cho bạn. Để nhập các mô-đun có liên quan, chúng tôi thêm dòng sau vào đầu example2.circom:
include "circomlib/ Circuits/comparators.circom";
Sử dụng IsZero(), chúng ta có thể kiểm tra xem a hay b có bằng 1 hay không. Sửa đổi tệp example2.circom để bao gồm các dòng sau:
    just generate_proof example2
    just  verify_proof example2
Nó vẫn tạo và xác minh bằng chứng như mong đợi. 
Nếu chúng ta thay đổi đầu vào của example2/input.json thành 1 và 33 và thử chạy lệnh trên , chúng tôi Bạn sẽ thấy một lỗi xác nhận. Nghĩa là, Circom thậm chí sẽ không cho phép chúng tôi tạo bằng chứng vì dữ liệu đầu vào vi phạm các ràng buộc của chúng tôi. 
Sơ đồ đầy đủ
Bây giờ chúng ta đã thực hiện toàn bộ quá trình hai lần, hãy lùi lại một bước và xem tất cả các phần khớp với nhau như thế nào. 
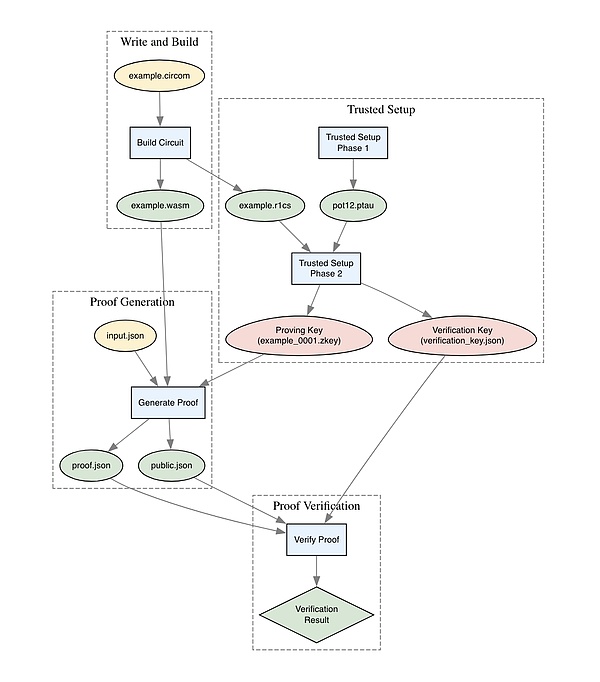
Hy vọng rằng mọi thứ đang bắt đầu ổn thỏa rõ ràng hơn một chút. Tiếp theo, hãy thực hiện một số cải tiến để làm cho mạch của chúng ta hữu ích hơn. 
Bài tập
Tại sao chúng ta phải chạy phần 2 của example2 giai đoạn thay vì giai đoạn 1? 
Vấn đề chính trong ví dụ trước là gì và chúng ta đã giải quyết nó như thế nào? 
Mã: Hoàn thành example2 cho đến khi bạn không thể tạo bằng chứng. 
Lần lặp thứ ba
Với mạch trên, ta đã chứng minh được tích của hai giá trị bí mật. Chỉ điều này thôi thì không hữu ích lắm. Trong thế giới thực, những gì hiệu quả là các sơ đồ chữ ký số. Thông qua nó, bạn có thể chứng minh cho người khác thấy rằng bạn đã viết một tin nhắn cụ thể. Làm cách nào chúng ta có thể sử dụng ZKP để đạt được điều này? Để đạt được điều này, trước tiên chúng ta phải đề cập đến một số khái niệm cơ bản. 
Bây giờ là thời điểm thích hợp để nghỉ ngơi một chút và thưởng thức một ly đồ uống yêu thích của bạn. 
Chữ ký số
Chữ ký số đã tồn tại và phổ biến trong thời đại kỹ thuật số của chúng ta. Internet hiện đại không thể hoạt động nếu không có chúng. Thông thường, những điều này được triển khai bằng cách sử dụng mật mã khóa công khai. Trong mật mã khóa công khai, bạn có khóa riêng và khóa chung. Khóa riêng chỉ dành cho bạn sử dụng, trong khi khóa chung được chia sẻ công khai và đại diện cho danh tính của bạn. 
Lược đồ chữ ký số bao gồm các phần sau: 
Tạo khóa: Tạo a Khóa riêng và khóa chung tương ứng
Chữ ký: Tạo chữ ký bằng khóa riêng và tin nhắn
 
Xác minh chữ ký: Xác minh rằng tin nhắn được ký bằng khóa chung tương ứng
Mặc dù các chi tiết cụ thể có vẻ khác nhau nhưng chương trình chúng tôi đã viết giống như thuật toán ở trên. Các thuật toán tạo khóa có chung một yếu tố: chúng đều sử dụng _hàm một chiều_, cụ thể hơn là _hàm bẫy_. Cửa sập là thứ dễ rơi vào nhưng khó trèo ra (trừ khi tìm được thang ẩn) [^30]. 
Đối với mật mã khóa công khai, Xây dựng lấy khóa công khai từ khóa riêng thì dễ nhưng làm ngược lại thì rất khó. Chương trình trước của chúng tôi cũng vậy. Nếu hai số bí mật là số nguyên tố rất lớn thì sẽ rất khó chuyển kết quả đó về giá trị ban đầu. Mật mã khóa công khai hiện đại thường sử dụng mật mã đường cong elip. 
Theo truyền thống, việc tạo ra các giao thức mật mã như các lược đồ chữ ký số này đòi hỏi rất nhiều công sức và đòi hỏi phải đưa ra một giao thức cụ thể liên quan đến một số phép toán thông minh. Chúng tôi không muốn làm điều này. Thay vào đó, chúng tôi muốn viết một chương trình sử dụng ZKP để đạt được kết quả tương tự. 
Thay vì thế này: [^31]
Chúng tôi chỉ muốn viết một chương trình tạo ra bằng chứng mà chúng tôi muốn và sau đó xác minh bằng chứng này. 
Hàm băm và cam kết
Thay vì sử dụng mật mã đường cong elip, chúng tôi sẽ sử dụng hai công cụ đơn giản hơn: _hash function_ và _commitments_. 
Hàm băm cũng là hàm một chiều. Ví dụ: từ dòng lệnh, chúng ta có thể sử dụng hàm băm SHA-256 như thế này:
    commitment = hash(some_secret)
    chữ ký = hash(some_secret,   tin nhắn)
Bạn có thể có một số câu hỏi vào lúc này. Hãy giải quyết một số câu hỏi mà bạn có thể có trong đầu. 
Đầu tiên, tại sao điều này lại hiệu quả và tại sao chúng ta cần ZKP? Khi ai đó xác minh bằng chứng, họ chỉ có quyền truy cập vào cam kết, tin nhắn và chữ ký. Không có cách nào trực tiếp để xác minh rằng một lời hứa có phù hợp với một bí mật mà không tiết lộ bí mật đó hay không. Trong trường hợp này, chúng tôi chỉ đơn giản là "tiết lộ" bí mật khi tạo ra bằng chứng, vì vậy bí mật của chúng tôi vẫn được an toàn. 
Thứ hai, tại sao các hàm băm và cam kết này được sử dụng bên trong ZKP thay vì mật mã khóa công khai? Bạn hoàn toàn có thể sử dụng mật mã khóa công khai bên trong ZKP và có những lý do chính đáng để làm như vậy. Xét về mặt hạn chế thì chi phí thực hiện của nó cao hơn rất nhiều so với các giải pháp trên. Điều này làm cho nó chậm hơn và phức tạp hơn so với ở trên. Như chúng ta sẽ thấy trong phần tiếp theo, việc lựa chọn hàm băm là rất quan trọng. 
Cuối cùng, tại sao lại sử dụng ZKP khi chúng ta đã có mật mã khóa công khai? Trong ví dụ đơn giản này, không cần sử dụng ZKP. Tuy nhiên, nó phục vụ như một khối xây dựng cho các ứng dụng thú vị hơn, chẳng hạn như ví dụ về chữ ký nhóm được đề cập ở đầu bài viết này. Rốt cuộc, chúng ta muốn _mật mã được lập trình_. 
Nhiều lắm đấy! May mắn thay, chúng tôi đã vượt qua được khó khăn. Hãy bắt đầu viết mã. Đừng lo lắng nếu ban đầu bạn không hiểu đầy đủ những điều trên. Phải mất một thời gian để làm quen với cách lập luận này. 
Quay lại mã
Chúng ta sẽ bắt đầu làm việc từ thư mục example3. 
Để triển khai chữ ký số, điều đầu tiên chúng ta cần làm là tạo khóa. Chúng tương ứng với khóa riêng và khóa chung trong mật mã khóa chung. Vì bí mật tương ứng với danh tính (bạn, người chứng nhận), nên chúng tôi sẽ gọi nó lần lượt là identity_secret và identity_commitment. Họ cùng nhau tạo thành một cặp nhận dạng. 
Những thứ này sẽ đóng vai trò là đầu vào của mạch, được sử dụng với thông điệp mà chúng ta muốn ký. Với tư cách là đầu ra công khai, chúng tôi sẽ có chữ ký, cam kết và thông điệp. Điều này sẽ cho phép ai đó xác minh rằng chữ ký thực sự chính xác. 
Vì chúng ta cần các cặp nhận dạng làm đầu vào cho mạch nên chúng ta sẽ tạo các cặp nhận dạng này một cách riêng biệt: just generate_identity
Điều này sẽ tạo ra kết quả tương tự như sau:< /p> p>
    include "circomlib/ Circuits/poseidon .circom" ;
Mẫu băm Poseidon được sử dụng như sau:
    thành phần main {public [ Identity_commitment,  message]} = SignMessage();
Theo mặc định, tất cả đầu vào vào mạch của chúng tôi đều ở chế độ riêng tư. Với điều này, chúng tôi đánh dấu rõ ràng identity_commitment và tin nhắn là công khai. Điều này có nghĩa là chúng sẽ trở thành một phần của sản phẩm công. 
Với thông tin này, bạn phải có đủ kiến ​​thức để hoàn thành mạch example3.circom. Nếu vẫn chưa hiểu, bạn có thể tham khảo example3-solution.circom để biết mã hoàn chỉnh. 
Như trước đây, chúng ta phải xây dựng mạch và chạy giai đoạn 2 của quá trình thiết lập đáng tin cậy: 
    {
      "identity_secret": "21879[...]1709",
   ;     "identity_commitment": "48269[...]7915",
      "tin nhắn": "42"< br >    
Hãy thoải mái thay đổi cặp nhận dạng thành cặp nhận dạng mà bạn đã tạo bằng cách sử dụng just generate_identity đúng không . Rốt cuộc, bạn muốn giữ bí mật danh tính của mình cho riêng mình! 
Bạn có thể nhận thấy rằng tin nhắn chỉ là một số ("42") được trích dẫn dưới dạng một chuỗi. Thật không may, do cách các ràng buộc hoạt động về mặt toán học (sử dụng đại số tuyến tính và mạch số học_), chúng ta chỉ có thể sử dụng số chứ không phải chuỗi. Các phép toán duy nhất được mạch hỗ trợ bên trong là các phép toán số học cơ bản như phép cộng và phép nhân. [^37]
Bây giờ chúng ta có thể tạo và xác minh bằng chứng:
    ["48968[...]5499", "48269[...]7915", " 42"]
Điều này tương ứng với chữ ký, cam kết và tin nhắn. 
Hãy xem mọi thứ có thể trở nên sai lầm như thế nào nếu chúng ta không cẩn thận. [^38]
Đầu tiên, điều gì sẽ xảy ra nếu chúng ta thay đổi lời hứa nhận dạng thành một điều gì đó ngẫu nhiên trong input.json? Bạn sẽ nhận thấy rằng chúng tôi không thể tái tạo bằng chứng. Điều này là do chúng tôi cũng đang kiểm tra cam kết nhận dạng bên trong mạch. Việc giữ bí mật danh tính và mối quan hệ giữa các cam kết là rất quan trọng. 
Thứ hai, điều gì sẽ xảy ra nếu chúng ta không đưa thông báo vào đầu ra? Chúng tôi đã có được bằng chứng và nó đã được xác minh. Nhưng tin nhắn có thể là _bất cứ thứ gì_, vì vậy nó không thực sự chứng minh rằng bạn đã gửi một tin nhắn cụ thể. Tương tự, điều gì sẽ xảy ra nếu chúng ta không đưa cam kết về danh tính vào kết quả đầu ra của công chúng? Điều này có nghĩa là cam kết nhận dạng có thể là bất cứ thứ gì, vì vậy chúng ta thực sự không biết ai đã ký tin nhắn. 
Là một bài tập suy nghĩ, hãy xem xét điều gì sẽ xảy ra nếu chúng ta bỏ qua một trong hai ràng buộc chính sau: 
identity_commitment === IdentityHasher.out
chữ ký <== signatureHasher.out
< /ul>
Xin chúc mừng, bây giờ bạn đã biết cách lập trình mã hóa! [^39]
Bài tập
Ba thành phần của sơ đồ chữ ký số là gì? 
Mục đích của việc sử dụng "Hàm băm thân thiện với ZK" như Poseidon là gì? 
Cam kết là gì? Làm thế nào chúng ta có thể sử dụng chúng cho các sơ đồ chữ ký số? 
Tại sao chúng tôi đánh dấu các cam kết nhận dạng và thông báo là công khai? 
Tại sao chúng ta cần cam kết về danh tính và hạn chế về chữ ký? 
Mã: Hoàn thành example3 cho đến khi bạn tạo và xác minh bằng chứng. 
Bước tiếp theo
Với sơ đồ chữ ký số ở trên và một số kỹ thuật chúng ta đã thấy trong bài viết, bạn có khả năng thực hiện những gì đã được đề cập ở đầu bài viết Tất cả các công cụ dành cho Lược đồ chữ ký nhóm. [^40]
Mã Skeleton tồn tại trong example4. Bạn chỉ cần 5-10 dòng mã. Cú pháp mới duy nhất là vòng lặp for, hoạt động giống như trong hầu hết các ngôn ngữ khác. [^41]. 
Mạch này sẽ cho phép bạn:
Ký tin nhắn
 < p>Chứng minh bạn là một trong ba người (cam kết danh tính)
Nhưng không tiết lộ ai
 Bạn có thể coi nó như một câu đố. Thông tin chi tiết quan trọng về cơ bản tóm gọn lại ở một biểu thức số học. Nếu có thể, hãy cố gắng giải quyết nó trên giấy. Nếu gặp khó khăn, bạn có thể xem lại cách giải như trước. 
Cuối cùng, nếu bạn muốn có thêm thử thách, đây là một số phương pháp mở rộng: 
Cho phép trong nhóm Nhiều người như bạn muốn
Thực hiện một mạch mới tiết lộ để chứng minh rằng bạn đã ký một tin nhắn cụ thể
 
Triển khai một mạch từ chối mới để chứng minh rằng bạn không ký một tin nhắn cụ thể nào
Việc tạo một giao thức mã hóa như vậy bằng các công cụ cổ điển sẽ là một điều A công việc lớn đòi hỏi nhiều chuyên môn. [^42] Sử dụng ZKP, bạn có thể trở nên năng suất và nguy hiểm trong một buổi chiều, coi những vấn đề này như nhiệm vụ lập trình. Đây chỉ là phần nổi của tảng băng chìm về những gì chúng ta có thể làm. 
Bài tập
Sự khác biệt giữa chữ ký nhóm và chữ ký thông thường là gì? Làm thế nào chúng có thể được sử dụng? 
Câu hỏi
Những câu hỏi này là tùy chọn và đòi hỏi nhiều nỗ lực hơn. 
Tìm hiểu cách triển khai IsZero(). 
Mã: Hoàn thành sơ đồ chữ ký nhóm ở trên (xem example4). 
Mã: Mở rộng ví dụ về chữ ký nhóm ở trên: cho phép nhiều người hơn và triển khai các mạch tiết lộ và/hoặc từ chối. 
Bạn sẽ thiết kế hệ thống "ZK ID" như thế nào để chứng minh bạn trên 18 tuổi? Bạn có thể muốn chứng minh những tính chất nào khác? Ở cấp độ cao hơn, bạn sẽ thực hiện nó như thế nào và bạn thấy những thách thức gì? Nghiên cứu các giải pháp hiện có để hiểu rõ hơn cách chúng được thực hiện. 
Đối với các chuỗi khối công khai như Ethereum, Lớp 2 (L2) đôi khi được sử dụng để cho phép giao dịch nhanh hơn, rẻ hơn và nhiều giao dịch hơn. Ở cấp độ cao, bạn sẽ thiết kế L2 bằng ZKP như thế nào? Giải thích một số thách thức bạn nhìn thấy. Nghiên cứu các giải pháp hiện có để hiểu rõ hơn cách chúng được thực hiện. ## Kết luận
Trong phần giới thiệu hướng dẫn này, chúng ta đã làm quen với cách viết và sửa đổi các bằng chứng không có kiến ​​thức cơ bản (ZKP) từ đầu. Chúng tôi thiết lập môi trường lập trình của mình và viết một mạch cơ bản. Sau đó chúng tôi thiết lập niềm tin, tạo và xác minh bằng chứng. Chúng tôi đã xác định được một số vấn đề và cải thiện mạch điện, đảm bảo kiểm tra các thay đổi của mình. Sau đó, chúng tôi đã triển khai sơ đồ chữ ký số cơ bản bằng cách sử dụng hàm băm và lời hứa. 
Chúng tôi cũng đã học đủ kỹ năng và công cụ để có thể triển khai chữ ký nhóm, điều này khó đạt được nếu không có bằng chứng không có kiến ​​thức. 
Tôi hy vọng bạn có một mô hình tư duy tốt hơn về những gì liên quan đến việc viết các bằng chứng không có kiến ​​thức và hiểu rõ hơn về chu trình chỉnh sửa-chạy-gỡ lỗi trong thực tế. Điều này sẽ cung cấp nền tảng tốt cho bất kỳ chương trình chứng minh không có kiến ​​thức nào khác mà bạn có thể viết trong tương lai, bất kể bạn sử dụng công nghệ nào. 
Lời cảm ơn
Cảm ơn Hanno Cornelius, Marc Köhlbrugge, Michelle Lai, lenilsonjr và Chih-Cheng Liang vì đã đọc bản thảo và đưa ra phản hồi. 
Hình ảnh
Đại hội Bourbaki 1938 - Không xác định, phạm vi công cộng, qua Wikimedia[11]
Những chú ngựa vằn của Hartmann - J. Huber, CC BY-SA 2.0, qua Wikimedia [12] 
Nhện cửa bẫy - P.S. Foresman, Miền công cộng, qua [Wikimedia](https://commons.wikimedia.org/wiki /File:Trapdoor_(PSF\ "Wikimedia").png)
Kingsley Lockbox - P.S. Foresman, Public Domain, qua Wikimedia[ 13]
Tài liệu tham khảo
[1] Trình dịch AI: https://learnblockchain.cn/people/19584
< span style="font-size: 14px;">[2] Nhóm dịch: https://learnblockchain.cn/people/412
[3] learnblockchain.cn/article…: https://learnblockchain.cn/article/9178
[4] Giới thiệu thân thiện về kiến ​​thức không có gì: https://learnblockchain.cn/article/6184
[5] kho git: https://github.com/oskarth/zkintro-tutorial
< span style="font-size: 14px;">[6]kho git: https://github.com/oskarth/zkintro-tutorial
[7]Tại đây: https://docs.circom.io/getting-started/installation/
[8]zkrepl.dev: https://zkrepl. dev/
[9]Tài liệu chính thức: https ://docs.circom.io/circom-lingu/signals/
[10]Giới thiệu thân thiện về bằng chứng không có kiến ​​thức: https://learnblockchain.cn/article/6184
[11]Wikimedia: https://commons.wikimedia.org/wiki/File:Bourbaki_congress1938.png
[12]Wikimedia: https://commons. wikimedia .org/wiki/File:Hartmann_zebras_hobatereS.jpg
[ 13 ]Wikimedia: https://commons.wikimedia.org/wiki/File:Kingsley_lockbox.jpg
< span style="font-size: 14px;">[14]AI Translator: https://learnblockchain.cn/people/19584
[15]Tại đây: https://github.com/lbc-team/Pioneer/blob/master/translations/9178. md
[16]^2]:  Xem [ Các tài liệu của chủ nghĩa liên bang (Wikipedia): https://en.wikipedia.org/wiki/The_Federalist_Papers#Authorship
 [17]^3]:  Xem [Bourbaki (Wikipedia): https://en.wikipedia.org/wiki/Nicolas_Bourbaki#Membership 
[18]^8]:  Điều này cho phép viết Các ràng buộc khá đầy thách thức, như bạn có thể tưởng tượng. Để biết thêm chi tiết về các ràng buộc trong Circom, hãy xem [ https://docs.circom.io/circom-lingu/constraint-thế hệ/:https://docs.circom.io/circom-lingu/constraint -thế hệ/ 
[19]^12]:   có nghĩa là nó có thể được biểu diễn dưới dạng tổ hợp tuyến tính chỉ bằng phép cộng. Điều này tương đương với phép nhân sử dụng hằng số. Điều chính cần lưu ý là các ràng buộc tuyến tính đơn giản hơn các ràng buộc phi tuyến. Để biết thêm chi tiết, hãy xem [Tạo ràng buộc: https://docs.circom.io/circom-lingu/constraint-thế hệ/
[20] Mạch số học: https://docs.circom.io/background/background/#arithmetic- Circuits< /span>
[21]^13]:  Về mặt toán học, những gì chúng tôi đã làm là đảm bảo rằng phương trìnhAz * Bz = Cz được thiết lập, trong đóZ=(W,x,1). A,  B và C là ma trận, W là nhân chứng (đầu vào riêng tư),  x là đầu vào/đầu ra công khai. Mặc dù biết điều này rất hữu ích nhưng không cần thiết phải hiểu nó khi viết mạch. Để biết thêm chi tiết, hãy xem [Hệ thống ràng buộc xếp hạng-1: https://docs.circom.io/background/background/#rank-1-constraint-system< p style="text-align: left;">[22]^15]:  Như trong bài viết Giới thiệu thân thiện Như đã đề cập trong , có một podcast dành cho giáo dân hay về Buổi lễ do Zcash tổ chức vào năm 2016, bạn có thể xem [tại đây: https://radiolab.org/podcast/ceremony< p style="text-align: left;">[23]^17]:  Chúng tôi gọi đó là mô hình tin cậy 1 trong 1 N. Có nhiều mô hình niềm tin khác; mô hình mà bạn có thể quen thuộc nhất là nguyên tắc đa số, trong đó bạn tin tưởng đa số mọi người sẽ đưa ra quyết định đúng đắn. Về cơ bản đây là cách thức hoạt động của nền dân chủ và bỏ phiếu theo đa số. [↩: #user-content-fnref-17
[24]^22]:  Còn được gọi là _giả thuyết về độ khó của mật mã_. Xem [Giả định độ cứng tính toán (Wikipedia): https://en.wikipedia.org/wiki/Computational_hardness_assumption#Common_cryptographic_hardness_assumptions
[25]^23]:  Để biết thêm thông tin, hãy xem [https://en.wikipedia.org/wiki/Integer_factorization: https:/ /en.wikipedia.org/wiki/Integer_factorization
[26 ]^24]:  Mặc dù chúng ta có thể thêm _asserts_, nhưng đây thực tế không phải là những ràng buộc và chỉ được sử dụng để làm sạch dữ liệu đầu vào. Để biết cách thức hoạt động của tính năng này, hãy xem [https://docs.circom.io/circom-lingu/code-quality/code-assertion/:https://docs.circom.io/circom-lingu/code-quality /code-assertion/
[27]https:// / www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions: https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions
[28]^25]:  Tài nguyên này được cung cấp bởi 0xPARC rất tuyệt vời nếu bạn muốn. để tìm hiểu thêm về nghệ thuật viết mạch (Circom): [https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/:https://learn.0xparc. org/materials/circom/learning-group-1/circom-1/
[29]^26]:  Do tính chất hạn chế khi viết nên tình trạng này xảy ra thường xuyên. Xem văn bản [https://en.wikipedia.org/wiki/Truth_table: https://en.wikipedia.org/wiki/Truth_table
[30]^27]:  Để biết thêm thông tin về circomlib, hãy xem [https://github.com/iden3/ circomlib: < em>https://github.com/iden3/circomlib
[31]^28]:  Xem [https://github.com/iden3/circomlib/blob/master/ Circuits/comparators.circom: https://github.com/iden3 /circomlib/blob /master/ Circuits/comparators.circom
 [32]^ 29]:  Mọi người thường chia sẻ những thứ này giữa các dự ánptau để cải thiện tính bảo mật. Để biết thêm thông tin, hãy xem [https://github.com/privacy-scaling-explorations/perpetualpowersoftau: https://github.com/privacy-scaling-explorations/perpetualpowersoftau< / p>
[33]https://github.com/iden3/snarkjs: https:// github.com/iden3/snarkjs
[34]^ 30 ]:  Cái thang ở đây đại diện cho một loại giá trị nào đó cho phép chúng ta tiến hành theo cách "cứng" ngược lại. Một cách khác để nghĩ về nó là một ổ khóa. Bạn có thể khóa nó dễ dàng, nhưng thật khó để mở khóa trừ khi bạn có chìa khóa. Hàm cửa bẫy cũng có định nghĩa chính thức hơn, xem [https://en.wikipedia.org/wiki/Trapdoor_function: https://en.wikipedia.org/wiki/Trapdoor_function
[35]^31]:  Ảnh chụp màn hình từ Wikipedia. Xem [ECDSA (Wikipedia): https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Signature_verification_algorithm
 [36]^38]:  Trong sơ đồ chữ ký số trong thế giới thực, khi nhiều tin nhắn được trao đổi, chúng tôi cũng có thể muốn giới thiệu một số ngẫu nhiên được mã hóa. Điều này nhằm tránh các cuộc tấn công lặp lại, trong đó ai đó có thể sử dụng lại chữ ký tương tự sau đó. Xem văn bản [https://en.wikipedia.org/wiki/Replay_Attack: https://en.wikipedia.org/wiki/Replay_Attack
[37]^40]:  Việc triển khai chữ ký nhóm trong ZKP được lấy cảm hứng từ 0xPARC, vui lòng xem [https://0xparc. org/blog/zk-group-sigs: https://0xparc.org/blog/zk-group-sigs
[38]^41]:  Xem [https://docs.circom.io/circom-lingu/control-flow/:  https ://docs.circom.io/circom-lingu/control-flow/
[39]^42]:  Ngược lại, các giấy tờ thực hiện chữ ký nhóm như [https://eprint.iacr.org/2015/043.pdf: https://eprint.iacr .org/2015/043.pdf