来源:Starknet 中文
引言
本文中间三段(如下)解释 Circle STARK 数学原理及公式,未翻译,详情请阅读原文:
STARK 效率意味着小数字
效率意味着优化乘法结构
走出思维定势(域)
Circle STARK 和 Stwo 为什么令人振奋?
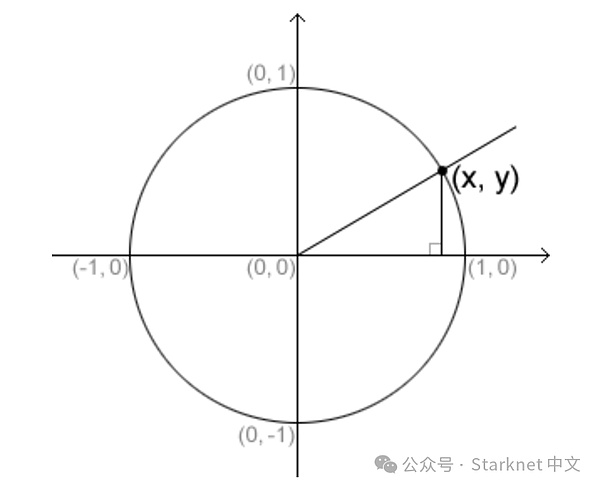
自以太坊推出 STARK 以来,上个月发表的研究成果是最令人兴奋的扩容技术突破之一。这项研究的数学原理很复杂,但使用了经典的圆形 circle(见图 1),将 STARK 的证明能力提高了 100 倍甚至更多。
该研究是由 Polygon Labs 的 Ulrich Haböck 以及 StarkWare 的 David Levit 和 Shahar Papini 合作完成,并将被广泛应用。StarkWare 也很荣幸能通过构建和开源 Stwo 证明器,迅速将其投入实际应用。在本文中,我将尽我所能地以最简单的方式来解释其中的数学原理及其重要性。
STARK 的可扩展性与透明性
我在 2017 年的斯坦福区块链会议上首次介绍了 STARK 一词。STARK 定义了一套确保计算完整性的协议,特别强调了可扩展性和透明性 — 分别对应 STARK 中的 S 和 T。可扩展性包括快速、低成本地生成和验证计算完整性证明,使公共使用无需依赖大量或昂贵的流程。这一特性对于在不同实体间应用完整性检查至关重要,并推动了 StarkWare 在区块链计算方面的改进。
STARK 的透明性意味着消除「可信设置」;所有程序都基于公开随机性,从而减少了信任假设。这对于维护计算的完整性至关重要,尤其针对那些可能利用系统参数的有影响力的实体。
可扩展性和透明性共同定义了 STARK 技术的核心,提供了安全、可扩展、透明且公开的验证方法。确保证明系统遵循这些原则对于维持有效、可靠的运行至关重要。无论你称呼你的系统为 STARK 还是其他名称,都请留意「可扩展性」和「透明性」双管齐下带来的显著优势,并询问你的本地证明提供者,其证明系统是否同时具备这两个特性。
从 Circle STARK 到 Stwo?
Stwo(即 STARK Two)是 Starknet 新一代证明器,旨在增强、加速,并最终取代当前的证明器 — Stone(即 STARK One)。Stwo 的效率预计将是 Stone 的 100 倍,将会使用基于 M31 的 Circle STARK 技术(如上所述)以及更多其他技术。其他的创新还包括 log-up 和总求和检查协议(如 Haböck 和 Papini 的最新研究成果)、同时处理多个不同次数的多项式(「混合次数」)以及用于编码电路和虚拟机的新基础设施。因此,除了预期 STARK 证明规模将提升至 Stone 的 100 倍之外,我们还能期待 Stwo 带来的更多其他优势,如更灵活地采用新编译器和虚拟机,从而提高开发速度。点击了解有关 Stwo 的更多信息。
网络成本大幅降低的计划蓝图涉及降低交易费用的机制,其中部分机制将立即生效。该计划包含多个步骤,其中部分步骤正同步推进中,将从多个方面解决交易费用昂贵的问题。
KZG 承诺与基于配对的 SNARK?
KZG 承诺是 Stone、Stwo 以及其他 STARK 使用的 FRI 协议的主要竞争对手,也是许多基于配对的 SNARK 的数学基础。其主要优势在于最终证明的极致简洁性,仅需要约 200 字节(而 FRI 和当前的 STARK 则需要好千字节)。其另一个优势是,通过针对特定 KZG 参数设置的预编译形式,在以太坊上获得优化支持,并通过 DankSharding 集成到核心以太坊协议中。这些优化支持解释了为什么许多 STARK 系统(如 Polygon、RiscZero 和 ZKsync 所使用的)最终会被封装在一个 SNARK 内部 — 目的是为了利用以太坊特定的预编译优化支持。只要对某些证明系统存在特定的优化支持,团队就会考虑将他们的 STARK 封装在 SNARK 内部,可以预期会有更多类似的情况发生。但是,与 KZG 安全素数相比(当前最佳实践要求这种素数超过 380 字节!),M31 的乘法运算速度要比其快 100 倍甚至更多,因此 KZG 和基于配对的系统在规模和吞吐量方面不太可能像 Stwo 那样高效。虽然椭圆曲线数学领域和基于配对的 SNARK 的创新范围之美令人叹为观止,但我们应该记住,这种 SNARK 不仅效率低下,而且需要可信设置,容易受到量子计算机的攻击。换句话说,就效率、安全性以及对未来的适应性方面,基于小型有限域的 STARK 是更好的选择。
最后的一些感想
Circle STARK 标志着 STARK 技术领域取得了激动人心的进步,已从理论走向实践。Circle STARK 也是日益复杂的 STARK 证明不断发展的最新里程碑。随着我们向前发展,这些证明将面临新的挑战,并将开启我们所未曾设想的应用领域。
看到深奥且魅力十足的数学被应用于系统中,为区块链的扩容带来指数级的增长,真是令人感到格外兴奋。区块链领域中的 ZK 技术不止一次地采用了前沿的「月亮数学」,并以此打造出创新产品。例如,Zcash 部署了首个为通用电路部署的 ZK-SNARK 系统,可在区块链上提供金融隐私;STARK 是以太坊上第一种最高效的未来证明扩容技术;Cairo 是用于编写可证明代码的新一代智能合约语言。因此,对于见证 Circle STARK 和 Stwo 还将解锁出哪些超出预期的奇妙应用和新颖数学,我感到非常期待!
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Bernice
Bernice Huang Bo
Huang Bo Cheng Yuan
Cheng Yuan Clement
Clement Bitcoinist
Bitcoinist Ftftx
Ftftx