إثبات الأصول على أساس ZK

الخلاصة

نحتفظ عمومًا بالعملات المشفرة وغالبًا ما نقوم بشراء وبيع وتبادل العملات في البورصات المركزية. تعتبر المعاملات في البورصات المركزية مريحة وسريعة للغاية، ففي أكثر من عشر سنوات منذ إصدار عملة البيتكوين، ظهرت العديد من البورصات المركزية في السوق، مما يسهل بشكل كبير عمليات شراء وبيع العملات المشفرة للمستخدمين. ومع ذلك، مع ازدهار البورصات المركزية، أصبح الاحتيال والسلوك الخبيث مثل سحب الأموال والهرب أمرًا شائعًا. قامت Netflix بتصوير فيديو ترويجي خصيصًا حول الانهيار المفاجئ للبورصة والوفاة الغامضة لمؤسسها: لا تثق بأحد، لغز العملة الافتراضية ^[1]. على وجه الخصوص، صدم إعلان إفلاس FTX بسبب الإعسار في عام 2022 العالم، وتكبد العديد من المستخدمين وشركات التمويل خسائر فادحة.

في الواقع، ليس فقط في مجال العملات المشفرة، ولكن أيضًا في المجالات التقليدية الأخرى، هناك عدد لا يحصى من السلوكيات التي تخدع المستثمرين من خلال الاحتيال المحاسبي. مثل حادثة إنرون التي صدمت العالم في بداية القرن الحادي والعشرين. اختيرت إنرون "الشركة الأمريكية الأكثر ابتكارا" من قبل مجلة فورتشن لمدة ست سنوات متتالية، إلا أن هذه الشركة التي تمتلك مئات المليارات من الأصول أفلست في غضون أسابيع قليلة في عام 2002. ومثال آخر هو شركة إيفرجراند، التي حولت الأموال المستخدمة في الأصل لبناء المباني لأغراض أخرى. وفي نهاية المطاف، كان عدد لا يحصى من أصحاب المنازل مثقلين بقروض الرهن العقاري لمدة ثلاثين عاما وانتظروا حتى يتم بناء المساكن غير المكتملة.

أحد الأسباب المهمة وراء عمليات الاحتيال التي لا نهاية لها في العديد من المجالات المختلفة هو أن أعمال التدقيق والمحاسبة في حد ذاتها ليست مفتوحة وشفافة تمامًا، مما يخلق مجالًا كبيرًا للفساد والفساد. الغش. . ومع ذلك، من أجل حماية مصالح الشركة وخصوصية المستثمرين، لا يمكن أن تكون البيانات المالية الرئيسية مفتوحة وشفافة تمامًا. لذلك، لم يكن هناك حل جيد للاحتيال المالي باستثناء تعزيز الرقابة. ومع ذلك، مع نضوج تقنية إثبات المعرفة الصفرية تدريجيًا، فإننا يمكن أن نرى ذلك إلى حل جديد.

إذا كان بإمكان كل مستخدم التحقق مما إذا كانت بعض أصوله بها احتيال مالي، فطالما كان هناك عدد كافٍ من المستخدمين الذين تم التحقق منهم، فإن المؤسسة تريد القيام بالاحتيال المالي سيكون صعبا للغاية. ولأن عملية التحقق هي عملية صفر معرفة، فحتى إذا اعترض الطرف الثالث البيانات أثناء نقل بيانات التحقق عبر الشبكة، فإنه لا يعرف ما هي الأصول الحقيقية للمستخدم، وبهذه الطريقة يمكن تنفيذ عملية التحقق بشكل كامل في الشبكة معروضة للعامة على الإنترنت. وبمساعدة تقنية إثبات المعرفة الصفرية، لم يعد قدر كبير من أعمال التدقيق خاضعًا لبراءة اختراع لبعض المنظمات مثل شركات المحاسبة الأربع الكبرى، ويتم إجراؤها سرًا خلف أبواب مغلقة. بل هي عملية مفتوحة يمكن لأي صاحب مصلحة أن يشارك فيها.

Summa^[2] هو مشروع بحث PSE يهدف إلى استخدام طريقة zk للتحقق من أصول المستخدم. سيقدم المحتوى التالي لهذه المقالة بإيجاز المشروع ومبادئ التنفيذ الفني.

العقد

يظهر الشكل إجمالي تدفق البيانات لـ Summa. تُستخدم العقود الذكية بشكل أساسي هنا لتخزين بعض البيانات العامة والتحقق منها. ليس بالضرورة أن يكون مرتبطًا بقوة بـ Ethereum، حتى لو تم نشره على سلاسل كتل أخرى مثل Solana في المستقبل (طالما أن Halo2 لديه دعم blockchain مطابق، يتم إنشاء بعض العقود في هذا المشروع بواسطة دليل Halo2^{[3 ]< /سوب>).}

يمثل الوصي الموجود في الصورة بورصة مركزية. يتم نشر العقد على السلسلة بواسطة البورصة، وملكية العقد مملوكة للبورصة، ولا يمكن تقديم البيانات العامة إلا عن طريق البورصة. تتكون البيانات العامة من جزأين، الجزء الأول هو المعلومات الأساسية للسلسلة التي يتم التحكم فيها عن طريق التبادل والتوقيعات الرقمية.

p>

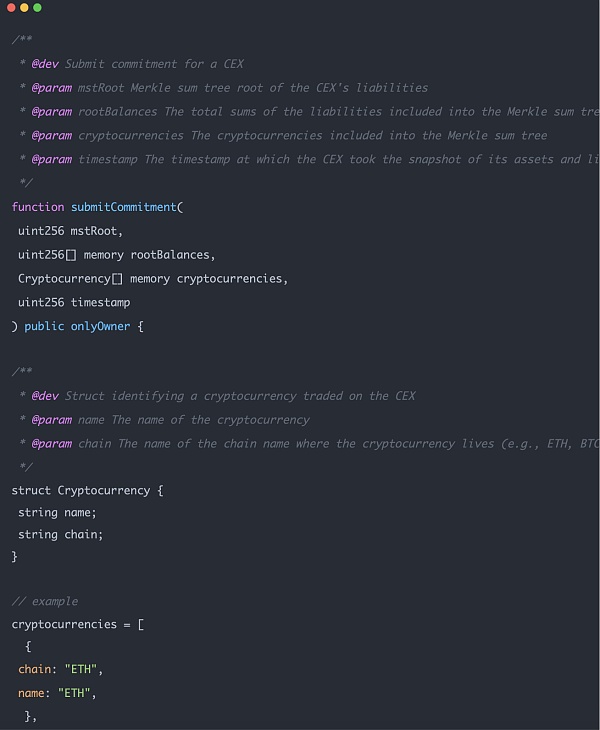
الجزء الثاني هو معلومات الأصول الموجودة في السلسلة، بما في ذلك التجزئة الجذرية لشجرة مجموع ميركل، والرصيد الجذري (العدد المحدد للأصول على السلسلة، مثل عدد BTC)، سيتم استخدام هذا الجزء من البيانات لإدخال مثيل إثبات zk.

p>

كلا الجزأين من البيانات متاحان بسهولة للعامة على السلسلة (باستثناء التجزئة الجذرية). سيكون من الصعب على البورصات الغش في هذه البيانات. يمكن لأي شخص مقارنة البيانات المخزنة في العقد مع نتائج البيانات الفعلية على عنوان blockchain.

يتم إنشاء إثبات حاليًا بواسطة التبادل. يرسل المستخدم المعلومات الأساسية التي يجب التحقق منها إلى التبادل، ثم يقوم التبادل بإنشاء الدليل وإعادته إلى المستخدم. يمكن للمستخدمين طلب العقد الذكي باستخدام هذا الإثبات، وسيقوم العقد بالتحقق من الإثبات.

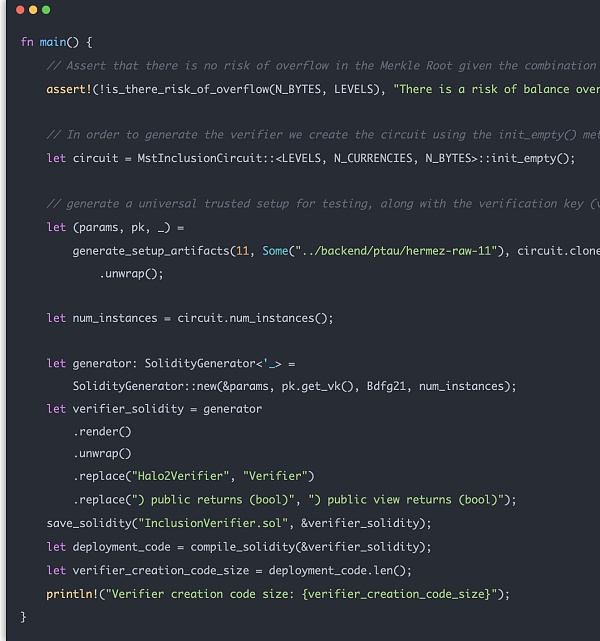
أخيرًا، إثبات التحقق هو المكان الذي يتفاعل فيه المستخدم مباشرة مع العقد. تتم ترجمة هذا الجزء من العقد إلى كود Solidity بواسطة دائرة Halo2 ثم يتم نشره على السلسلة كعقد تحقق منفصل.

p>

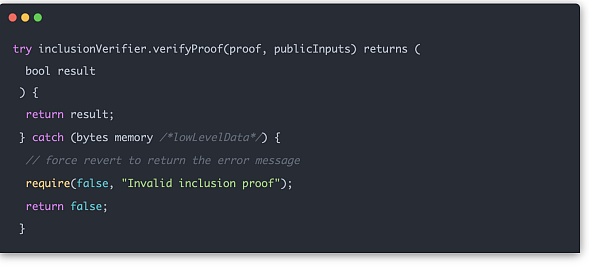
في الاستخدام الفعلي، يمكن تمرير الدليل لحساب السلسلة والتحقق منها.

p>

مثال التعليمات البرمجية التالي هو الوظيفة المستخدمة في عملية التجزئة الفعلية. يمكنك أن ترى أن حساب التجزئة بأكمله نفسه لا يستخدم عمليات البت، فقط الجمع والضرب الحسابات، والتي هي ZK ودية.

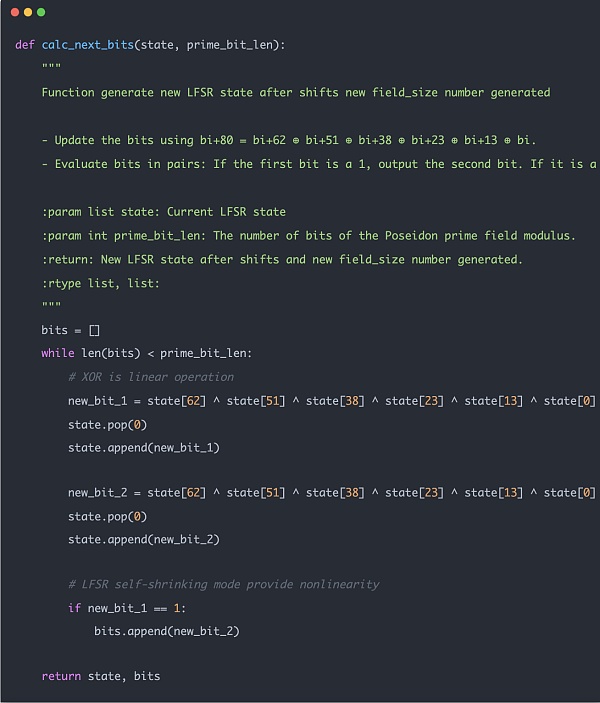p>

الفرق بين حساب بيانات zk وحساب البرنامج التقليدي هو أن بيانات zk يجب أن تُحسب في مجال محدود. عند إنشاء شجرة Merkle، تأكد من أن بيانات كل عقدة لا يمكن أن يتجاوز المجال المحدود، وهو أمر ضروري للغاية، ولهذا السبب، يجب التحقق من النطاق قبل الحساب حتى تفيض البيانات.

المبدأ العام لفحص النطاق مشابه للمثال أدناه. أولاً، بالنسبة لبيانات الإدخال، استخدم 8 بتات كوحدة طول واقطع نسخًا متعددة لتسهيل عمليات الطرح المستقبلية. ثم في كل مرة تقوم فيها بإجراء الحساب الرقمي التالي، اتبع خطوات الحساب في المثال أدناه. عندما تقوم دائرة التحقق من النطاق بإجراء قيود، فإنها تقوم في الواقع بإنشاء قيود بناءً على النتيجة المتوسطة diff = z_cur - z_next * Expression::Constant(Fp::from(1 << 8))، والتي يتطلب فرقًا طالما كان ضمن 8 أرقام. بهذه الطريقة، يتطلب قيد البيانات 32 بت فقط 4 خلايا حوسبة و256 جدول بحث، وفي المستقبل، سيكون قيد المثيل الذي يكون أعلى بت فيه 0 كافيًا. إذا لم يتم تصميمها بهذه الطريقة، فإن مجرد إجراء فحص لنطاق قيم 32 بت سيتطلب جدول بحث بحجمه، ومن الواضح أن مثل هذه الدائرة ستكون كبيرة جدًا ولا يمكن تطبيقها عمليًا.

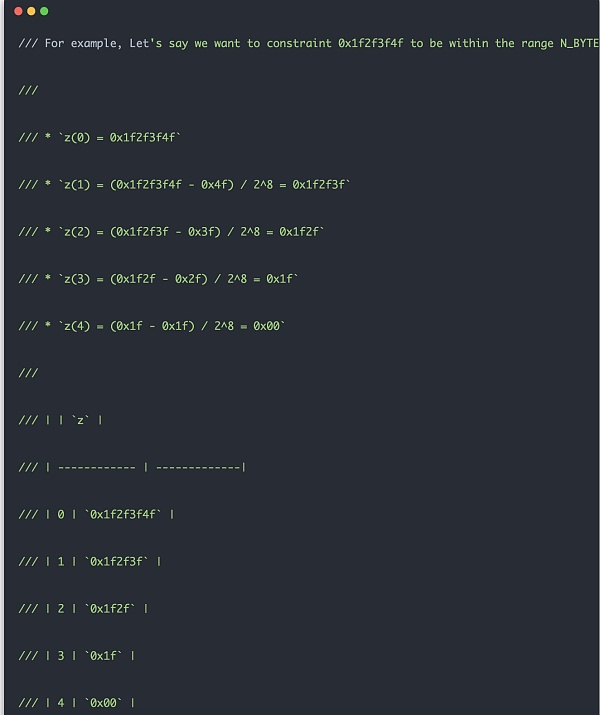p>

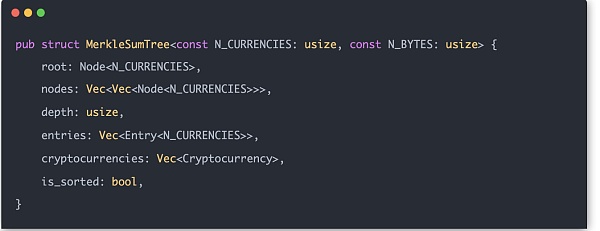
باستخدام هذه الهياكل المساعدة، يمكن إنشاء شجرة Merkle Sum Tree بشكل رسمي. تُسمى البيانات المدخلة لكل مستخدم باسم الإدخال، وبنيتها هي:

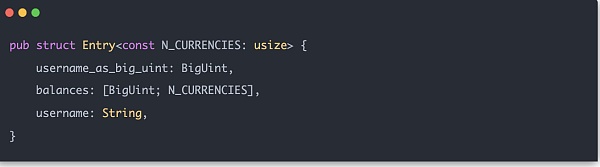
طريقة حساب التجزئة للعقدة الوسطى لشجرة Merkle هي H(LeftChild.balance[0) ] + RightChild.balance[0]، LeftChild.balance[1] + RightChild.balance[1]، ...، LeftChild.balance[N_CURRENCIES - 1] + RightChild.balance[N_CURRENCIES - 1]، LeftChild.hash، RightChild .hash)، وبالتالي فإن الطول الفعلي لمصفوفة vec المراد حسابها هو N_CURRENCIES + 2.

دعونا نبني شجرة Merkle بالكامل. جزء العقدة الطرفية بسيط نسبيًا، ما عليك سوى تحويل الإدخال إلى Node. يجب إنشاء العقد الوسيطة طبقة تلو الأخرى، وترتبط قيمة كل عقدة وسيطة بقيمة الشجرة الفرعية اليسرى والشجرة الفرعية اليمنى للطبقة التالية. أخيرًا، ضع نتائج العقدة الوسيطة المحسوبة في مصفوفة الشجرة:

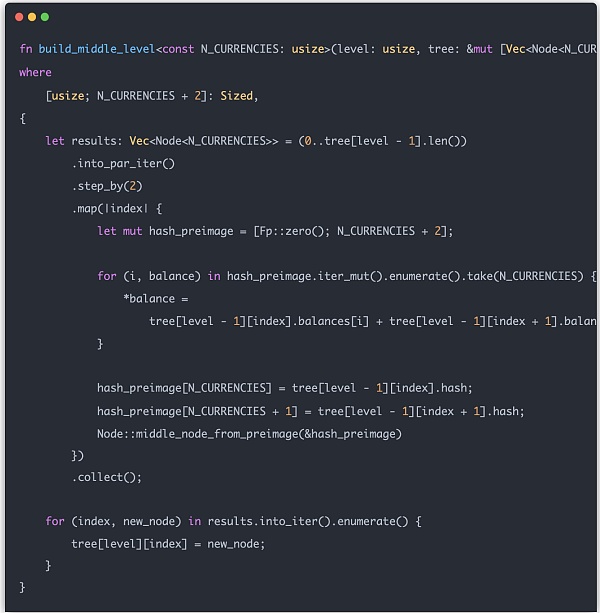
بعد ذلك نستخدم Merkle Tree لإنشاء دليل zk. ما يريد zk إثباته هو أن إدخال المستخدم موجود بالفعل في Merkle Tree. لذلك، نحتاج أولاً إلى صياغة فهرس إدخال محدد وإنشاء بنية البيانات المطلوبة لإثبات zk استنادًا إلى Merkle Tree.

p>

يمكننا تحقيق تأثير القيد بذكاء لجعل المعادلة بأكملها تساوي 0 عن طريق ضبط 0 و1.

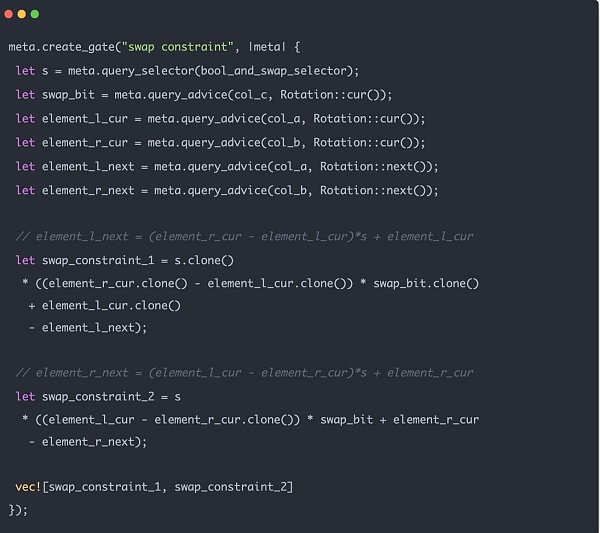
تتكون قيود Merkle Tree zk بشكل أساسي من جزأين. جزء واحد هو قيد المبادلة للتأكد من أنه عندما يقوم التبادل بإنشاء الدليل، فإنه يتم إنشاؤه بالفعل بالترتيب الحقيقي للشكل أعلاه. الجزء الآخر هو قيد التوازن، أي أن رصيد العقدة الأصلية يأتي من مجموع العقدة الفرعية اليسرى والعقدة الفرعية اليمنى. إن قيد مجموع الرصيد بسيط نسبيًا، ونحن هنا نركز على قيد المبادلة.

بنية بيانات شجرة Merkle zk sibling_middle_node_hash_preimages التي قدمناها من قبل عبارة عن مصفوفة ولا تحتوي على معلومات الموقع. سواء كان موضع المربع المنقط في الصورة يجب أن يكون على الجانب الأيسر أو الأيمن من الشجرة، فيجب الحكم عليه من خلال 0 و1 من path_indices. لذلك، يجب علينا التأكد من أنه عندما تكون القيمة 0، تكون العقدة الأم التي تم إنشاؤها على اليسار، والعقدة الشقيقة المقابلة لها من نفس المستوى على اليمين، وعندما تكون 1، فإن العكس هو الصحيح. عندما يتم استيراد البيانات إلى دائرة zk، يمكن تنفيذ هذا المنطق بسهولة في التعليمات البرمجية:

تتمثل عملية إثبات Merkle Sum Tree zk الشاملة في معالجة طبقة البيانات تلو الأخرى، ثم قم بتحويل فحص دائرة قيد zk لإدخال بيانات الموضع المقابلة. قم ببناء شجرة ميركل بأكملها. الناتج النهائي هو تجزئة العقدة الجذرية والرصيد الإجمالي، والذي يجب أن يكون متسقًا مع البيانات المقابلة في العقد. استخدم المثيل للتحقق من الاتساق. إذا كانت جميع عمليات التحقق صحيحة، فسيتم الانتهاء من عمل إثبات Merkle Tree بالكامل.

التحقق من الملاءة المالية

عملية إنشاء الدليل هي أن يطلب المستخدم التبادل و ثم يقوم المستخدم بعد ذلك بتداول بيانات الإثبات التي تم إرجاعها إلى العقد الذكي. في الوقت الحاضر، لا يدعم المشروع المستخدمين لتجاوز البورصة لإنشاء دليل بأنفسهم، لكنه يشعر أنه قد يكون اتجاهًا يمكن استكشافه في المستقبل. يتم إنشاء الأدلة مباشرة بواسطة المستخدمين بدلاً من إرجاعها بواسطة التبادلات. يمكن تجميع دائرة إثبات الهالة 2 بأكملها في تجميع الويب باستخدام الصدأ، ثم استخدام الإيثرات rs^[7] لإنشاء واجهة برمجة التطبيقات التفاعلية المقابلة. التعقيد الزمني للتحقق من جذر Merkle Tree هو السجل (n).قد لا يستغرق التحقق من جهاز المستخدم الكثير من الوقت، مما يعزز أمان اللامركزية.

المرجع

[1]

لا تثق بأحد، لغز العملة الافتراضية: https://www.netflix.com/hk/title/81349029

[2]

الخلاصة: https://github.com/summa-dev

[3]

تم إنشاء إثبات Halo2: https://github.com/privacy-scaling-explorations/halo2-solidity-verifier

[4]

تجزئة بوسيدون: https://github.com/ingonyama-zk/poseidon-hash

مرحلة إعداد المعلمة ومرحلة تشغيل التجزئة: https://autoparallel.github.io/ نظرة عامة/index.html

[6]

سجل إزاحة التغذية المرتدة الخطية: https: //en.wikipedia.org/wiki/Linear-feedback_shift_register

[7]

إيثرز آر إس: https://github.com/gakonst/ethers-rs

القراءة الموصى بها

سلسلة رؤى ZK

ملاحظات دراسة zkp

البودكاست الخاص بـ Wen Building

سلسلة المقالات التحليلية البحثية

سلسلة الترجمة الدقيقة Uniswap

Antalpha Labs  هو مجتمع مطوري Web3 غير ربحي مخصص لتعزيز الابتكار وتطبيق تكنولوجيا Web3 من خلال بدء ودعم البرامج مفتوحة المصدر.

الموقع الرسمي:https://labs.antalpha.com

تويتر:https://twitter.com/Antalpha_Labs

يوتيوب:https:/ / www.youtube.com/channel/UCNFowsoGM9OI2NcEP2EFgrw

اتصل بنا:[email protected]