原題:Adaptor Signatures and Its Application to Cross-Chain Atomic Swaps
元記事へのリンク:https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/
著者:mutourend, lynndell
1.はじめに
ビットコインのLayer2スケーリングスキームの急速な発展に伴い、ビットコインとそのLayer2相手との間のクロスチェーン資産移転の頻度が大幅に増加しています。送金の頻度が大幅に増加している。この傾向は、BitlayerのようなLayer2テクノロジーによって提供されるスケーラビリティの向上、取引手数料の低下、高いスループットによってもたらされている。これらの進歩は、より効率的で費用対効果の高いトランザクションを促進し、様々なアプリケーションにおけるビットコインの普及と統合を促進する。その結果、BitcoinとLayer2ネットワーク間の相互運用性は暗号通貨エコシステムの重要な構成要素になりつつあり、イノベーションを促進し、より多様で強力な金融ツールをユーザーに提供しています。
表1に示すように、BitcoinとLayer2間のクロスチェーン取引には3つの典型的なシナリオがあります。すなわち、集中型クロスチェーン取引、BitVMクロスチェーンブリッジ、クロスチェーンアトミックスワップです。これら3つの技術は、信頼の前提、セキュリティ、利便性、取引量の点で異なり、異なるアプリケーション要件を満たすことができます。
表1.クロスチェーン取引技術の比較
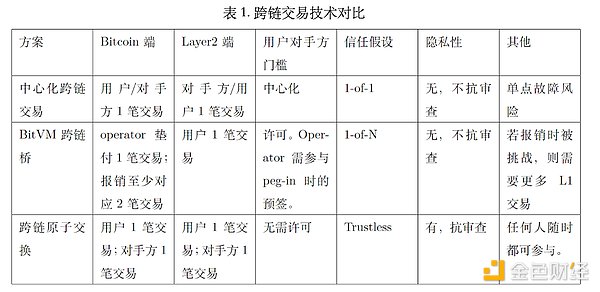
中央集権型クロスチェーン取引:ユーザーはまず中央集権組織(プロジェクトや取引所など)にビットコインを支払い、次に中央集権組織がL)で支払いを行い、次に中央の機関がLayer2ネットワーク上の資産の等価価値をユーザーが指定したアドレスに支払い、クロスチェーンでの資産移転が完了します。この手法の利点は、集中管理機関が迅速に取引の確認と処理を行えるため、スピードが速く、アグリゲーションプロセスが比較的容易であることである。しかし、この手法の安全性は、集中管理機関の信頼性と評判に完全に依存する。集中管理機関が技術的な障害、悪意のある攻撃、デフォルトに見舞われた場合、ユーザーの資金はより高いリスクにさらされる。さらに、中央集権的なクロスチェーン取引はユーザーのプライバシーを漏洩する可能性もあるため、ユーザーはこの方法を選択する際には慎重に検討する必要がある。したがって、その利便性と効率性はユーザーに大きな利便性を提供するものの、セキュリティと信頼が集中型クロスチェーン取引が直面する主な課題である。
BitVMクロスチェーンブリッジ:この技術は比較的複雑です。まず、ペグインフェーズで、ユーザーはビットコインのロックを実現するために、BitVMコンソーシアムが管理するマルチシグネチャアドレスにビットコインを支払います。対応する数のパスがレイヤー2で鋳造され、パスはレイヤー2のトランザクションやアプリケーションの実装に使用される。ユーザーが Layer2 パスを破棄すると、Operator がそれを繰り上げます。その後、Operatorは対応する数のビットコインをBitVMコンソーシアムが管理するマルチシグネチャプールに払い戻します。Operatorが悪意のある行為を行うのを防ぐため、払い戻しプロセスでは楽観的チャレンジメカニズムを採用しています。楽観的挑戦メカニズムを導入しているため、この技術は比較的複雑である。さらに、楽観的チャレンジ・メカニズムには、多数のチャレンジ・トランザクションとレスポンス・トランザクションが含まれ、トランザクション手数料は高い。その結果、BitVMクロスチェーンブリッジは、Uのインクリメンタル発行と同様に、超大規模なトランザクションにしか適用できず、したがって使用頻度も低い。
クロスチェーンのアトミックスワップ:アトミックスワップは、分散型の暗号通貨取引を可能にする契約です。この場合、「アトミック」とは、ある資産の所有権の変更は、実際には別の資産の所有権の変更を意味する。この概念は2013年にBitcointalkフォーラムでTierNolanによって初めて紹介され、4年間アトミックスワップは理論の領域にとどまっていた。DecredとLitecoinがアトミック交換に成功した最初のブロックチェーン・システムとなったのは2017年のことだった。アトミックスワップには2つの当事者が関与しなければならないが、第三者が交換プロセスを中断したり妨害したりすることはできない。つまり、この技術は非中央集権的で、検閲がなく、プライバシー保護に優れ、高頻度のクロスチェーン取引が可能で、分散型取引所での普及につながる。現在、クロスチェーン・アトミック取引所では4つのトランザクションが必要であり、いくつかのスキームではトランザクション数を2つに圧縮しようとしているが、取引当事者にとってリアルタイムのオンライン要件などが増えることになる。最後に、クロスチェーン原子交換技術は、主にハッシュタイムロックとアダプター署名を含んでいます。
ハッシュタイムロック(HTLC)ベースのクロスチェーン原子交換:クロスチェーン原子交換の実装に成功した最初のプロジェクトはDecredで、オンチェーンスクリプトの助けを借りて、ハッシュロックとタイムロックを利用しています。HTLCは、2人のユーザーが時間制限付きの暗号通貨取引を行うことを可能にするもので、受信者は指定された期間(ブロック数またはブロックの高さによって決定される)内に暗号証明("秘密")をコントラクトに提出しなければならず、さもなければ資金が交換される。")を提出しなければならず、そうでなければ資金は送金者に返却される。受信者が支払いを確認すれば、取引は成功する。したがって、参加する両方のブロックチェーンが「ハッシュロック」と「タイムロック」の機能を持つことが求められる。
HTLCのアトミック取引所は、分散型取引所技術における大きなブレークスルーを示していますが、問題もあります。これらのアトミック交換トランザクションとそれに関連するデータはオンチェーンで行われるため、ユーザーのプライバシー漏洩につながります。つまり、交換が行われるたびに同じハッシュ値が両方のブロックチェーンに現れ、わずか数ブロックしか離れていない。つまり、オブザーバーは交換に関与する通貨をリンクさせることができ、(タイムスタンプ的に)互いに近いブロックで同じハッシュ値を見つけることができます。チェーン全体で通貨を追跡する場合、ソースを特定するのは簡単です。この分析では、関連する身元データは明らかになりませんが、第三者は関係者の身元を簡単に推測することができます。
アダプターシグネチャーに基づくクロスチェーンのアトミックスワップ:BasicSwapが提供する2つ目のタイプのスワップは、「アダプターシグネチャー」アトミックスワップとして知られており、2020年にMonero開発者のJoël Guggerが発表した「バイナリーシグネチャー」という記事に基づいています。Monero開発者のJoël Gugger氏は2020年に「Bitcoin-Monero Cross-chain Atomic Swap}」と題する論文を発表した。この論文は、Lloyd Fournierの2019年の論文「One-Time Verifiably Encrypted Signatures, A.K.A. Adaptor Signatures」の実装と言える。アダプター署名は、秘密データを明らかにするために最初の署名と組み合わされる追加の署名であり、両当事者がデータの両方の部分を同時に互いに明らかにすることを可能にし、モネロのアトムスワップペアを可能にするスクリプトレスプロトコルの重要な構成要素です。
アダプター署名ベースのアトム交換には、HTLCアトム交換と比較して3つの利点があります。第1に、アダプター署名交換スキームは、時間ロックやハッシュロックなど、「シークレットハッシュ」交換が依存するオンチェーンスクリプティングを置き換えます。言い換えれば、HTLC交換における秘密と秘密ハッシュは、アダプタ署名交換にお いて直接対応するものはない。その結果、ビットコインの研究コミュニティでは「スクリプトレススクリプト」として知られている。さらに、そのようなスクリプトが関与しないため、チェーンのフットプリントが削減され、アダプタ署名ベースのアトミック交換が軽量かつ低コストとなります。最後に、HTLCでは各チェーンに同じハッシュ値を使用する必要がありますが、アダプター署名のアトミック取引所ではトランザクションをリンクすることができないため、プライバシーの保護が可能になります。
本稿ではまず、Schnorr/ECDSAアダプター署名とクロスチェーン原子交換の原理を紹介する。次に、アダプタ署名における乱数セキュリティ問題と、クロスチェーンシナリオにおけるシステム異種性とアルゴリズム異種性の問題を分析し、解決策を示す。最後に、アダプタ署名を拡張し、非インタラクティブなデジタル資産の保管を実現するために適用する。
2.アダプター署名とクロスチェーン原子交換
2.1シュナー・アダプター署名と原子交換

2.2ECDSAアダプター署名と原子交換

2.2.1 ゼロ知識証明 zk{v|Ṽ= v ᐧ G, V = v ᐧ Y}

3.セキュリティ上の問題と解決策
3.1 乱数の問題と解決策
3.1.1 乱数漏洩の問題
Schnorr/ECDSA アダプタ署名の事前署名はすべて、コミットメントȒに乱数 $r$ を作る。さらに、ゼロ知識証明は$Ṽ G,V = v ᐧ Y$を乱数$v$にコミットする。乱数が漏れると、秘密鍵が漏れることになる。
具体的には、Schnorrプロトコルでは、乱数$r$が漏洩した場合、式に従って使用することができます
$ŝ = r + c x.$
乱数$r$が漏洩した場合、式に従って使用することができます
乱数$r$が漏洩した場合、式に従って使用することができます。align: left;">秘密鍵$x$を計算する。
同様に、ECDSAプロトコルでは、乱数$r$が漏洩した場合、式に従って秘密鍵$x$を計算することが可能である
$ŝ = r^{-1}(hash(m)+R_x x)。$
$x$ から秘密鍵を計算する。
最後に、ゼロ知識証明プロトコルにおいて、乱数$v$が漏洩した場合、式に従って$x$から秘密鍵を計算することができる
$z := v + c r.$
乱数$r$を計算し、さらに乱数$r$に基づいて秘密鍵$x$を計算する。したがって、乱数は使用後すぐに削除する必要がある。
3.1.2乱数再利用問題
2つのクロスチェーントランザクションにおいて、同じ乱数がアダプター署名プロトコルで使用されると、秘密鍵の漏洩につながる可能性があります。具体的には、Schnorrプロトコルにおいて、同じ乱数$r$が使用された場合、$r$と$x$のみが以下の一連の方程式で未知となる
$ ŝ_1 =r + c_1 x, $
$ ŝ = r + c_2 x. $
このように、方程式系を解いて秘密鍵$x$を得ることができる。
同様に、ECDSAアダプタ署名プロトコルでは、同じ乱数$r$を使用する場合、$r$と$x$のみが以下の連立方程式で未知となる
$ ŝ_1 = r^{-1}(hash(m_1)+R_x x),$
$ ŝ_2 = r^{-1}(hash(m_2)+R_x x).
こうして、方程式系を解いて秘密鍵$x$を得ることができる。
最後に、ゼロ知識証明プロトコルにおいて、同じ乱数$v$を使用する場合、以下の連立方程式では$v$と$r$のみが未知となる
$z_1 = v+c_1 r, $
$ z_2 = v+c_2 r. $つまり、この連立方程式を解いて乱数$r$を求め、それをさらに解いて秘密鍵$x$を求めることができる。
類推すると、同じ乱数を使う別のユーザーも秘密鍵を漏らすことができる。言い換えれば、同じ乱数を使用する2人のユーザーが方程式系を解き、互いの秘密鍵を得ることができる。したがって、乱数の再利用問題を解決するには、RFC 6979を使用する必要があります。
3.1.3解決策:RFC 6979
RFC 6979は、DSAとECDSAを使用して決定論的電子署名を生成する方法を規定しており、kの乱数値を生成することに関連するセキュリティ問題に対処しています。セキュリティの問題を解決している。rfc 6979は、秘密鍵と署名されるメッセージから$k$を決定論的に導出する ことで、乱数を生成する必要性を排除している。これにより、同じメッセージに同じ秘密鍵を使って署名する場合、常に同じ署名になることが保証され、再現性と予測可能性が高まる。具体的には、決定論的な$k$はHMACによって生成される。このプロセスでは、ハッシュ関数(SHA256など)を使って秘密鍵、メッセージ、カウンターのハッシュ値を計算する
$k = SHA256(sk, msg, counter)。
上の式では、表現を簡単にするため、秘密鍵sk、メッセージmsg、カウンタcounterに対してのみハッシュを計算しています。この式は、kが各メッセージに対して一意であることを保証すると同時に、同一の 入力に対して再現可能であり、弱い乱数生成器や危殆化した乱数生成器に関連する、 秘密鍵が漏洩するリスクを低減する。このように、RFC 6979は、DSAとECDSAを使用した決定論的電子署名のための堅牢なフレームワークを提供し、乱数生成に関連する重大なセキュリティ問題に対処し、電子署名の信頼性と予測可能性を向上させる。Schnorr/ECDSA署名には乱数の欠陥があり、RFC 6979を使用してこれを防ぐ必要がある。したがって、Schnorr/ECDSAベースのアダプター署名もこれらの問題に悩まされており、また、これらの問題に対処するためにRFC 6979仕様を使用する必要があります。
3.2クロスチェーン・シナリオの問題と解決策
3.2.1UTXOとアカウント・モデリング・システムの異種問題と解決策
アダプター署名に基づくクロスチェーンのアトミックスワップ、少なくともECDSA曲線用に設計されたセミスクリプトレスアダプター署名スキームは、イーサとは互換性がありません。その理由は、Etherはアカウント・モデルであり、UTXOモデルではないからだ。具体的には、アダプタ署名ベースのアトミック交換では、払い戻しトランザクションに事前署名が必要である。しかしイーサネットシステムでは、nonceを知らずにトランザクショ ンに事前署名することはできない。その結果、ある当事者は事前署名の完了とトランザクションの実行の間にトランザクショ ンを送信することができる。これは事前署名されたトランザクションを無効にしてしまう(nonceはすでに使 用されており、再利用できないため)。
さらに、プライバシーの観点から、これはBitlayerスワップの匿名性がHTLCの匿名性よりも優れていることを意味します(スワップの双方が契約を見つけることができます)。しかし、一方の当事者が公開契約を持つ必要があるため、Bitlayer スワップはアダプター署名よりも匿名性が劣る。契約のない側では、スワップ取引は他の取引と同じように見える。しかし、EVM契約を結んでいる側では、その取引は明らかに資産スワップのためのものである。一方が公開契約を結んでいるにもかかわらず、高度なチェーン分析ツールを使っても、もう一方のチェーンまで追跡することは不可能である。
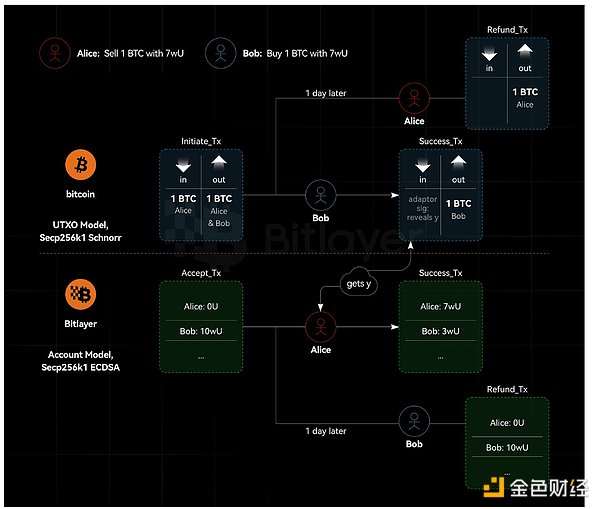
図1.UTXOとアカウントモデル化された異種システム間のクロスチェーン原子交換
。Bitlayerは現在ネイティブのECDSA署名をサポートしており、スマートコントラクトによるSchnorr署名検証も実装できる。Bitlayer ネイティブトランザクションが使用される場合、アトミック交換で払い戻しトランザクションに事前署名することはできません。アトミック交換を可能にするには Bitlayer スマートコントラクトトランザクションが必要です。しかし、このプロセスはプライバシーを犠牲にする。つまり、アトミック交換に関わるトランザクションはビットレイヤー・システムでは追跡可能だが、BTC システムのトランザクションには追跡できない。トルネードキャッシュのようなDappアプリケーションは、BTCとBitlayer間の原子交換のBitlayer側のトランザクションにプライバシーを提供するようにBitlayer側で設計することができる。
3.2.2同じ曲線、異なるアルゴリズム、アダプター署名セキュリティ
図2に示すように、ビットコインとビットレイヤーがともにSecp256k1曲線を使用していると仮定します。このケースは Schnorr と ECDSA アダプタ署名に基づいて証明可能な安全性がある。ECDSAとSchnorr署名述語が与えられたと仮定すると、ECDSAを破るシミュレータSを構築することが可能である。ECDSA署名述語のみが与えられたと仮定すると、ECDSAを破るシミュレータSを構築することが可能である。同様に、ECDSAとSchnorr署名述語機械があれば、Schnorr署名を破るシミュレータSを構築できると仮定すると、ECDSA署名述語機械だけがあれば、Schnorr署名を破るシミュレータSを構築できる。しかし、Schnorr署名は安全である。したがって、クロス・チェーン・シナリオでは、同じカーブを使用しても署名アルゴリズムが異なれば、アダプタ署名は安全である。言い換えれば、アダプター署名は、一方のエンドがECDSAを使用し、もう一方のエンドがシュナー署名を使用することを可能にする。
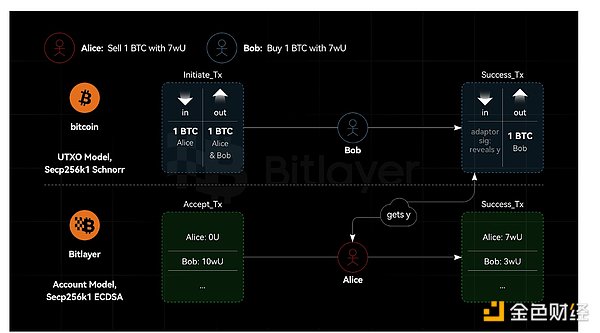
図2 同じ曲線、異なるアルゴリズム、アダプター署名
3.2.3 異なるカーブ、安全でないアダプタ署名
BitcoinがSecp256k1カーブとECDSA署名を使い、Bitlayerがed25519カーブとSchnorr署名を使うとします。この場合、アダプタ署名は使えない。bobは$y$をビットコインシステムのECDSA署名に適応させるとき、$s:= ŝ+y$を計算する。このとき、$y$の値空間はSecp256k1楕円曲線群のスカラー空間となる。その後、アリスは$y$を使ってed25519楕円曲線群のシュナー署名を行う必要がある。しかし、ed25519曲線の余弦は8であり、剰余係数はSecp256k1楕円曲線群の剰余係数と等しくない。したがって、ed25519曲線上のSchnorr署名に$y$を使うのは安全ではありません。
4.デジタル資産エスクローの応用
デジタル資産エスクローには、買い手アリス、売り手ボブ、カストディアンの3人の参加者がいます。アダプタ署名を使用することで、非対話的な閾値デジタル資産エスクローが可能になり、対話なしで閾値支出ポリシーのサブセットをインスタンス化することができます。このサブセットは、初期化に参加する者と参加しない者の2種類の参加者から構成され、後者をエスクロー・パーティと呼ぶ。カストロー・パーティは任意のトランザクションに署名することはできないが、サポートされているパーティの1つに秘密を送るだけである。
一方では、カストディアンはいくつかの固定された決済取引の中からしか選択できず、他の参加者の一人と新たな取引に署名することはできない。したがって、この秘密解除メカニズムにより、非対話型閾値エスクローは閾値シュナー署名よりも柔軟性が低くなる。一方、閾値シュナー署名を用いて2-of-3の支出ポリシーを設定することは可能である。しかし、閾値シュナー署名プロトコルは、分散型鍵生成プロトコルを実行するために3者間操作を必要とする。したがって、アダプター署名ベースの資産保管プロトコルは、非対話的な利点を持つ。
4.1アダプター署名に基づく非インタラクティブ資産保管
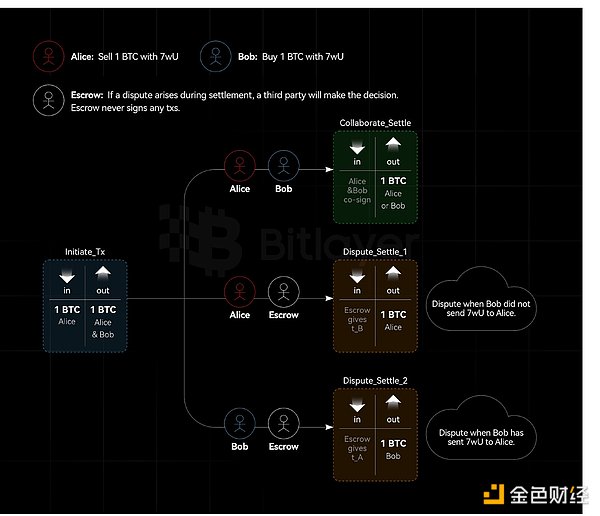
図3.資産エスクロー
図3に示すように、アリスとボブはエスクロー・パーティーを含む不可視の戦略で2対3のトランザクション出力を作成したい。条件$c$に応じて、アリスとボブのどちらかがこの取引出力を使うことができる。もしアリスとボブの間で争いがあれば、(公開鍵$E$と秘密鍵$e$を持つ)カストディ・パーティが、アリスとボブのどちらが資産を得るかを決定する。
BTCをアリスとボブの間の2-of-2のMuSig出力に送る、署名なしのFUNDINGトランザクションを作成します。li>
アリスはランダムな値$t_A$を選び、$t_A ᐧ G$の適応子を持つシュナー事前署名$( \hat{R}_A, \hat{s}_A)$ をあるトランザクションのためにボブに送る。Aliceは同時にBobに秘密$t_A$の組を含む暗号文を送り、エスクローされた公開鍵$E$を$E_c = E + hash(E, c)G$'s \textbf{verifiable encryption}$C = Enc(E_c, t_A)$に適合させる。BobがAliceの事前署名を受け取り、彼自身の署名を追加するプロセスは、2-of-2 MuSigを満たさないため、資金出力を使うことができない。資金出力は、Bobが$t_A$を知っている場合(これはカストディアンから提供される)、またはAliceがさらに完全な署名をしてBobに送る場合にのみ使うことができる。/li>
これに対応して、ボブは自分のアダプター秘密$t_B$に基づいてステップ(2)を繰り返す。
アリスとボブは受信した暗号文の正当性を検証し、暗号文が秘密$E_c$の暗号化であることを確認し、資金取引を署名してブロードキャストする。.検証可能な暗号化により、カストディアンをセットアップ段階に関与させる必要がなくなり、契約$c$を公開する必要がなくなる。
紛争があった場合、アリスとボブは暗号文と条件cをエスクロー・パーティに送ることができ、エスクロー・パーティは実際の状況を判断し、調整された秘密鍵$e+hash(E, c)$を使って$t_A/t_B$を復号し、ボブ/アリスに送ることができる。
公開された契約$c$は必要ない。
争いがない場合、アリスとボブは2-of-2のMuSig出力を好きなように使うことができます。
争いがある場合、当事者のどちらかがカストディアンに連絡し、その適応者秘密$t_Aまたは$t_B$を要求できる。その結果、当事者の一方は、カストディアン当事者の助けを借りて、そのアダプタ署名を完了し、その決済取引をブロードキャストすることができる。
4.2検証可能な暗号化
離散対数の実用的な検証可能な暗号化と復号化離散対数の実用的な検証可能な暗号化と復号化)は、特別に構造化されたグループの検証しかサポートしていないため、Secp256k1アダプタでは使用できません。
Purifyは元々、決定論的ノンス(DN)を持つMuSigプロトコルを作成するために提案されたもので、各署名者がゼロ知識を使用して、そのノンスが公開鍵とメッセージに擬似ランダム関数(PRF)を正しく適用した結果であることを証明する必要があります。ピュリファイPRFは、Secp256k1上の離散対数上で検証可能な暗号方式を作成するためのBulletproofsのゼロ知識プロトコルの演算回路に効率的に実装することができる。言い換えれば、検証可能な暗号化を実装するためにzkSnarkを使用します。
ジャグリング暗号化は次の4つのステップからなる:(1)離散対数$x$を$x = Γsum _k 2^{(k-1)l} x_k$となるような長さ$l$の複数の断片$x_k$にスライスする;(2)断片$x_k$に対して公開鍵$Y$を使用する。に対して公開鍵$Y$を用いてElGamal暗号化${ D_k, E_k} = \{ x_k ᐧ G + r_k ᐧ Y, r_k ᐧ G \}$; (3) 公開鍵$Y$を用いて各$x_kk ᐧ G$ $D_k$が$2^l$以下の値を持つPedersenコミットメント$x_k ᐧ G + r_k ᐧ Y$であることの範囲証明を作成する。sum D_k, sum E_k}$ が $x_k ᐧ G$ の正しい暗号化であることを証明せよ。
復号化処理では、各$x_k ᐧ G$を$Mc{D_k, E_k}$について復号化した後、(値が$[0, 2^l)$の範囲の)$x_k$を見つけるために網羅的探索を行う。
PurifyはBulletproofs内でPRFを実行する必要があり、これは比較的複雑であるが、Jugglingは理論的に単純である。また、証明サイズ、証明時間、検証時間における両者の差は非常に小さい。
5.まとめ
本稿では、Schnorr/ECDSAアダプター署名とクロスチェーン原子交換の原理を詳細に説明する。アダプタ署名は、乱数漏洩問題、重複問題に悩まされていることを深く分析し、これらの問題を解決するためにRFC6979の利用を提案する。さらに、クロスチェーンのアプリケーションシナリオを詳細に分析し、ブロックチェーンのUTXOモデルとアカウントモデルの違いを考慮するだけでなく、アダプタ署名が異なるアルゴリズムや異なるカーブをサポートするかどうかも検討する。最後に、アダプタ署名を拡張し、非インタラクティブなデジタル資産の保管を実現するために適用し、関係する暗号プリミティブである検証可能な暗号化について簡単に紹介する。
参考文献
Gugger J. Bitcoin-monero cross-chain atomic swap[J].chain atomic swap[J].
Fournier L. One-time verifiably encrypted signatures aka adaptor signature[J].signatures[J]. 2019, 2019.
https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf
Pornin T. Deterministic usage of the digital signature algorithm (DSA) and ellipticデジタル署名アルゴリズム(DSA)と楕円曲線デジタル署名アルゴリズム(ECDSA)[R]. 2013.
Komlo C, Goldberg I. FROST: flexible round-optimised Schnorr threshold signatures[C]//Selected暗号技術の分野:第27回国際会議、ハリファックス、ニューサウスウェールズ州、カナダ(仮想イベント)、2020年10月21-23日、改訂版選択論文27。International Publishing, 2021: 34-65.
https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md
https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/
カメニッシュJ、シュウプV.li>
Camenisch J. Shoup V. Practical Verifiable encryption and decryption of discrete logarithms[C]//Annual International Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003: 126-144.
Nick J, Ruffing T, Seurin Y, et al. MuSig-DN: Schnorr multi-signatures with verifiably deterministic non-conditions[C]//.
Slomovits O.Jugglingswap: scriptless atomic cross-chain swaps[J]. arXivプレプリントarXiv:2007.14423, 2020.
. Anais
Anais
 Anais
Anais Catherine
Catherine Kikyo
Kikyo Joy
Joy Catherine
Catherine Weatherly
Weatherly Kikyo
Kikyo Anais
Anais Catherine
Catherine Weatherly
Weatherly