著者:アーウィーヴ・オアシス、出典:PermaDAO
今回の記事は、論証の過程を数学的に導き出す部分が多く、少々硬派な内容になりますので、覚悟してください。しかし、基礎科目である数学は、物事を論理的に説明するのに非常に正確であると私は信じているので、@ArweaveEcoのメカニズムにおける数学の素晴らしさをわかりやすく示してみようと思う。
白書解釈(Ⅱ)の記事では、@ArweaveEcoの仕組みについて説明しています。)の記事では、データセットの特定の場所にあるデータを確かに保存したことを証明するために、どの参加者でもProof of Succinct Access(#SPoA)ゲームが使えることを説明した。このゲームでは、データセットのサイズに関係なく、データ転送と検証にかかるわずかなコストで、証明者が自分のデータのコピーを一定数保存していることを検証者に証明することができる。
SPoResゲーム
簡潔な複製証明(SPoRes)ゲームは次のようなものです。ボブはアリスが嘘をついていないことを確認したい。そのために、難易度パラメータdとランダムに生成されたシードをアリスに与え、アリスはそれを使って、1秒ごとにチェックポイントを生成するVDFハッシュチェーンを生成する。これらのチャレンジに対応するデータブロックがパックされるたびに、アリスは対応するSPoA証明を構築することができる。これらの証明はハッシュ化され、ボブの難易度パラメータdと比較される。もし証明のハッシュがdより大きければ、アリスは有効な解を見つけ、対応する証明をボブに送り、ボブはランダムシードを送ってからアリスの有効な証明を受け取るまでの時間を記録する。
難易度dに基づいて、1回の試行で有効な解を見つける確率pの式は次のようになります:
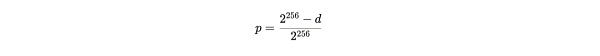
Formula note:SHA256ベースのアルゴリズムは256ビットの文字列なので、ハッシュの最大数は2^256(「^」は2乗を意味する)です。dより大きい有効解を見つけたい場合は、2^256-d個のハッシュしかなく、1回の試行で成功する確率を計算できます。
アリスにn個のレプリカがあり、1レプリカにつき1秒間にk回の試行ができる場合、与えられた秒数で解を見つけられる確率は次のようになります:

式の注釈: kNは、アリスが1秒間にできるハッシュ解の試行回数の合計を意味します。
上記の2つの式を導出に代入することで、次のようになります:
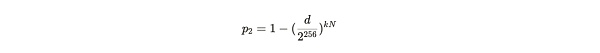
式の注釈: P2の式にpを代入して得られる結果
アリスが証明を提出するのに必要な時間は、幾何学的に次のように表すことができます。で表すことができる。この確率変数Xはd、k、nに依存する。アリスが嘘をついていることを検証するために、ボブはアリスが120秒ごとにボブに証明を提出できるような難易度dを送る。これはアリスの120秒間の成功確率が次のようになることに対応する:
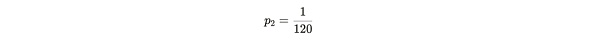
。式注: 1/120 は、120秒間に一度、証明の提出に成功する確率である
アリスが必要な時間内に証明を提出できるなら、彼女は正しい数のユニークなコピーを持っている可能性が高い。しかし、ボブがアリスが嘘をついていないと確信するには、1つの証明だけでは十分ではありません。もしアリスが長期間にわたって平均して120秒ごとに証明を提出し続けることができれば、ボブはアリスが望ましい量のデータを保存していると合理的に確信することができます。
次に、アリスのストレージに関するボブの確信度を定量化してみます。
アリスが20部保管し、2週間にわたって平均120秒の速度で一貫して証明を提出していると主張するとします(合計10,080の証明)。このときボブは、もしアリスが19部(またはそれ以下)しか保存していなかったとしたら、アリスがまだこれらの証明を提出できる確率はどれくらいだろうかと考える。
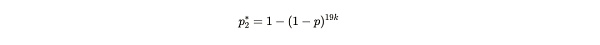
これは、別の秒に証明を提出する確率に相当します。方程式のメモ: ここに現れる19kは、アリスが19のコピーを保存し、各コピーが解を見つけるためにk回試行することを意味します。
単純化しすぎ:
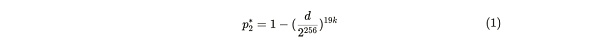
この確率は、ボブが正直なアリスのために生成するd値を使って計算することができます。もし彼女が19枚以下のコピーを保存していれば、彼女が1秒以内に証明を提供する確率は、以下に示す一連の導出によって求めることができる。ここでp2は、アリスが正直で20部保存している場合に、1秒間に証明を生成する確率を表し、p2*は、アリスが嘘をついている(保存部数≦19部)場合に、1秒間に証明を提供する確率を表す:
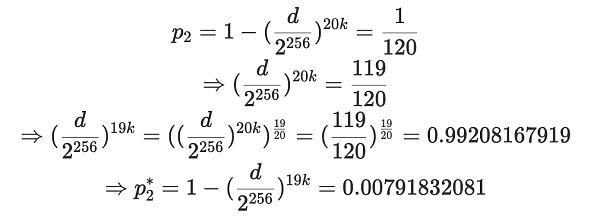
この導出は複雑に見えるかもしれないが、実は基本的な数学のスキルがあれば誰でも理解できる。その導出過程とは、前述の各社の置換過程である。
したがって、p2*=0.00791832081であり、これは126.2894秒の予想証明生成時間に相当する。アリスがp2*から得られる証明を提出する時間をX*とする。すなわち、X*~geom(p2*)である。これは、嘘の場合--19部しか保存されていない場合--にアリスが証明を提出するのに費やす時間X*の期待値(平均値)を表しています:
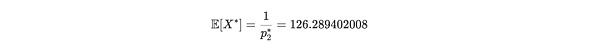
式注: E[X*]は、19部しか保存されていない場合にアリスが証明の提出に成功する平均時間が126.2894秒であることを意味します。もし彼女が20部保存していたら、提出に成功するまでの平均時間は120秒だったでしょう。
中心極限定理を使って、標本平均が120より低い、つまり上で得られた期待値E[X*]と異なる確率を見積もることができます。この確率は次のように表されます:
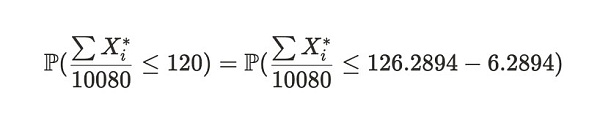
式の注意:式の左辺の式は、2週間の間に、アリスが毎回証明を提出するのに平均120秒以下かかる確率を表しています。式の右辺は左辺の式の変形である。
サンプルの数が多い場合、この不等式の左辺は平均E[X*]と分散σX*^2/nを持つ正規分布に収束する、ここでσX*はXdの標準偏差、n(ここでは=10,080)はサンプルサイズである。
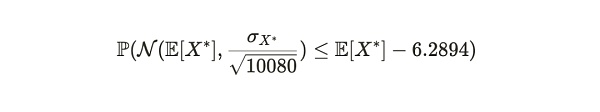
この分布を標準正規分布に変換して,等価確率を求めることができます。
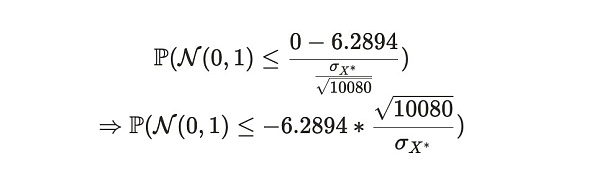
最後に、標準正規分布表を使って、アリスがこの1週間のタイムサイクルの間に嘘をつく確率を求めることができます:
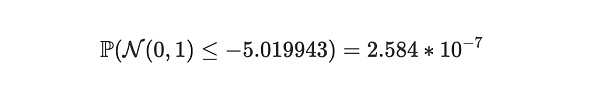
つまり、この例では、ボブは、アリスが2週間の間にデータセットのコピーを19個以上保存したことを、約99.99997416%の確度で決定することができます。もしアリスが19部未満しか保存していなければ、証明の提出時間は126.3秒以上になる。また、証明システム全体が120秒ごとに証明を送信する必要があるだけであることにも注意する。これは、アリスとボブ間の平均データ転送速度が2.389KB/秒(280KB/120秒)であり、ビットコインネットワークの同期オーバーヘッドに匹敵する。
最後に、これらの確率はデータセットのサイズを任意に増やしても変化せず、サンプリング期間を増やしても、アリスのコピー数に関するボブの確信の精度は超線形で向上し続けます(図1)。
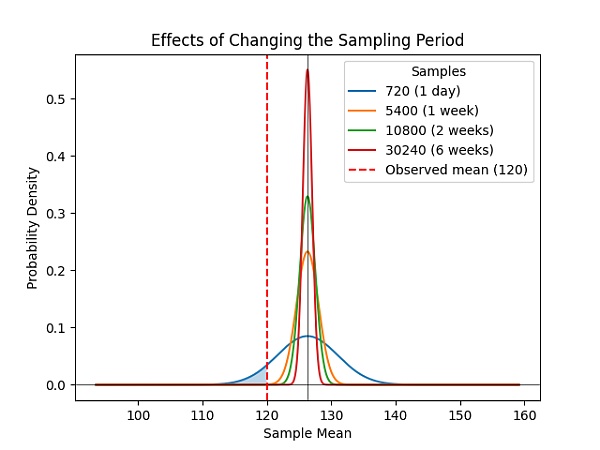
Figure 1: Determinism is super-linear relative to the increase in sample duration in the Proof of Succinct Replication (SPoRes) game.2週間のサンプル収集の後、19未満の複製を維持する確率は些細なものである(p<0.0000002584)。
つまり、SPoResゲームは以下のパラメータで定義されます。strong>r= ゲームに使用するデータセットのメルケル・ルート。
k=コピーごとに1秒間にアンロックされるチャレンジの最大数。
d= 各チャレンジの成功確率を決定する難易度パラメータ。
このような興味深い数学的導出により、妥当な期間にわたって採掘者に一貫して証明を提出させるだけで、データが保存されているかどうかを安全に判断することができます。これが、分散型ストレージを目指すArweaveのコンセンサス・メカニズムの中核を成す。数学的な楽しみはまだ始まったばかりであり、今後さらに興味深い推論や議論が展開される予定である。
引用リンク
1.アルウィーヴ・エコTwitter:
。https://twitter.com/@ArweaveEco
2. #SPoA:
https://
3.align: left;">https://twitter.com/search?q=%23SPoRes&src=hashtag_click
4.元記事へのリンク:
4.p>https://twitter.com/ArweaveOasis/status/1772089247660638417
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Others
Others Cointelegraph
Cointelegraph