著者: Vitalik Buterin、翻訳: Kurt Pan、XPTY
この記事は、SNARKとSTARKがどのように機能するかについての基本を理解していることを前提としています。Eli ben-Sasson氏、Shahar Papini氏、Avihu Levy氏、そしてフィードバックとディスカッションを提供してくれたstarkwareの他の方々に感謝します。

このシフトはすでに証明速度の劇的な向上をもたらしており、特にStarkwareはM3ラップトップで1秒間に62万個のPoseidon2ハッシュを証明する能力を持っています。具体的には、ハッシュ関数の一部としてPoseidon2を信頼する限り、効率的なZK-EVMを構築する最も困難な部分の1つが効率的に解決されたことを意味する。しかし、これらのテクニックはどのように機能するのだろうか?また、これらのドメイン上で暗号証明(セキュリティのためにしばしば大きな整数を必要とする)はどのように構築されるのだろうか?また、これらのプロトコルはBiniusのようなよりエキゾチックな構築と比較してどうなのだろうか?この投稿では、Circle STARKsと呼ばれる構成(Starkwareのstwo、Polygonのplonky3、そして私自身のpython実装で実装されている)に特に焦点を当てながら、これらのニュアンスのいくつかを探ります。
https://x.com/StarkWareLtd/status/1807776563188162562
https://vitalik.eth.limo/general/2022/08/04/zkevm.html
https://vitalik.eth.limo/general/2024/04/29/binius.html
https://www.irreducible.com/posts/binius-hardware-optimised-snark
https://eprint.iacr.org/2024/278
https://eprint.iacr.org/2024/278
https://github.com/starkware-libs/stwo
https://github.com/Plonky3/Plonky3
https://github.com/ethereum/research/tree/master/circlestark
小規模ドメインでよくある問題
ハッシュベースの実行時ハッシュベースの証明(あるいはあらゆるタイプの証明)を行う際の最も重要な「トリック」の1つは、ランダムな点の多項式について証明するのではなく、基礎となる多項式について証明することです。

https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic
この問題には2つの自然な解決策があります:
- multiple randomisation test
- https://www2.clarku.edu/faculty/djoyce/complex/mult.html

ここでの実装は最適ではありません。唐津葉で最適化できる)、原理を示しただけ



- https://eccc.weizmann.ac.il/report/2017/134/

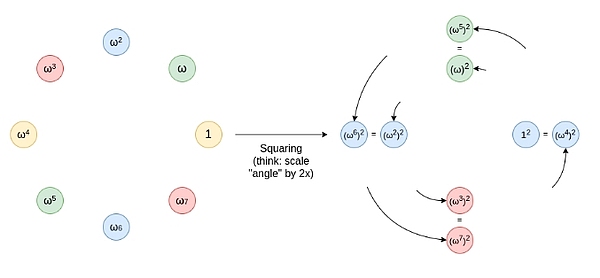

サークルFRI

- https://elibensasson.blog/why-im-excited-by-circle-stark-and-stwo/
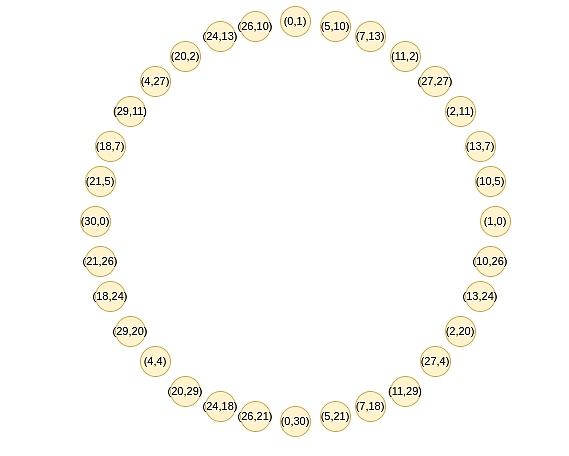
これらの点は足し算の法則に従っています。最近、三角法や複素数の掛け算を勉強した人には見覚えのある法則かもしれません:
- https://

< p style="text-align: center;">
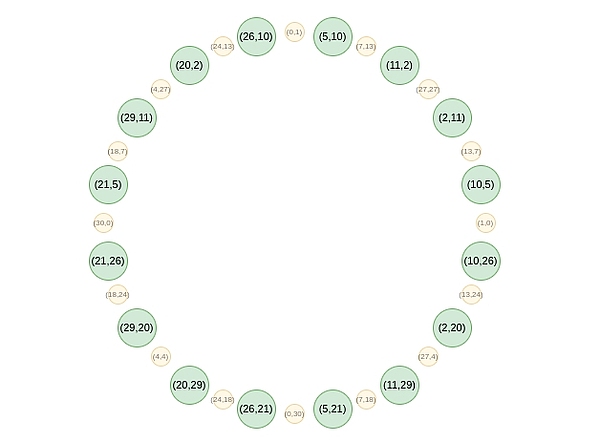
第2ラウンド以降、マッピングが変わります:

Circle FFT
- https:/?/vitalik.eth.limo/general/2019/05/12/fft.html


- https://www.researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_Finite_Fields
- .Finite_Fields
ここからは、通常のSTARKと比較してCIRCLE STARKを実装する人にとって異なる、より難解な詳細について説明します。
得点指数

- https://eprint.iacr.org/2019/336


Disappearing polynomial

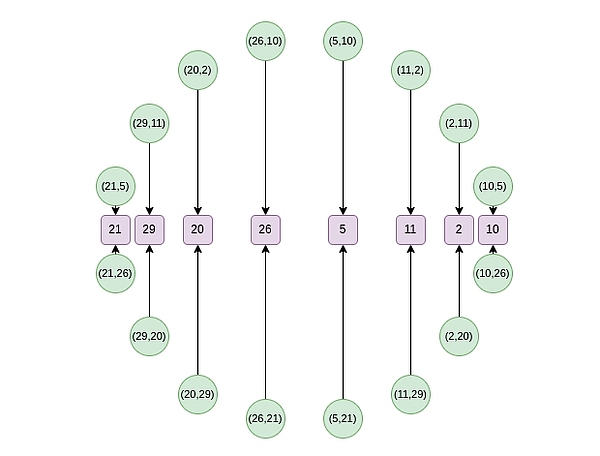
Reversing Bit Order

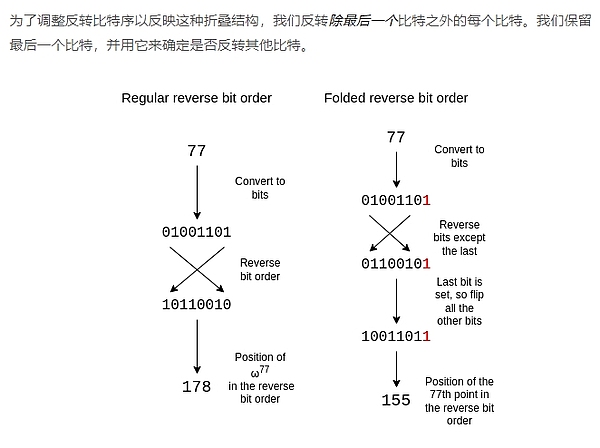

効率
で、円。また、ルックアップテーブルのオーバーヘッドなしに32ビット加算を実行するオプションも提供します。サークルSTARK(およびBabyBearベースの通常のSTARK)は概念的に非常にシンプルです。
結論:サークルSTARKについてどう思うか?
サークルSTARKは、通常のSTARKと比べて開発者にあまり追加の複雑さをもたらしません。サークル FRI が操作する「多項式」の背後にある数学は、かなり直感に反しており、理解して理解するのに時間がかかります。Circleの数学の複雑さはカプセル化されており、体系化されているわけではありませんが、開発者があまり見ないように隠されています。
https://vitalik.eth.limo/general/2022/02/28/complexity.html
https://vitalik.eth.limo/general/2022/02/28/complexity.html
円FRIと円FFTを理解することは、他の "エキゾチックなFFT "を理解するための良い知的方法でもあります。LibSTARKは、楕円曲線FFTのような、よりエキゾチックな構成と同様に、少数対一のマッピングを使用し、楕円曲線点演算とうまく機能します。
https://github.com/ethereum/research/blob/master/binius/binary_ntt.py#L60
https://github.com/elibensasson/libSTARK
https://arxiv.org/abs/2107.08473
Mersenne31、BabyBear、そしてBiniusのようなバイナリドメイン技術を組み合わせることで、私たちはSTARKの「ベースレイヤー」の限界に近づいていると感じています。"効率の限界に近づいていると感じています。現時点では、STARKの最適化のフロンティアは、ハッシュ関数や署名のようなプリミティブの最も効率的な演算化(およびこの目的のためのプリミティブ自体の最適化)、より多くの並列化を解除するための再帰的な構成、開発者のエクスペリエンスを向上させるためのVMの演算化、およびその他の上位層のタスクにシフトすると予想しています。
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Catherine
Catherine Beincrypto
Beincrypto Coindesk
Coindesk Bitcoinist
Bitcoinist 链向资讯
链向资讯 Ftftx
Ftftx Cointelegraph
Cointelegraph