비트코인의 힘의 법칙 이론
비트코인은 일반적인 자산이라기보다는 자연 현상에 가깝습니다. 비트코인은 금융 자산이라기보다는 하나의 도시이자 유기체와 비슷합니다.
 JinseFinance
JinseFinance
편집: 리우 티칭체인
티칭체인 참고: 본 글은 해롤드 크리스토퍼 버거와 피터 비인의 공동 논문 '비트코인의 시간 기반 힘의 법칙과 코인 통합 재조명'의 번역본입니다. 기반 파워 법칙과 코인 통합 재검토, 2024.1.31)를 번역한 것으로, 보다 이론적이며 통계학에 어느 정도 기초가 있는 독자에게 적합합니다. 기초가 부족한 독자들이 쉽게 이해할 수 있도록 먼저 간단한 설명을 덧붙입니다.
시간의 힘의 법칙 모델이라고 불리는 것은 지난 몇 년 동안 여러 기사에서 소개된 바 있습니다.
업계에서 잘 알려진 익명의 애널리스트 중 한 명인 PlanB는 S2F 경도를 사용하여 가격을 모델링하는 것을 적극 지지해 왔으며, 이를 S2F 모델이라고 합니다. 하지만 안타깝게도 S2F 모델은 잘못된 모델입니다. 하지만 그렇다고 해서 S2F 지표가 무의미하다는 의미는 아니며, 가격과 관련된 S2F 경도의 변화가 PlanB가 생각하는 것만큼 '급진적'이지 않다는 의미일 뿐이라는 점에 유의하시기 바랍니다.
다음 그래프는 파워 법칙 모델과 S2F 모델 간의 관계를 명확하게 보여줍니다.
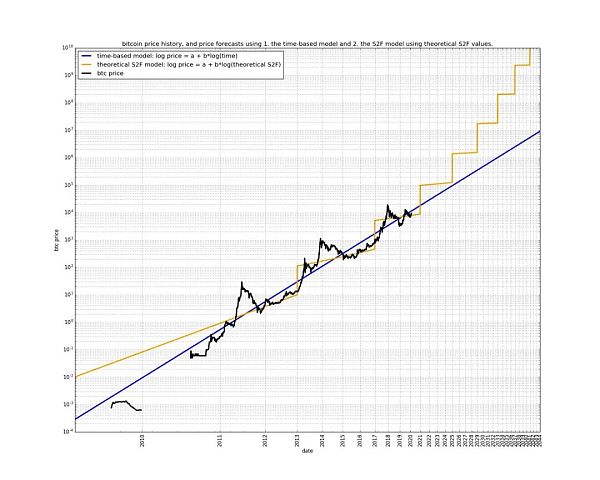
명백하게도, S2F 모델은 시간의 선형적 경과가 기하급수적인 가격 상승을 주도하는 것으로 보는 반면, 파워 법칙 모델은 시간의 선형적 경과가 기하급수적인 가격 상승을 주도하는 것으로 봅니다. 파워 법칙 모델은 기하급수적인 시간의 흐름이 기하급수적인 가격 상승을 주도한다고 간주합니다.
일반적으로 S2F 경도를 사용해 생산량 반감으로 인한 '위상 변화'를 시각화하지만, 파워 법칙 모델을 사용하면 비트코인을 이중로그 공간에서 선형 회귀로 변환할 수 있습니다. 파워 법칙 모델의 우아함에는 서포트 벡터 머신(SVM)의 느낌이 있어 제 취향에 딱 맞습니다.
H. Burger & P. Vijn.Enjoy!
* * *
비트코인의 시간 기반 전력 법칙은 원래 Giovanni 산토스타시가 2014년에 제안한 것을 2019년에 재구성한 것으로(회랑 또는 3변수 모델), 비트코인 가격과 시간 간의 관계를 설명합니다. 구체적으로 이 모델은 비트코인 생성 블록 이후 일수의 로그와 비트코인 USD 가격의 로그 사이의 선형 관계를 설명합니다.
이 모델은 마르셀 버거, 팀 스톨테, 닉 엠블로우 등 많은 비평가들의 관심을 끌었으며, 이들은 각각 이 모델에 대한 "반박문"을 작성했습니다. ". 이 글에서는 이 세 가지 비평의 핵심 주장 중 하나인 시간과 가격 사이에 공적분(동조화)이 없다는 주장, 즉 이 모형이 "유효하지 않으며" 단지 가짜 관계를 보여줄 뿐이라는 주장에 대해 분석해 보겠습니다.
이것이 정말 사실일까요?
이 백서에서는 이 질문에 대해 자세히 살펴봅니다. 그 결과, 엄밀히 말하자면 우리 모델을 포함한 시간 의존적 모델에서는 공분산이 존재할 수 없다는 결론을 내렸습니다. 그러나 공적분에 필요한 통계적 특성 중 하나가 시간 기반 전력법 모델에 존재한다는 것은 부인할 수 없는 사실입니다. 따라서 우리는 시간 기반 파워 법칙 모델이 좁은 의미에서 공적분이며, 우리의 비판은 잘못된 것이며, 이 모델은 완벽하게 유효하다는 결론을 내립니다. 이 결론은 "주식 증가율"(S2F) 모델과 장기 주식 시장 지수 가격에서 관찰되는 지수 성장에도 동일하게 적용됨을 보여줍니다.
길을 잃으셨나요? "코인 통합"이라는 용어가 익숙하지 않으신가요? 걱정하지 마세요. 인과 추론 및 비위성 관계 분야의 전문가이자 '왜'의 저자 유디아 펄은 이 주제에 대해 아무것도 모른다고 주장합니다. 당면한 용어를 완전히 명확히 하기 위해 노력하겠습니다.
트위터에서 비트코인 관련 토론에서 공분산에 대한 논쟁은 흥미롭고 상당히 흥미로웠습니다. "주식 증가율"과 "힘의 법칙"에 대해 많은 팔로워들이 혼란스러워하고 있습니다. 관심 있는 독자는 "동조화란 무엇인가"를 검색하여 직접 확인할 수 있습니다. 시간이 지남에 따라 일부 기여자들은 이해의 폭을 넓히고 다듬은 반면, 다른 기여자들은 여전히 혼란스러워하거나 편을 바꾸거나 길을 잃은 것처럼 보입니다. 이제야 우리는 이 주제에 집중하기 시작했습니다.
확률적 프로세스에는 무작위 변수가 포함됩니다. 무작위 변수의 값은 미리 정해져 있지 않습니다. 반면 결정론적 프로세스는 모든 측면이 미리 알려져 있기 때문에 사전에 정확하게 예측할 수 있습니다. 예를 들어 주식 시장 가격은 자산의 가격을 미리 예측할 수 없기 때문에 무작위 변수에 해당합니다. 따라서 우리는 주식이나 비트코인 가격과 같은 시계열을 무작위 변수에 대한 관찰로 취급합니다.
반면, 시간의 흐름은 결정론적 패턴을 따릅니다. 매초는 불확실성 없이 지나갑니다. 따라서 이벤트가 발생한 후의 시간은 결정론적 변수입니다.
동일성을 살펴보기 전에 동일성의 기본 개념인 고정성을 살펴봅시다:
그림 해석: 주황색 선을 한 번 차분하면 파란색 선이 나옵니다. I(1) 시계열을 한 번 차분하면 I(0) 시계열이 나옵니다.
평활 프로세스(고정 프로세스)는 넓은 의미에서 시간이 지나도 동일한 속성을 갖는 확률적 프로세스입니다. 예를 들어, 정지된 프로세스의 경우 평균과 분산이 결정되고 안정적입니다. 고정 시계열의 동의어는 I(0)입니다. 정지된 프로세스에서 시작된 시계열은 "드리프트"가 없어야 하며 평균(일반적으로 0)에 수렴해야 합니다.
비평활 과정의 예로는 물리학의 브라운 운동이나 입자 확산과 같은 랜덤 워크가 있습니다. 랜덤 워크에서 각각의 새로운 값은 이전 값에 난수를 더한 값에 따라 달라집니다. 비평활 과정의 속성(예: 평균 및 분산)은 시간에 따라 변하거나 정의되지 않습니다. 비평활 과정은 I(1) 이상이지만 일반적으로 I(1)입니다. 비고정형 프로세스에서 비롯된 시계열은 시간이 지남에 따라 "드리프트", 즉 고정된 값에서 벗어나는 경향이 있습니다.
I(1) 기호는 시계열이 안정성에 도달하기 위해 몇 번이나 "차분"해야 하는지를 나타냅니다. 차분은 시계열의 한 값과 이전 값 사이의 차이를 찾는 과정입니다. 이는 미분을 구하는 것과 비슷합니다. 고정 시계열은 이미 고정되어 있으므로 0번 미분해야만 고정이 되므로 I(0)이 됩니다. I(1) 시계열은 한 번 미분해야만 고정이 됩니다.
위 그래프는 주황색 시계열을 한 번 미분하여 파란색 시계열을 구하는 방식으로 그려져 있습니다. 마찬가지로 주황색 시계열은 파란색 시계열을 적분하여 얻을 수 있습니다.
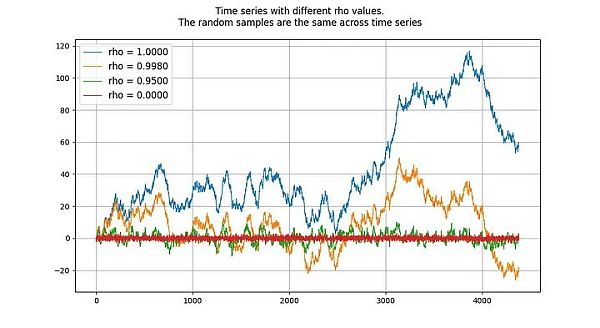
단위근 프로세스는 rho 매개변수가 1로 추정되는 자동 회귀 모델(더 정확하게는 AR(1) 유형)을 말합니다. rho와 root를 혼용하여 사용할 수 있지만, rho는 실제 값을 나타냅니다. 로와 루트를 같은 의미로 사용할 수 있지만, 로는 프로세스의 실제 값을 의미하며 일반적으로 알 수 없으므로 추정해야 합니다. 결과는 "루트" 값입니다.
rho의 값은 프로세스가 이전 값을 얼마나 잘 기억하는지를 나타냅니다. u는 백색 잡음으로 가정되는 오류 항을 나타냅니다.
이미지 src="https://img.jinse.cn/7198478_image3.png">
단위 루트 프로세스는 확률적 방황 프로세스로, 부드럽지 않습니다. "루트" 또는 rho 값이 1 미만인 프로세스는 드리프트하지 않는 경향이 있으므로 매끄럽습니다. 1에 가까운(그러나 그보다 낮은) 값도 장기적으로는 드리프트가 아니라 평균 복귀하는 경향이 있습니다. 따라서 단위근 프로세스는 근값이 1에 매우 가까운 프로세스와 근본적으로 다르다는 점에서 특별합니다.
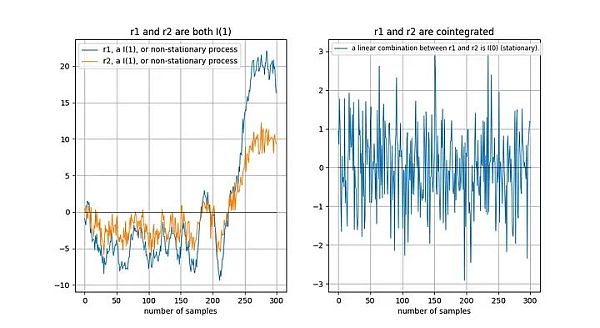
두 임의 변수(이 경우 시계열) 간의 공분산(공분산 관계)의 존재 유무 . 두 변수가 공적분을 이루려면 두 변수의 적분 순서가 같아야 하고 둘 다 비고정적이어야 합니다. 또한 (그리고 이것이 핵심 부분입니다) 두 시계열의 선형 조합이 매끄러워야 합니다.
두 시계열이 비고정적인 경우 선형 조합(이 경우 단순히 두 시계열 간의 차이를 선택)도 일반적으로 비고정적입니다.

두 비고정 시계열이 장기적으로 "같은 방식으로" 드리프트하면 선형 조합(이 경우 r2- 0.5*r1을 선택)도 비고정일 수 있습니다:
이것이 공분산 신호의 좋은 예입니다. 0.5*r1)은 평활할 수 있습니다:
Tu 등[1]은 공적분 관계를 직관적으로 설명합니다:
"시계열 간의 공적분 관계의 존재는 장기적으로 공통의 확률적 드리프트를 공유한다는 것을 의미합니다. 장기적으로 공통의 확률적 드리프트를 가지고 있습니다."
평활하지 않은 두 시계열의 선형 조합이 왜 평활할까요? x와 y라는 두 시계열이 있고 x를 기준으로 y를 모델링하려고 한다고 가정해 보겠습니다. 모델 오차는 x와 y의 선형 조합에 의해 주어집니다: 모델 오차 = y - a - b*x. 우리는 모델 오차가 매끄러워야 합니다. 즉, 시간이 지남에 따라 변동하지 않기를 원합니다. 시간이 지남에 따라 모델 오차가 달라진다는 것은 모델이 잘못되어 정확한 예측을 할 수 없다는 뜻입니다.
잉글과 그랜저[2]의 "공적분과 오류 수정: 표현, 추정, 테스트"(그랜저는 공적분 개념을 창안한 인물로 2003년 노벨 경제학상을 수상했다)에서는 다음과 같이 정의하고 있습니다. 공적분학의 주요 개념과 테스트. 이 논문의 핵심은 시계열이 확률적이며 결정적 요소가 없다는 가정입니다(이에 대해서는 나중에 다시 설명하겠습니다).
결정론적 추세가 있는 경우 분석 전에 이를 제거해야 합니다:

시간 기반 파워 법칙에는 두 가지 변수가 있습니다.
1. log_time: 블록 생성 이후 일수의 로그
2. log_price: 가격의 로그
3. >
Engle과 Granger의 정의에 따르면, 두 변수는 결정적 요소가 없는 랜덤 변수여야 하며 평활하지 않아야 합니다. 또한 이 두 변수의 정적 선형 조합을 찾을 수 있어야 합니다. 그렇지 않으면 두 변수 간의 공적분은 발생하지 않습니다.
자세히 알아보기 전에 평활화나 공적분 개념이 포함되지 않은 모델 데이터 자체의 그래프를 몇 개 보여드리겠습니다. 시간 기반 파워 법칙을 사용하면 직관적으로 꽤 잘 맞는다는 것을 알 수 있습니다. 잔차 벡터(잔차 벡터)는 드리프트를 즉시 표시하지 않습니다.
이미지 src="https://img.jinse.cn/7198484_image3.png">
또한 이 모델은 뛰어난 표본 외 성능을 보여줍니다(아래 참조). 표본 외 성능이 우수하다고 해서 모델이 가짜라는 의미는 아닙니다. 가짜 상관관계에 기반한 모델은 단지 가짜, 즉 정확한 예측이 불가능할 뿐입니다. 표본 외 성능을 테스트하는 방법은 제한된 양의 데이터(특정 날짜까지)에 모델을 맞추고 모델이 맞지 않는 기간에 대해 예측(교차 검증과 유사)을 하는 것입니다. 표본 외 기간 동안 관측 가격은 모델 가격을 자주 교차하며, 관측 가격의 최대 편차가 모델 가격에서 체계적으로 더 멀어지지 않습니다.
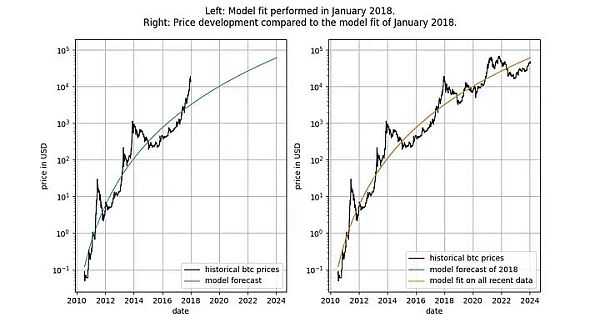
모델 출시(2019년 9월) 이후에는 부정행위가 있을 수 없기 때문에 더 엄격하게 성과를 살펴볼 수 있습니다. - 사후에 모델을 변경할 수 없습니다.
이미지 src="https://img.jinse.cn/7198486_image3.png">
누군가가 이 모델이 가짜 상관관계에 불과하다고 비난한다면, 이미 모델의 예측력을 의심해봐야 합니다.
로그_시간과 로그_가격 간에 공적분이 가능하려면 두 변수가 같은 차수, 적어도 차수 1의 확률 변수여야 합니다.
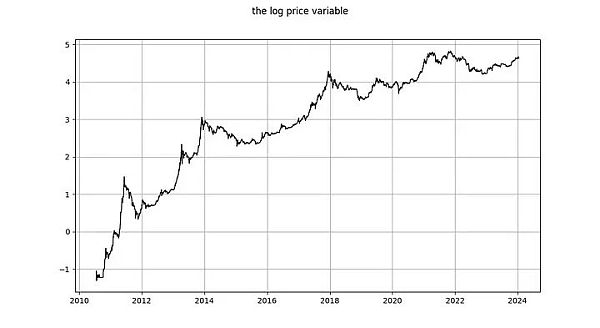
로그_가격이 평활화된 시계열입니까? Nick은 지정되지 않은 유형인 ADF 테스트(비정형성 테스트)와 KPSS 테스트(정규성 테스트)를 통해 로그(가격)가 의심할 여지 없이 비정형이며 따라서 I(1) 이상이라는 결론을 내립니다. 마르셀 버거는 육안 검사로 I(1)이라는 결론을 내립니다. 팀 스톨테는 더 흥미로운 관찰을 합니다: 그는 다른 기간에 대해 ADF 테스트를 실행하고( 유형이 지정되지 않음)를 실행하고 "따라서 우리는 비정규성을 단호하게 거부하고 로그 가격에 비정규성의 징후가 있다고 결론을 내릴 수 없다"며 상황이 명확하지 않다고 지적했습니다.
자체 분석을 실행해 봅시다. 팀 스톨테와 마찬가지로, 항상 사용 가능한 첫 번째 날짜부터 시작하여 매일 하루를 추가하는 방식으로 다양한 시간대에 ADF 테스트를 실행합니다(일일 데이터를 사용). 이렇게 하면 시간이 지남에 따라 ADF 테스트 결과가 어떻게 변하는지 확인할 수 있습니다. 하지만 팀과 닉과는 달리 우리는 어떤 버전의 ADF 테스트를 실행할지 지정해야 합니다. 위키백과에 따르면 DF 및 ADF 테스트에는 세 가지 주요 유형이 있습니다.
p>이 세 가지 버전의 차이점은 서로 다른 추세를 수용(제거)할 수 있다는 것입니다. 이는 결정론적 추세를 제거해야 한다는 Engle과 Granger의 요구 사항과 관련이 있는데, 세 가지 버전은 세 가지 간단한 유형의 결정론적 추세를 제거할 수 있습니다. 첫 번째 버전은 과거 로그 가격 데이터만을 사용하여 일일 로그 가격 변화를 설명하려고 시도합니다. 두 번째 버전은 상수 항을 사용할 수 있으며, 그 결과 log_price가 선형 추세(상승 또는 하락)를 가질 수 있습니다. 세 번째 버전은 이차(포물선) 구성 요소를 허용합니다.
팀과 닉이 어떤 버전을 실행하고 있는지 알 수 없지만 세 가지 버전을 모두 실행해 보겠습니다.
ADF 테스트에서 사용하는 최대 지연은 1이지만 더 긴 지연을 사용한다고 해서 결과와 결론이 의미 있게 달라지지는 않습니다. "최대 지연"을 1로 설정하고 "회귀" 매개변수에 "n", "c" 및 "ct"를 사용하는 Python의 statsmodels.tsa.stattools.adfuller 함수를 사용합니다(위의 Wikipedia에서 설명한 세 가지 유형과 동일). 아래 그림에는 테스트에서 반환된 p값(통계적 유의성의 척도)이 표시되어 있으며, p값이 작을수록 평활화 가능성이 높음을 나타냅니다(일반적으로 사용되는 임계값은 0.05입니다).
이미지 src="https://img.jinse.cn/7198489_image3.png">
첫 번째 방법(녹색 선)은 로그 가격 시계열이 평활화되지 않았다는 결론을 내립니다. 세 번째 테스트(주황색 선)는 동일한 결론에 도달하지만 덜 결정적입니다. 흥미롭게도 상수 항을 허용하는 테스트(파란색 선)는 시계열이 평활한지 여부를 판단하지 못합니다(Tim도 상수 항이 있는 ADF 테스트를 사용하는 것 같습니다). 세 버전이 이렇게 다른 이유는 무엇이며, 특히 상수 항이 있는 버전에서 로그 가격이 평활하다는 것을 배제할 수 없는 이유는 무엇일까요?
단 한 가지 설명이 있습니다. log_price 차이에 상수 항만을 사용하면(로그_가격에 선형 항이 생기므로) 시계열에 '매우 잘' 맞아서 거의 매끄럽게 보이는 잔여 신호가 생성됩니다(시작점과 끝점의 편차가 상당히 크지만). log_price에 결정론적 추세를 전혀 사용하지 않거나 이차 용어 결정론적 효과를 사용하는 것은 훨씬 덜 효과적입니다.
이미지 src="https://img.jinse.cn/7198490_image3.png">
이것은 이미 시간과 log_price 사이에 관계가 있다는 강력한 힌트를 제공합니다. 실제로 상수 항을 사용한 ADF 테스트에서 신호가 평활하다는 결론이 나온다면, 이는 선형 시간 항이 로그_가격에 충분히 근접하여 평활 잔차를 얻을 수 있다는 것을 의미합니다. 매끄러운 잔차를 얻는 것은 스퓨리어스가 없는 관계(즉, 올바른 설명 변수를 찾았다는 의미)의 신호이기 때문에 바람직합니다. 선형 시간 추세는 우리가 원하는 것과 정확히 일치하지는 않지만, 우리는 그것에 접근하고 있는 것 같습니다.
우리의 결론은 (다른 게시물에서) 다음과 같이 말한 마르셀 버거의 결론과는 확연히 다릅니다."이전 분석에서 저는 비트코인 가격이 1차 통합임을 보여줬고, 이는 여전히 유효합니다. 비트코인은 시간이 지남에 따라 가격이 변하는 데 결정적인 요인을 보이지 않습니다."
선형 시간은 시간에 따른 비트코인 가격의 움직임을 적절히 설명하지 못하지만, log_price에 결정적 시간 요인이 있다는 것은 분명하다는 결론을 내렸습니다. 또한 적절한 결정론적 요소를 제거한 후에도 (Engle과 Granger가 요구한 대로) log_price가 I(1)이라는 것도 명확하지 않습니다. 대신 추세 평활화된 것처럼 보이지만 여전히 적절한 결정적 요소를 찾아야 합니다.
공적분을 찾고 있는 경우, 두 변수가 공적분이 되려면 둘 다 I(1) 이상이어야 하므로 log_price가 I(1)이 아닌 것은 이미 문제가 됩니다.
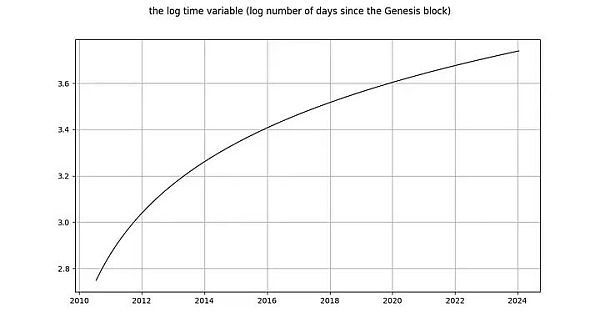
이제 log_time 변수를 살펴보겠습니다. Marcel Burger는 log_time이 6차 적분을 수행하는 것 같다는 결론을 내렸습니다(그는 수치 문제에 부딪히기 전까지 미분을 수행하고 있었습니다). 그는 log_time과 같은 수학 함수가 완전히 결정론적인 변수에서 무작위 변수로 변환될 수 있다고 예상했는데, 이는 말이 되지 않는다고 생각했습니다.
log_time에 대한 Nick의 결론은 log_price 변수에 대한 결론과 동일합니다. log_time이 비평활성이므로 I(1) 이상이라는 것은 의심의 여지가 없습니다. 팀 스톨트는 log_time이 구조상 비평활성이라고 주장합니다. 이러한 주장은 놀랍습니다! 적분 순서와 공분산은 결정론적 경향이 제거된 확률 변수의 개념을 말합니다(위의 Engle과 Granger [2] 참조). 한 가지 주의할 점은 결정론적 변수의 값은 미리 알 수 있지만, 무작위 변수의 값은 그렇지 않다는 것입니다. 시간은 로그 함수와 마찬가지로 (당연히) 완전히 결정론적이며, 따라서 log_time도 마찬가지입니다.
이미지 src="https://img.jinse.cn/7198492_image3.png">
그림 캡션: 왼쪽: 제네시스 블록 이후 이후 일수의 로그는 완전히 결정론적입니다. 오른쪽: 랜덤 변수(왼쪽의 결정론적 변수와 약간 비슷해 보임).
엥글과 그레인저의 접근 방식을 따라 log_time에서 결정적 추세를 제거하면 log(x) - log(x) = 0, 즉 완전히 결정적인 신호가 남게 되므로 0의 벡터만 남게 됩니다. 즉, 완전히 결정론적인 변수인 log_time을 무작위 변수로 변환할 수 없으므로 Engle과 Granger의 프레임워크를 사용할 수 없는 곤경에 처하게 됩니다.
공적분 분석에서 완전 결정론적 변수가 얼마나 문제가 되는지 알아보는 또 다른 방법은 디키-풀러 검정과 같은 평활성 검정이 어떻게 처리하는지 생각해 보는 것입니다. 가장 간단한 경우(여기서 y는 관심 변수, rho는 추정할 계수, u는 백색 잡음으로 가정한 오차 항)를 고려해 보겠습니다.
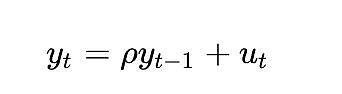
어떻게 될까요? 임의의 성분이 없으므로 오차 항 u_{t}는 모든 t 값에 대해 0이 됩니다. 하지만 로그_시간은 시간의 비선형 함수이므로 rho의 값도 시간에 따라 달라져야 합니다.
랜덤 변수의 경우 이 모델이 더 유용한 이유는 변수 rho가 이전의 임의 값이 기억된 정도를 포착하기 때문입니다. 그러나 임의의 값이 없는 경우 이 모델은 의미가 없습니다.
결정론적 변수에 대한 다른 유형의 테스트에서도 동일한 문제가 존재합니다.
따라서 완전히 결정론적인 변수는 공적분 분석에 포함되지 않습니다. 다시 말해, 공적분 분석은 결정론적 신호에는 적용되지 않으며, 신호 중 하나가 결정론적이라면 공적분 분석은 가짜 관계가 있다고 주장하는 시대착오적인 도구입니다.
공적분 관계는 두 변수가 모두 I(d)이고 d가 적어도 1인 경우에만 존재합니다. log_time은 완전히 결정론적인 변수이며 정적 테스트에서는 사용할 수 없다는 것을 보여주었습니다. log_time이 I(0), I(1) 또는 I(6)인지는 알 수 없습니다. 또한 log_price는 I(1)이 아니라 추세 평활화되어 있습니다.
log_time과 log_price 사이에 공적분이 없는데, 이는 시간 기반 파워 법칙이 통계적으로 유효하지 않거나 가짜라는 것을 의미합니까?
정확히 아닙니다
올바른 통계 분석에서는 결정론적 변수와 추세 평활화 변수를 혼합하여 사용하는 것이 옳습니다. 공적분은 비평가들이 믿게 하려고 하는 것처럼 통계적 관계 분석의 핵심이 아닙니다.
따라서 공적분 분석은 실현 가능하지 않습니다. 그러나 전력법 모델에 평활화 분석을 적용할 수 있는 여지가 있을 수 있습니다. 이 문제에 대해 자세히 살펴보겠습니다.
우리가 입력 변수의 공적분 분석을 시작하는 이유는 두 변수의 부드러운 선형 조합을 찾고 싶기 때문입니다. 결정론적 변수(log_time)와 추세 평활 변수(log_price)를 결합하여 평활 변수를 얻는 것은 근본적으로 불가능합니다. 따라서 엄격한 의미에서 공적분을 찾는 대신 잔차에 대해 평활성 테스트를 수행할 수 있습니다(잔차는 단순히 두 입력 신호의 선형 조합이므로). 잔차가 평활하다면 엥글-그랜저 공적분 테스트를 엄격하게 따르지 않더라도 평활한 선형 조합을 찾은 것입니다(이것이 바로 공적분의 핵심입니다).
James G. MacKinnon[3]은 그의 논문 "공적분 테스트의 임계값"에서 이를 정확히 이렇게 설명합니다: "공적분 회귀"(log_time과 log_price를 연관시키는 회귀)를 수행하면 Engle-Granger 공적분 테스트를 엄격히 따르지 않아도 부드러운 선형 조합(공적분의 목적이 되는)을 찾을 수 있다는 것이죠. "공적분 회귀"(로그_시간과 로그_가격을 연결하는 회귀)를 수행한 경우, 공적분 검정(Engle-Granger 검정)은 잔차의 평활성 검정(DF 또는 ADF 검정)과 동일합니다.


따라서 결과 테스트 통계를 제외하고는 동일한 두 가지 방법 중 하나를 사용할 수 있습니다.
1. log_time을 log_price에 맞추고 잔차(오류)를 계산합니다. 잔차에서 DF를 계산하거나 더 나은 방법으로는 ADF 테스트를 계산합니다. 결과 통계는 잔차가 평활한지 여부를 나타냅니다.
2. log_time과 log_price가 I(1)이라고 가정하고 엥겔-그랜저 공적분 테스트를 실행합니다. 결과 통계는 잔차가 평활한지 여부를 나타냅니다.
ADF 테스트의 경우 파이썬의 statsmodels.tsa.stattools.adfuller 함수를 사용하고, 잉글-그랜저 테스트의 경우 statsmodels.tsa.stattools.coint를 사용합니다. 두 함수 모두에 대해, 우리는 상수를 사용하지 않는 이유는 잔차에 시간이 지남에 따라 일정한 드리프트가 있어서는 안 되기 때문입니다(시간이 지남에 따라 모델이 가격을 과대 또는 과소 평가하기 시작한다는 의미이므로).
ADF 검정과 잉글-그랜저 검정이 동일하다고 썼지만 그렇지 않습니다. 잉글-그랜저 공적분 검정은 N=2개의 확률 변수가 있다고 가정하는 반면, ADF 검정에서는 N=1개의 확률 변수가 있다고 가정합니다(N은 자유도를 나타내는 척도입니다). 무작위 변수는 다른 무작위 변수나 결정적 변수의 영향을 받을 수 있지만, 결정적 변수는 무작위 변수의 영향을 받을 수 없습니다. 따라서 이 사례(결정론적 변수 로그_시간이 하나만 있는 경우)에서는 ADF 테스트에서 반환되는 통계(N=1 무작위 변수를 가정)가 더 바람직합니다. 원칙적으로 잉글-그랜저 검정과 ADF 검정은 서로 다를 수 있지만, 시간 기반 모델에서는 실제로 그렇지 않습니다. 아래에서 볼 수 있듯이 결론은 동일합니다. 잔차의 부드러운 벡터를 얻을 수 있습니다. 두 테스트의 점수는 모두 임계값인 0.05보다 훨씬 낮으며(잔차가 매끄럽다는 것을 나타냄), 오랫동안 그렇게 유지되어 왔습니다.
이미지 src="https://img.jinse.cn/7198495_image3.png">
그림 캡션: ADF에 기반한 잔류성 잔류성 잔류성 잔류성 잔류성 잔류성 잔류성 잔류성 및 엥글-그랜저 테스트 결과, 시간 기반 전력법칙은 2016년경부터 잔차가 완만해집니다.
두 테스트 모두 처음에는 평활 잔차가 정상임을 보여줍니다. 이는 잔류 신호의 저주파 성분이 매끄럽지 않은 신호로 오인될 수 있기 때문입니다. 시간이 지나야만 잔류 신호의 평균 복귀가 명확해지고 실제로 부드러워집니다.
S2F 모형은 입력 변수가 (부분적으로) 결정된다는 시간 기반 파워 법칙과 유사한 이유로 엄격한 의미의 공적분은 불가능하기 때문에 일반적으로 거부되어 왔습니다. 그러나 이 모델은 매우 매끄럽게 보이는 잔차를 생성합니다.
이미지 src="https://img.jinse.cn/7198496_image3.png">
실제로 잉글-그랜저 공적분 검정과 ADF 안정성 검정(결정변수와 확률변수가 존재하기 때문에 선호되는 검정)은 모두 0에 매우 가까운 p값을 산출합니다. 따라서 "공적분 부족"(실제로는 "평활성 부족")을 이유로 S2F 모델을 배제해서는 안 됩니다.
그러나 2020년 초에 언급했듯이, S2F 모델이 유효하지 않다는 다른 징후도 있습니다. BTCUSD의 가격이 S2F 모델이 예측한 것보다 낮을 것이라는 저희의 예측은 선견지명이 있는 것으로 판명되었습니다.
시간 대비 장기 주가 지수(이 경우 배당금 재투자를 제외한 S&P 500)를 살펴보는 것도 흥미롭습니다. 주요 주식 시장 지수는 평균 약 7%의 기하급수적인 속도로 성장한다는 것은 잘 알려져 있습니다. 실제로 지수 회귀를 통해 이를 확인할 수 있습니다.
이미지 src="https://img.jinse.cn/7198497_image3.png">
여기서 우리는 또 다른 결정적 변수(시간)를 만나게 됩니다. 잉글-그랜저 공적분 검정은 약 0.025의 p-값을 산출하고, ADF 검정(선호)은 약 0.0075의 p 값이 약 0.0075로 나옵니다(하지만 이 값은 선택한 정확한 기간에 따라 크게 달라집니다). 다시 한 번, 잔차를 평활화합니다. 주가의 지수 시간 추세가 유효합니다.
S2F 모델은 처음에는 계량경제학적 기초, 특히 공적분의 존재로 인해 (특히 마르셀 버거와 닉 엠블로우에 의해) 높은 평가를 받았습니다. 시류가 바뀌면서 S2F 모형이 엄격한 의미에서 공적분 관계가 없다는 것이 분명해졌고, 마르셀과 닉은 S2F 모형이 유효하지 않다고 선언하며 배에서 뛰어내렸습니다. 이 사건 이후 S2F 모델에 대한 대중의 시각이 바뀐 것으로 보이는데, 에릭 월이 사건의 전환에 대해 짧게 요약한 글을 올렸습니다.
우리는 공적분과 평활성이 거의 같은 의미로 사용될 수 있다고 설명했고, 계량경제학 문헌(MacKinnon [3])도 이에 동의합니다(통계의 값을 제외하면). 이러한 견해에 따라 공적분/평활성 측면에서 S2F 모델에 어떠한 문제도 없다고 생각하며, 따라서 공적분성이 부족하다는 주장 때문에 S2F 모델에 대한 우리의 견해를 바꾸는 것은 잘못된 것입니다. 저희는 S2F 모델이 잘못되었다는 데 동의하지만, 이는 코인 통합 부족이 아닌 다른 이유에서 잘못된 것입니다.
비트코인의 시간 전력법 모델은 공적분 부족으로 인해 로그_시간과 로그_가격 사이의 관계를 가짜로 표시한다는 비판을 받아왔습니다. 비트코인의 시간 기반 전력법 모델의 잔차는 분명히 매끄럽다는 것을 보여 주었기 때문에 비판자들의 논리는 의문입니다.
비트코인의 시간 기반 전력법 모델은 유효하고 안정적이며 강력합니다. 언제나 그렇듯이.
참고자료
1. "범용 코인 통합과 그 응용" Tu et al. 보충 정보
2."공동 통합 및 오류 수정: 표현, 추정 및 테스트" Tu et al. 추정, 그리고 테스트"
3. " 코인통합 테스트의 임계값" by James G. MacKinnon
비트코인은 일반적인 자산이라기보다는 자연 현상에 가깝습니다. 비트코인은 금융 자산이라기보다는 하나의 도시이자 유기체와 비슷합니다.
 JinseFinance
JinseFinance시가총액 기준 상위 20개 암호화폐는 F부터 S까지 등급을 매겨 순위를 매깁니다. 시가총액 기준 상위 20개 암호화폐는 F부터 S까지 등급을 매깁니다.
 JinseFinance
JinseFinance비트코인의 시간 기반 힘의 법칙 모델은 그 어느 때보다 유효하고 안정적이며 강력합니다.
 JinseFinance
JinseFinance JinseFinance
JinseFinance40개 이상의 네트워크를 지원하는 저명한 암호화폐 채굴 풀인 F2pool의 세계에 대해 알아보세요. F2pool의 설립 배경, 글로벌 입지, 지급 방식, 안전하고 수익성 있는 채굴을 위한 최고의 선택인 이유를 알아보세요.
 Huang Bo
Huang BoXterio는 현금을 사용하여 AI용 애플리케이션을 탐색하고 새로운 토큰을 출시할 계획입니다.
 TheBlock
TheBlock채굴자는 거래 비용을 지불하기 위해 거의 3천만 gwei를 사용했습니다.
 Coindesk
CoindeskDigiDaigaku는 실제 게임 기능(출시되지 않음)을 가질 뿐만 아니라 Paradigm, FTX, Coinbase 등과 같은 유명 개인 및 벤처 캐피탈 회사로부터 자금을 지원받습니다. 프로젝트 파티는 수년간 모바일 게임 분야에 종사해 온 Web2 시니어 팀 그룹이 설립한 Limit Break라는 Web3 게임 개발 회사입니다.
 Nell
Nell이스라엘 연구원들이 채굴 풀이 더 높은 채굴 보상을 얻기 위해 이더리움 블록 타임스탬프를 조작하고 있다고 주장한 후에 응답이 나왔습니다.
 Cointelegraph
Cointelegraph비트코인 S2F 모델은 강세장 절정기에 많은 인기를 얻었고 비판도 있었지만 가격이 차트를 따라가는 것 같아서 대부분 무시됐다.
 Cointelegraph
Cointelegraph