Author: Jeff Emmett, Medium; Translator: Blockchain Robin, Chain Academy
Originally published on the BCRG mirror, this article compares two different bond curve applications that play an important role in the token ecosystem. The article will introduce the bond curve as the core mechanism of the automated market maker (AMMs) and explore the basics of primary automated market makers (PAMMs*) and secondary automated market makers (SAMMs*) and the differences between the two. This article is part of a larger effort to clarify and define the design space of the bond curve so that these tools can be applied responsibly.
The Bonding Curve Research Group (BCRG) initially collaborated with the Token Engineering Public Domain to advance research, development and education around the topic of the bond curve, especially in its use as a dynamic issuance mechanism for crypto tokens and as a tool for creating more valuable stable and sustainable token economies.
*Note: The terms SAMM and PAMM were originally proposed by researchers at Gyroscope, an algorithmic stablecoin built using these mechanisms.
Bonding Curve OverviewBonding curves have been a fascinating topic of discussion in the Web3 space over the past few years. Their use in DeFi products, such as decentralized exchanges, has revolutionized token liquidity and facilitated large-scale trading of small-cap tokens in a way that was not previously possible. In short, the crypto ecosystem would not be where it is today without the help of bonding curves. While many token ecosystems have leveraged the benefits of these tools, how they work, or why they are so important, remains a mystery to most users.
So what is a bonding curve? A bonding curve is a mathematical encoding of the relationship between two or more tokenized assets. Enabled by smart contracts running on a blockchain, the most basic bonding curve allows these assets to be traded against each other, with the bonding curve defining their exchange rate. A popular example of a bonding curve equation is “X * Y = K”, where there is an “invariant K” that defines the exchange price between token X and token Y. As the supply of either token increases or decreases, the “curve” defines how the price changes. As we will see, bonding curves can be applied in different contexts and configurations, providing critical infrastructure for projects deploying token economies.
Bonding Curve Applications in Market DesignMost of the bonding curves in use today are embedded into automated market makers like Uniswap, Balancer, or Curve, where their primary function is to facilitate the exchange of existing tokens through “liquidity pools”. These mechanisms can be considered secondary AMMs (or SAMMs) because their purpose is to facilitate secondary market exchange between already existing tokens. A large amount of literature has been written about this application of bonding curves, and many different invariant functions have been tried for various purposes.
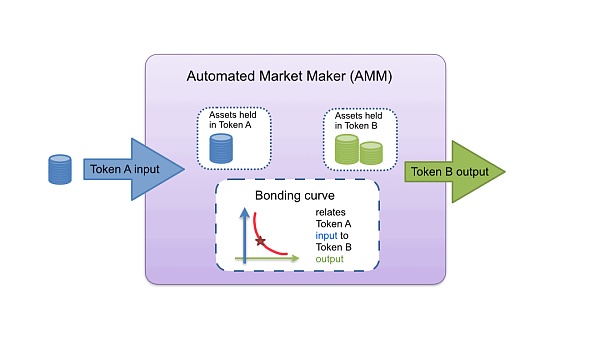
Another use of bonding curves is to directly issue (mint) and redeem (burn) tokens. These mechanisms can be considered primary AMMs (or PAMMs) because they are the “source” for token issuance, when reserve assets are deposited, and the “sink” for token redemption, when reserve assets are withdrawn from the bonding curve. PAMMs enable a dynamic supply token ecosystem and can be considered a “supply discovery” mechanism for tokens deployed using these tools.
PAMMs address some of the key challenges of token design today, such as projects having to guess how many tokens their system will need over the life of the system. By allowing for a dynamic token supply based on market demand, PAMMs not only streamline the early decision-making process, but can also serve as an ongoing fundraising tool for productive projects, owning all of the protocol’s liquidity by default.
We’ll briefly dive into both of these use cases for bonding curves to understand the benefits they provide to token ecosystems, and briefly explore how they combine to provide a range of critical infrastructure for token ecosystems of all sizes.
SAMMs as Price Discovery Mechanisms: Initial Product-Market FitThe rise of decentralized finance (DeFi) has led to the development of AMM platforms like Uniswap, Balancer, and Curve, which replace traditional order book trading with asynchronous swaps through “liquidity pools.” These liquidity pools allow token holders to deposit selected tokens into a smart contract for traders to easily swap between assets in the pool based on the pricing algorithm set by the bonding curve.
These new market structures improve on several aspects of order book trading: they are non-custodial (since no exchange is required to hold funds on behalf of the user), they are asynchronous (since orders from buyers and sellers do not need to be matched directly but can be routed to a pool), and most importantly, the fees paid by traders do not go to some intermediary exchange but rather flow back to the liquidity providers themselves.
Before the advent of secondary AMMs, the only tokens with consistent trading volume (and thus trading liquidity) were Bitcoin, Ethereum, and possibly a handful of others. Most of the tokens that existed were barely tradable, and they had many issues with price discovery due to low volumes and thin order books. DApps like Uniswap provide a platform that makes SAMMs easy to deploy, allowing a large number of small-cap tokens to find some level of trading liquidity. SAMMs were the first product-market fit moment for the bonding curve, providing price discovery and trading liquidity for most tokens, and we believe there are more to come.
PAMMs as Supply Discovery Mechanisms: The Power of Dynamic Token IssuanceImagine you want to run a theme park, but before you can start operations, you need to determine the number of ride tickets that will satisfy customer demand 15 years from now. Sound impossible? This is more or less how most token issuances work today, with development teams setting predefined token issuance schedules that sometimes stretch over hundreds of years.
With rudimentary AMMs, token ecosystem designers no longer have to guess how many tokens their ecosystem will need, and at what growth rate.
Unlike SAMMs, PAMMs facilitate the minting and destruction of tokens using a bonding curve, thus providing an automated issuance and redemption mechanism for dynamic token supply. PAMMs are a “supply discovery” tool (vs. the “price discovery” function of SAMMs) that solve several potential incentive misalignment issues in token ecosystem design and launch. By adjusting token supply based on demand, and holding deposited assets through an automated smart contract reserve, PAMMs ensure that each token has its redemption value backed by a certain percentage of reserve assets.
Why Dynamic Token Issuance? Most tokens deployed today fall on two extremes of the issuance spectrum: fixed supply at one end, and unlimited supply at the other. Each of these issuance paradigms has advantages and disadvantages, and is used for different reasons. Fixed supply tokens provide some assurance to holders that the token will not be diluted through additional issuance — however, the rigidity of a fixed supply can limit the ability of the ecosystem to allocate tokens in response to emerging demand for the network. On the other hand, unlimited supply tokens can incentivize behaviors such as staking by offering token rewards, but if network productivity (and token price) do not grow with supply increases, unconstrained supply increases may dilute existing token holders and reduce trust in the token.
The PAMM Bonding Curve sits in the middle ground between these two extremes, leveraging the best of both worlds by providing the flexibility of dynamically issued supply expansion while constraining that supply expansion to be tied to deposits of reserve assets. This enables PAMMs to provide projects with a flexible token supply that can meet growing (or shrinking) demand while maintaining token value.
Dynamic issuance enables the token supply to expand as demand for a particular service grows, while still ensuring that each token in the supply is backed by an asset at a certain ratio - a guarantee built into the PAMM issuance mechanism through the bonding curve invariant itself.

Sponsored Business Content
PAMMs include two basic mechanisms:
Funding for Minting: Participants deposit reserve assets (such as USDC or ETH) into the PAMM smart contract reserve pool, which then mints a corresponding number of tokens based on the price currently reported by the bonding curve invariant and sends them to the participant.
Destruction for Withdrawal: Participants can destroy some of their tokens by selling tokens to the PAMM and redeeming them for reserve assets (such as USDC or ETH). This redemption price is defined by the bonding curve invariant.
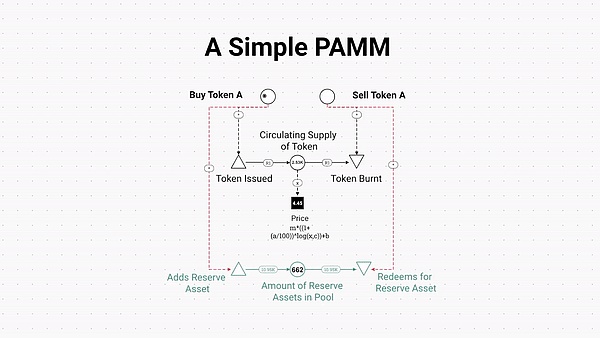
PAMM Machinations model, where tokens are issued and burned based on deposits and withdrawals of reserve assets in the PAMM reserve.
There are already many PAMMs deployed and existing in the wild today, although terminology and customization can vary greatly between different teams using these tools. The Bonding Curve Research Group has begun a series of case studies of various implementations of PAMM-like tools to understand the strengths and weaknesses of these mechanisms in live deployments. We intend to add to the discourse around best practices for the design and configuration of these curves, providing a useful blueprint for others. We aim to establish data structures for analytical modeling and simulation of these new tools, and share lessons learned across implementations.
Promising Benefits of Combining PAMMs and SAMMsLeaving aside the specific mechanics of PAMMs and SAMMs, these tools can provide further benefits to the token economy when used in conjunction within an ecosystem. The simultaneous existence of primary issuance and secondary exchange markets provides opportunities for arbitrage when these markets diverge in value, which can ultimately be beneficial to the system as a whole if designed properly.
If the price of a token on a SAMM is higher than the minting price on a PAMM, any participant can mint new tokens on a PAMM by depositing reserve assets, thereby increasing the token supply (and price) on the primary market. They can then sell these tokens on a SAMM for a higher price than they just bought them for, thereby lowering the token price on the secondary market. This action helps align the two market prices by increasing the token supply in response to demand, while arbitrageurs pocket the difference for their corrective action of increasing token supply.
This also works in the other direction - if a token is trading on a SAMM for less than the burn price on a PAMM, anyone can buy these tokens on the secondary market at the lower price and burn them back to the primary market in exchange for the underlying reserve assets, again pocketing the price difference. This will also bring the prices of the two markets closer together and reduce the supply of tokens in response to the lack of demand for that token.
While these actions may not seem particularly exciting in themselves, the resulting systemic effects should be of interest to token designers. This effect is demonstrated in the token price chart below.
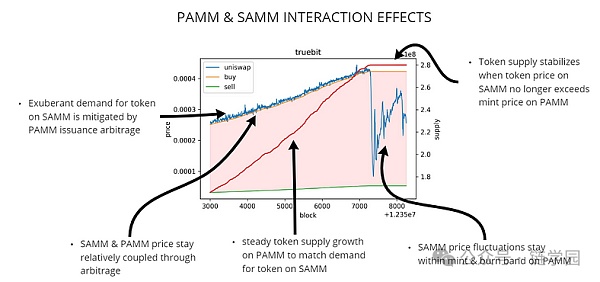
A real-time example of PAMM and SAMM interactions dampening token price volatility in the Truebit token ecosystem. In the figure, the blue line represents the SAMM price of the TRU token, the orange line represents the PAMM price of the same token, and the red line represents the supply of the token. Data and charts by @banteg, with comments and illustrations by Jeff Emmett.
The above chart shows the price volatility dampening effect of PAMMs and SAMMs in the existing token ecosystem. As described above, when the token price on the SAMM exceeds the minting price on the PAMM, market participants respond to demand on the SAMM by increasing the token supply by depositing reserves (ETH in this case) on the PAMM, and selling this increased supply to demand on the SAMM at a profitable price. These actions not only keep prices consistent between the primary and secondary markets, but also smooth out what could have been a speculative pump and dump into a smoother, more stable price increase. (The subsequent price drop is another entirely different design consideration.)
Essentially, the combination of PAMMs and SAMMs in a token ecosystem can have a “volatility mitigation” effect on token prices. This effect has been observed in models as well as in actual deployments, although further research is needed into the limitations and potential drawbacks of these effects.
While further exploration of these benefits will have to await a follow-up article, the potential for these tools to address some of the key challenges of the crypto token economy—such as reducing excessive price volatility—is very promising and worthy of further investigation.
Conclusion and Future ResearchBonding curves are already an important part of the Web3 space, and their importance will only continue to grow. PAMMs and SAMMs have proven themselves useful for token economies large and small. Whether bootstrapping early-stage token ecosystems or facilitating exchange in mature ecosystems, bonding curves, in their various forms and functions, will continue to play a critical role in the digital economy.
The exploration and research of bonding curves is in its infancy. While there has been much written and deployed in the space of SAMMs (although not often under that name), PAMMs are still fairly new and under-researched. In order to build a socially responsible and robust digital public infrastructure, which is a necessary engineering discipline, developers building these new technologies must continue to support token engineering research, development, and education—particularly the continued research of bonding curves.
The Bonding Curve Research Group looks forward to continuing its research with further funding from a range of research partners. Our research roadmap includes further case studies and empirical analysis of existing PAMMs, exploring the relationship between PAMMs and SAMMs, simulating their interactions, and more to uncover the benefits of these fascinating curves. Our future publications will touch on the tangible benefits these new tools bring to projects and users, dive into some of their existing deployments, and even explore how they replicate processes found in nature.
This ongoing research will greatly advance our understanding of these new tools and their huge potential to solve the challenges facing DeFi (and ReFi) to have a lasting, positive impact on the world.
This article was written by Jeff Emmett, Jessica Zartler, and Curiousrabbit, with contributions from Jakob Hackel, and special thanks to Token Engineering Commons for funding this first round of research.
 JinseFinance
JinseFinance












