Author: Arweave Oasis, Source: PermaDAO
This article is a bit hardcore, because there will be a lot of mathematical derivation and argumentation, friends should be prepared. But the author believes that mathematics, as a basic subject, has a strong accuracy in logically explaining a thing, so let me try to use simple language to show the beauty of mathematics in the @ArweaveEco mechanism.
In White Paper Interpretation (II) Article, we described the Succinct Access Proof (#SPoA) game that can be used by any participant to prove that they do store some data in a specific location in a data set. This pattern can also be used to create a second game, which we call Succinct Proofs of Replications (SPoRes), which will allow the prover to prove to the verifier that they have stored a certain number of copies of the data, regardless of the size of the dataset, with minimal data transfer and verification costs.
SPoRes Game
The Succinct Proofs of Replication (SPoRes) game is played like this. Alice claims that she stores n unique copies of the Merkle-ized dataset. Bob wants to verify that Alice is not lying. To do this, he gives Alice a difficulty parameter d and a randomly generated seed Seed. Alice uses this seed to generate a VDF hash chain that issues a checkpoint every second, which can be used to unlock up to k SPoA challenges in the dataset. Whenever she has a packaged data block corresponding to these challenges, Alice can construct the corresponding SPoA proof. These proofs are then hashed and compared with Bob's difficulty parameter d. If the proof hash value is greater than d, Alice has found a valid solution and sends the corresponding proof to Bob. Bob records the time between sending the random seed and receiving Alice's valid proof.
Based on the difficulty d, the probability p of finding a valid solution in a single attempt is expressed as:
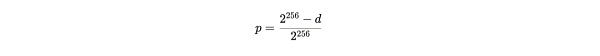
Formula Notes:Since the SHA 256-based algorithm is a 256-bit string, there are 2^256 (where "^" means the power) maximum hash numbers. If you want to find a valid solution greater than d, there are only 2^256-d hash numbers, which can be used to calculate the probability of success in a single attempt.
If Alice has n replicas, and each replica can make k attempts per second, then her probability of finding a solution in any given second is:
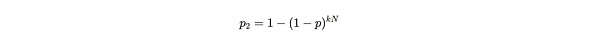
Formula Notes:kN means the total number of hash solution attempts Alice can make in one second, which is proportional to the number of unique copies Alice stores. For a specific explanation, please read the previous article "Arweave 2.6 may be more in line with Satoshi's vision". 1-p is the probability of a single attempt failing. The probability value of p2 is 1 minus the difference between the probability of kN attempts failing.
By substituting the above two formulas, we can get:
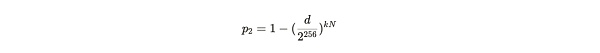
Formula Annotation:The result obtained by substituting p into the formula of P2
The time required for Alice to submit the proof can be simulated by a geometric random variable X ~ geom(p2), where p2 is the probability of success. This random variable X depends on d, k and n. In order to verify whether Alice is lying, Bob sends a difficulty d, so that Alice can submit a proof to Bob every 120 seconds on the premise that there are n copies. This is equivalent to Alice's success probability in 120 seconds:
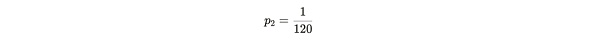
Formula Notes:1/120 is the probability of successfully submitting a proof within 120 seconds
If Alice can submit the proof within the required time, then she is likely to have the correct number of unique copies. But one proof is not enough to convince Bob that Alice is not lying. If Alice can submit the proof every 120 seconds on average for a long period of time, Bob can be reasonably sure that Alice has stored the expected amount of data.
Next, we try to quantify Bob's certainty about Alice's storage.
Suppose Alice claims to have stored 20 copies and consistently submitted proofs at an average speed of 120 seconds over 2 weeks (a total of 10,080 proofs submitted). At this point, Bob wonders what the probability is that Alice can still submit these proofs if she only stores 19 (or less) copies. This corresponds to the probability of providing proofs in different seconds:
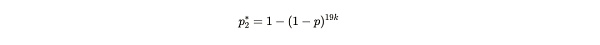
Formula Notes:The 19k that appears here means that Alice has stored 19 copies, and each copy has k attempts to find a solution.
Oversimplified:
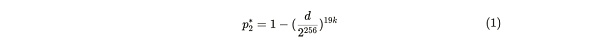
This probability can be calculated using the value of d generated by Bob for honest Alice. If she stores 19 or fewer copies, the probability that she can provide a proof in one second can be obtained by a series of derivations given below. Among them, p2 represents the probability of generating a proof within one second when Alice honestly stores 20 copies, and p2* represents the probability of providing a proof within one second if she is lying (storing ≤ 19 copies):
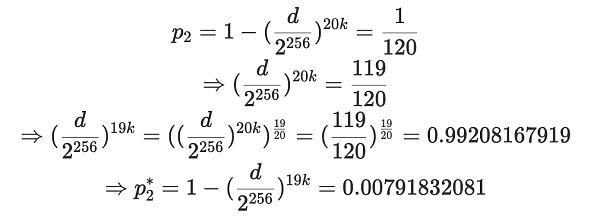
This derivation process seems very complicated, but in fact, friends with basic mathematical ability can understand it. The derivation process is the substitution process of the above company.
Therefore, p2*=0.00791832081, corresponding to the expected proof generation time of 126.2894 seconds. Let X* be the time for Alice to submit the proof obtained from p2*, that is, X*~ geom(p2*). This represents the expected value (average) of the time X* it takes Alice to submit a proof when she is lying and only stores 19 copies:
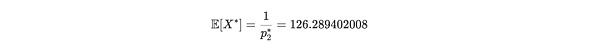
Formula Notes:E[X*] means that the average time it takes Alice to successfully submit a proof is 126.2894 seconds when she only stores 19 copies. If she stores 20 copies, the average time it takes to successfully submit a proof is 120 seconds.
We can use the central limit theorem to estimate the probability that the sample mean is less than 120, which is different from the expected value E[X*] obtained above. This probability is expressed as:
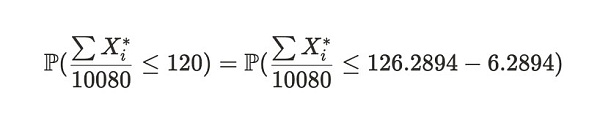
Formula Notes:The expression on the left side of the equation represents the probability that Alice's average time to submit a proof is less than or equal to 120 seconds within two weeks. The right side of the equation is a variant of the expression on the left.
For a large number of samples, the left side of this inequality tends to a normal distribution with mean E[X*] and variance σX*^2/n, where σX* is the standard deviation of Xd and n (here =10,080) is the sample size. We can transform this distribution into standard normal form to obtain the equivalent probability:Finally, using the standard normal distribution table, we can obtain the probability that Alice is lying in this week's time period:Therefore, in this example, Bob can judge with about 99.99997416% certainty that in this 2 Alice stores more than 19 copies of the dataset over the course of the week. We note that if Alice stores fewer than 19 copies, the expected proof submission time is greater than 126.3 seconds. We also note that the entire proof system only requires transmitting a proof once every 120 seconds. This is an average data transfer rate of 2.389 KB per second (280 KB/120 seconds) between Alice and Bob, which is comparable to the synchronization overhead of the Bitcoin network.
Finally, these probabilities do not change with arbitrary increases in the size of the dataset, and increasing the sampling period will continue to improve the accuracy of Bob's certainty about the number of Alice's copies at a superlinear rate (Figure 1).
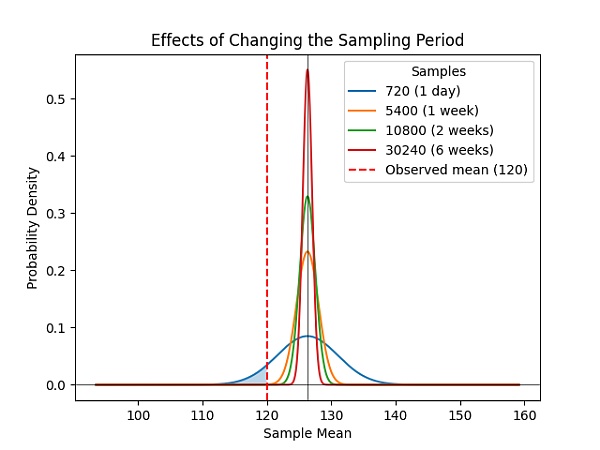
Figure 1: In Succinct Proof of Replication (SPoRes) games, determinism increases superlinearly with respect to sample duration. After two weeks of sample collection, the probability of maintaining less than 19 replicas is negligible (P<0.0000002584).
So, an SPoRes game is defined by the following parameters:
Where:
r = the Merkle root of the dataset used for the game.
k = the maximum number of challenges unlocked per replica per second.
d= The difficulty parameter that determines the success probability of each attempt.
Through these interesting mathematical derivations, we can rest assured that as long as miners continue to submit proofs within a reasonable period of time, we can determine whether the data is stored. This constitutes the core of Arweave's consensus mechanism aimed at decentralized storage. The fun of mathematics has just begun, and there will be more interesting deductions and demonstrations in the following articles.
Reference Links
1. Arweave Eco Twitter:
https://twitter.com/@ArweaveEco
2. #SPoA:
https://twitter.com/search?q=%23SPoA&src=hashtag_click
3. #SPoRes:
![]()
 JinseFinance
JinseFinance
 JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance JinseFinance
JinseFinance Others
Others Cointelegraph
Cointelegraph