Tác giả: Quantodian Nguồn: Medium Dịch: Shan Oppa, Golden Finance

Giới thiệu

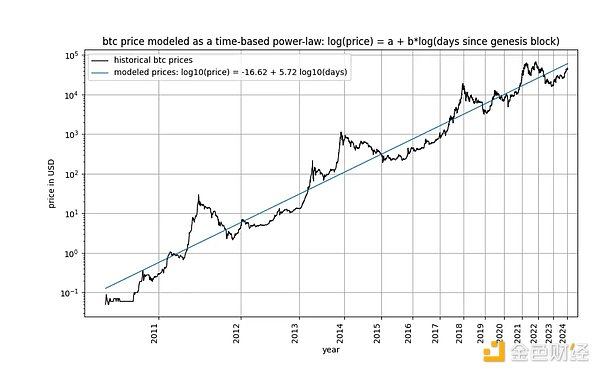
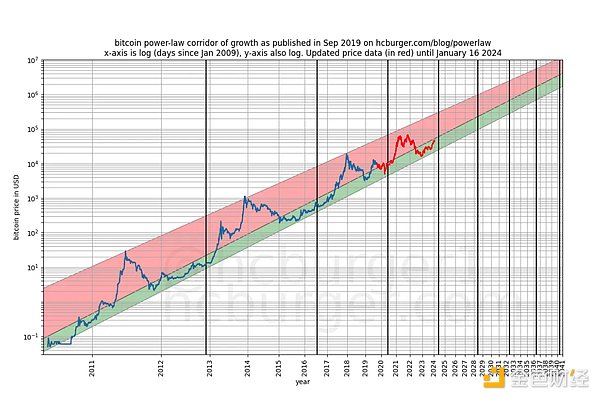
Luật sức mạnh dựa trên thời gian của Bitcoin được đề xuất lần đầu tiên bởi Giovanni Santostasi vào đầu năm 2014 và vào năm 2019 Re- được chúng tôi thể hiện (dưới dạng hành lang hoặc dưới dạng mô hình ba tham số), mối quan hệ giữa giá Bitcoin và thời gian được mô tả. Cụ thể, mô hình mô tả mối quan hệ tuyến tính giữa logarit số ngày kể từ khối khởi tạo của Bitcoin và logarit giá USD của Bitcoin.

p>

Mô hình này đã thu hút một số nhà phê bình, bao gồm Marcel Burger, Tim Stolte và Nick Emblow, những người từng viết "bác bỏ" cho mô hình. Trong bài viết này, chúng tôi muốn mổ xẻ một trong những lập luận chính trong ba lời chỉ trích này: cáo buộc thiếu sự đồng liên kết giữa thời gian và giá cả, khiến mô hình này bị coi là “không hợp lệ” và chỉ đơn thuần chỉ ra một mối quan hệ giả mạo.

Có thực sự như vậy không?

Trong bài viết này, chúng tôi sẽ xem xét kỹ lưỡng vấn đề này. Điều này dẫn chúng ta đến kết luận rằng, nói đúng ra, sự đồng liên kết không thể tồn tại trong các mô hình phụ thuộc vào thời gian, bao gồm cả mô hình của chúng ta. Tuy nhiên, không thể phủ nhận rằng một trong những tính chất thống kê cần thiết cho sự đồng liên kết tồn tại trong các mô hình luật lũy thừa dựa trên thời gian. Do đó, chúng tôi kết luận rằng các quy luật lũy thừa dựa trên thời gian được đồng liên kết theo nghĩa lỏng lẻo, rằng những người chỉ trích chúng tôi đã sai và mô hình đó hoàn toàn hợp lệ. Chúng tôi cho thấy rằng kết luận này có giá trị như nhau đối với mô hình stock-to-flow (S2F) và sự tăng trưởng theo cấp số nhân được quan sát thấy trong giá chỉ số thị trường chứng khoán dài hạn.

Giới thiệu về các khái niệm

Đồng tích hợp wtf

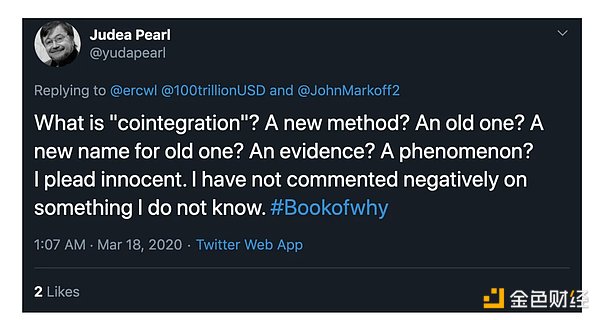
Bạn đã lạc đường rồi à? Có lẽ từ “đồng tích hợp” còn xa lạ với bạn? Đừng lo lắng: Judea Pearl, một chuyên gia về lý luận nhân quả và các mối quan hệ không giả tạo, đồng thời là tác giả cuốn Sách Tại sao, tuyên bố không biết gì về chủ đề này. Chúng tôi sẽ cố gắng làm rõ đầy đủ các thuật ngữ liên quan đến vấn đề hiện tại.

p>

Thú vị và hấp dẫn là cuộc tranh luận gay gắt về sự đồng tích hợp về X trong không gian #bitcoin, được đặc trưng bởi tính hời hợt rõ ràng của chủ đề. Nhiều người theo đuổi quy luật dòng chảy chứng khoán và quyền lực đang bối rối. Bạn đọc quan tâm có thể tự mình nhận thấy điều này bằng cách nhập cụm từ tìm kiếm “Đồng liên kết là gì” vào X. Trong khi một số người đóng góp dường như đã nắm vững và trau dồi hiểu biết của mình theo thời gian thì những người khác vẫn bối rối, đổi phe hoặc trở nên mất phương hướng. Chúng tôi chưa bao giờ thảo luận về chủ đề này cho đến bây giờ.

Một số thông tin cơ bản đầu tiên

Các quá trình ngẫu nhiên liên quan đến các biến ngẫu nhiên. Giá trị của biến ngẫu nhiên không được xác định trước. Ngược lại, một quá trình tất định có thể được dự đoán trước một cách chính xác—mọi khía cạnh của nó đều được biết trước. Những thứ như giá thị trường chứng khoán là ngẫu nhiên vì chúng ta không thể dự đoán trước giá của một tài sản. Do đó, chúng tôi coi chuỗi thời gian như giá cổ phiếu hoặc giá Bitcoin là quan sát các biến ngẫu nhiên.

Thay vào đó, thời gian trôi qua theo một khuôn mẫu xác định. Mỗi giây, mỗi khoảnh khắc trôi qua đều trôi qua - không có bất kỳ sự chắc chắn nào. Do đó, khoảng thời gian trôi qua sau khi một sự kiện xảy ra là một biến xác định.

Tính dừng của tín hiệu

Trước khi nghiên cứu về sự đồng liên kết, trước tiên chúng ta hãy xem xét đồng tích hợp Khái niệm cơ bản về tích hợp: ổn định:

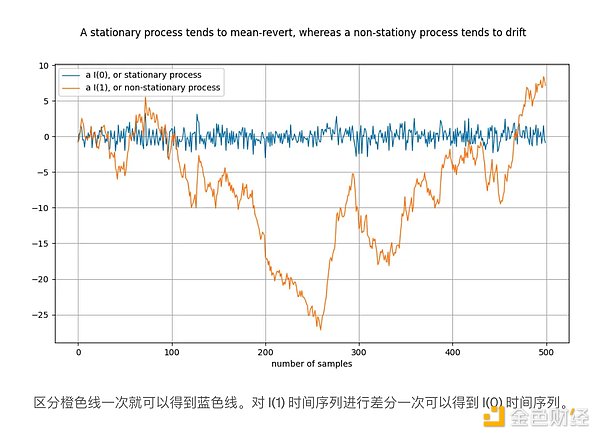
Quy trình đứng yên là một quá trình ngẫu nhiên, nói rộng ra, có cùng các đặc tính theo thời gian. Ví dụ về các đặc tính như vậy là giá trị trung bình và phương sai, được xác định và ổn định cho một quá trình đứng yên. Một từ đồng nghĩa với chuỗi thời gian dừng là I(0). Chuỗi thời gian từ các quá trình đứng yên không được "trôi dạt" và có xu hướng trở về giá trị trung bình, thường là bằng 0.

Một ví dụ về quá trình không cố định là bước đi ngẫu nhiên, mô tả chuyển động Brown hoặc sự khuếch tán hạt trong vật lý: mỗi giá trị mới trong bước đi ngẫu nhiên phụ thuộc vào Cộng một số ngẫu nhiên về giá trị trước đó. Các thuộc tính của một quá trình không cố định, chẳng hạn như giá trị trung bình và phương sai, thay đổi theo thời gian hoặc không được xác định. Các quy trình không cố định là I(1) hoặc cao hơn, nhưng thường là I(1). Chuỗi thời gian bắt nguồn từ các quá trình không cố định "trôi dạt" theo thời gian, nghĩa là có xu hướng di chuyển ra khỏi bất kỳ giá trị cố định nào.

Ký hiệu I(1) đề cập đến tần suất mà chuỗi thời gian cần phải được "vi phân" trước khi nó dừng lại. Sự khác biệt là sự khác biệt giữa một giá trị trong chuỗi thời gian và giá trị trước đó của nó. Điều này gần tương đương với việc lấy đạo hàm. Một chuỗi thời gian dừng đã là chuỗi dừng - nó cần sai số 0 lần để dừng, vì vậy nó là I(0). Chuỗi thời gian I(1) cần được vi phân một lần trước khi nó trở nên dừng.

Hình trên được xây dựng bằng cách thực hiện sai phân trên chuỗi thời gian màu cam để thu được chuỗi thời gian màu xanh lam. Tương tự, chuỗi thời gian màu cam thu được bằng cách lấy tích phân chuỗi thời gian màu xanh lam.

Quy trình nghiệm đơn vị ở đây đề cập đến một mô hình tự hồi quy (chính xác hơn là loại AR(1)) trong đó tham số rho được ước tính bằng 1 . Mặc dù chúng ta sử dụng rho và root thay thế cho nhau, rho đề cập đến các quá trình thường không được biết đến và cần được ước tính. Kết quả ước tính là giá trị "gốc".

Giá trị của rho thể hiện mức độ mà một tiến trình ghi nhớ các giá trị trước đó của nó. Giá trị của u đề cập đến hạng lỗi, được coi là nhiễu trắng.

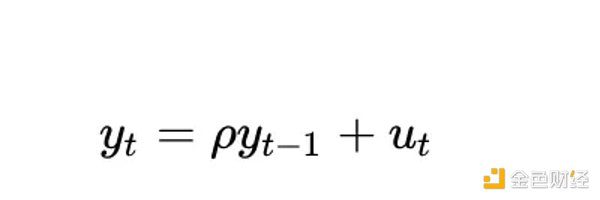p>

Quy trình gốc đơn vị là một bước đi ngẫu nhiên và không cố định. Các quy trình có giá trị "gốc" hoặc rho dưới 1 có xu hướng không bị trôi và do đó đứng yên. Về lâu dài, ngay cả các giá trị gần (nhưng thấp hơn) 1 cũng sẽ có xu hướng đảo chiều trung bình (chứ không phải trôi dạt). Do đó, một tiến trình gốc đơn vị là đặc biệt vì nó hoạt động khác về cơ bản với các tiến trình có gốc rất gần bằng 1. Hình bên dưới hiển thị 4 mẫu dữ liệu được tạo bởi 4 quy trình tự hồi quy đã biết, mỗi mẫu có giá trị rho khác nhau.

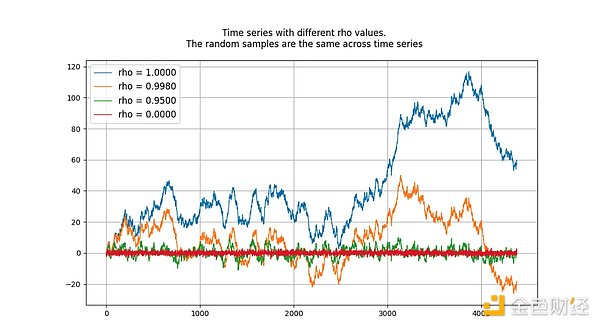p>

Sự đồng tích hợp của hai tín hiệu

Hai biến ngẫu nhiên (trong trường hợp của chúng tôi là thời gian Sự hiện diện hay vắng mặt đồng liên kết giữa các chuỗi). Để cặp được đồng liên kết, cả hai phải được tích hợp theo cùng một thứ tự và không cố định. Hơn nữa (và đây là phần quan trọng), phải tồn tại một tổ hợp tuyến tính cố định của hai chuỗi thời gian.

Ví dụ về không có tín hiệu đồng liên kết

Nếu hai chuỗi thời gian không cố định thì Các kết hợp tuyến tính (trong trường hợp đó chúng ta chỉ cần chọn sự khác biệt giữa hai chuỗi thời gian) cũng thường không cố định:

Ví dụ về tín hiệu đồng tích hợp

h2>< p style="text-align: left;">Nếu hai chuỗi thời gian không cố định trôi dạt "theo cùng một cách" trong thời gian dài, thì tổ hợp tuyến tính (ở đây chúng tôi chọn r2–0,5*r1) có thể đứng yên:< /p>

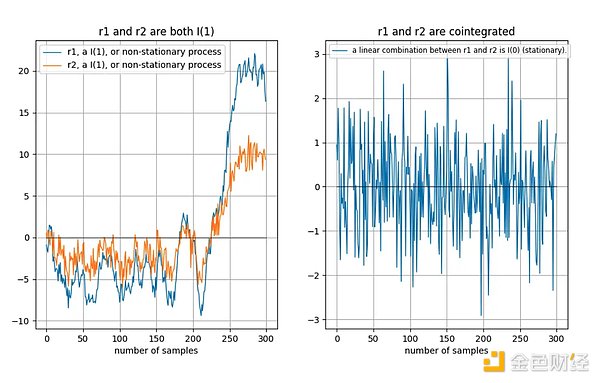
Tu và cộng sự [1] cung cấp một mô tả trực quan hay về sự đồng tích hợp:

"Sự tồn tại của mối quan hệ đồng liên kết giữa các chuỗi thời gian có nghĩa là chúng có sự trôi dạt ngẫu nhiên chung về lâu dài."

Tại sao lại hữu ích nếu hai chuỗi thời gian không dừng có tổ hợp tuyến tính dừng? Giả sử chúng ta có hai chuỗi thời gian x và y và chúng ta cố gắng lập mô hình y dựa trên x: y = a + b*x. Lỗi mô hình của chúng tôi được đưa ra bởi sự kết hợp tuyến tính của x và y: lỗi mô hình = y — a — b*x . Chúng tôi hy vọng rằng lỗi mô hình này ổn định, tức là nó không bị trôi về lâu dài. Nếu lỗi mô hình giảm dần trong thời gian dài, điều đó có nghĩa là mô hình của chúng tôi kém—không có khả năng đưa ra dự đoán chính xác.

Chi tiết xác định thành công hay thất bại

Có thể tìm thấy một định nghĩa chính thức hơn trong Engle và Granger's "Đồng liên kết" và sửa lỗi: Biểu diễn, ước tính và kiểm tra" [2] (Granger là người phát minh ra khái niệm đồng liên kết và nhận giải Nobel Kinh tế năm 2003), giải thưởng này xác định các khái niệm chính và các thử nghiệm để phát hiện đồng liên kết. Điểm mấu chốt của bài viết là giả định rằng chuỗi thời gian là ngẫu nhiên và không có thành phần xác định (chúng ta sẽ thảo luận vấn đề này sau).

p>

Áp dụng cho thời gian và giá Bitcoin

Trong trường hợp luật lũy thừa dựa trên thời gian , chúng tôi Có hai biến:

1. log_time: logarit của số ngày kể từ khối Genesis

2. log_price : logarit của giá

Theo định nghĩa của Engle và Granger, cả hai biến cần phải là biến ngẫu nhiên, không có thành phần xác định và không cần phải có tính cố định. Hơn nữa, chúng ta phải có khả năng tìm được tổ hợp tuyến tính dừng của hai biến. Ngược lại, không có sự đồng liên kết giữa hai biến.

Trước khi đi vào chi tiết, trước tiên chúng ta hãy hiển thị một số biểu đồ trên chính dữ liệu mô hình mà không có bất kỳ khái niệm nào về tính ổn định hoặc khái niệm đồng liên kết. Lưu ý rằng định luật lũy thừa dựa trên thời gian tạo ra sự phù hợp trông khá tốt về mặt trực quan. Vectơ dư không biểu thị ngay sự trôi dạt.

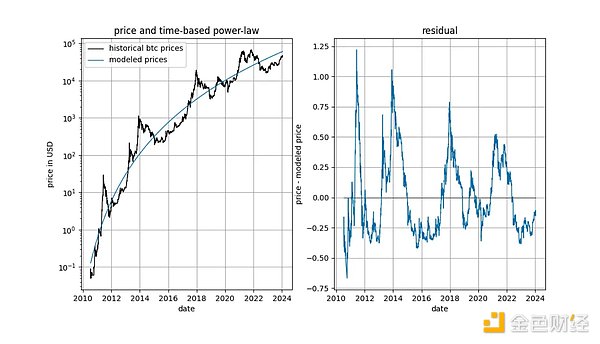p>

Hơn nữa, mô hình còn thể hiện hiệu suất ngoài mẫu xuất sắc (xem bên dưới). Hiệu suất ngoài mẫu xuất sắc không phù hợp với tuyên bố rằng mô hình là giả - một mô hình dựa trên các mối tương quan giả phải là: giả, nghĩa là nó không thể dự đoán chính xác. Hiệu suất ngoài mẫu có thể được kiểm tra bằng cách điều chỉnh mô hình với một lượng dữ liệu hạn chế (tối đa một ngày nhất định) và dự đoán khoảng thời gian khi mô hình không phù hợp (tương tự như xác thực chéo). Trong khoảng thời gian ngoài mẫu, giá được quan sát tiếp tục thường xuyên vượt qua giá được mô hình hóa và sự chênh lệch lớn nhất về giá được quan sát không di chuyển một cách có hệ thống khỏi giá được mô hình hóa.

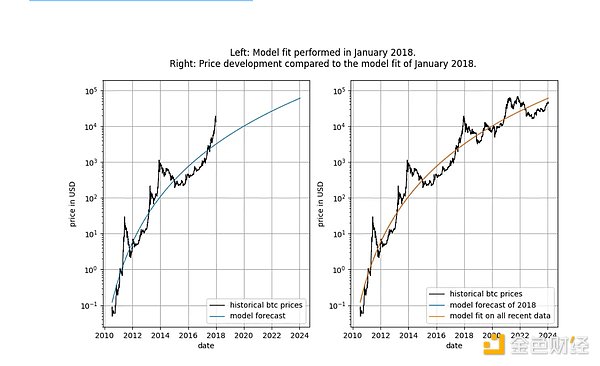p>

Chúng tôi có thể xem xét kỹ lưỡng hơn về hiệu suất của mô hình sau khi phát hành (tháng 9 năm 2019) vì chúng tôi không thể gian lận dưới bất kỳ hình thức nào sau khi mô hình được phát hành - chúng tôi không thể thay đổi nó sau khi thực tế Model.

p>

Bất kỳ cáo buộc nào cho rằng mô hình chỉ dựa trên các mối tương quan giả mạo đều phải được xem xét kỹ lưỡng về khả năng dự đoán của mô hình.

Đồng liên kết từng bước

Để có thể đồng liên kết giữa log_time và log_price , hai biến Mỗi phải là một tích phân biến ngẫu nhiên có cùng cấp và ít nhất phải là cấp 1.

biến log_price

log_price có phải là chuỗi thời gian đứng yên không? Nick kết luận rằng bằng cách sử dụng thử nghiệm ADF kiểu không xác định (kiểm tra không cố định) và thử nghiệm KPSS (kiểm tra tính dừng), log(price) chắc chắn là không cố định và do đó I(1) hoặc cao hơn. Marcel Burger kết luận bằng cách kiểm tra trực quan rằng I(1). Tim Stolte đã đưa ra một quan sát thú vị hơn: ông đã chạy thử nghiệm ADF trong các khoảng thời gian khác nhau (không xác định kiểu nào) và lưu ý rằng tình huống này không rõ ràng: "Vì vậy, chúng tôi không thể bác bỏ chắc chắn tính không cố định và kết luận rằng có một mức giá logarit." Dấu hiệu của sự không cố định."

Hãy tiến hành phân tích của riêng chúng ta. Tương tự như Tim Stolte, chúng tôi sẽ áp dụng thử nghiệm ADF vào các khoảng thời gian khác nhau: luôn bắt đầu từ ngày có sẵn đầu tiên và thêm một ngày mỗi ngày (chúng tôi sử dụng dữ liệu hàng ngày). Bằng cách này, chúng ta có thể thấy kết quả của bài kiểm tra ADF thay đổi như thế nào theo thời gian. Nhưng không giống như Tim và Nick, chúng tôi sẽ chỉ định phiên bản thử nghiệm ADF nào sẽ chạy. Theo Wikipedia, các thử nghiệm DF và ADF có ba loại chính:

Sự khác biệt giữa ba phiên bản này là khả năng đáp ứng (loại bỏ) các xu hướng khác nhau. Điều này liên quan đến yêu cầu của Engle và Granger về việc loại bỏ bất kỳ xu hướng xác định nào - ba phiên bản này có thể loại bỏ ba loại xu hướng xác định đơn giản. Phiên bản đầu tiên cố gắng mô tả các thay đổi log_price hàng ngày chỉ bằng cách sử dụng dữ liệu log_price trong quá khứ. Phiên bản thứ hai cho phép sử dụng thuật ngữ không đổi, với hiệu ứng là log_price có thể có xu hướng tuyến tính (lên hoặc xuống). Phiên bản thứ ba cho phép các thành phần bậc hai (parabol).

Chúng tôi không biết Tim và Nick đang chạy phiên bản nào nhưng chúng tôi sẽ chạy cả ba phiên bản.

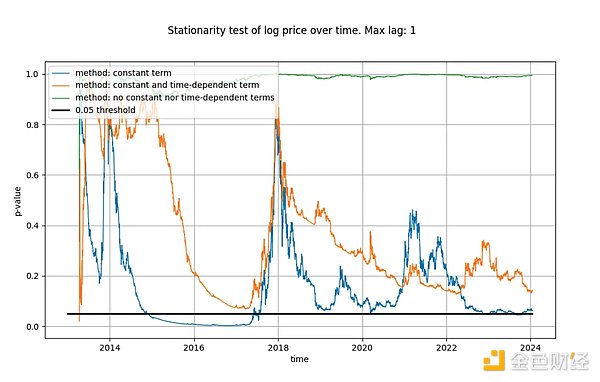
Độ trễ tối đa mà chúng tôi sử dụng trong thử nghiệm ADF là 1, nhưng việc sử dụng độ trễ dài hơn không làm thay đổi đáng kể kết quả và kết luận của chúng tôi. Chúng tôi sẽ sử dụng hàm statsmodels.tsa.stattools.adfuller của python, trong đó "maxlag" là 1 và sẽ sử dụng tham số "n", "c" và "ct" làm tham số "hồi quy" (tương đương với ba tham số được mô tả bởi Wikipedia kiểu trên) ). Trong hình bên dưới, chúng tôi hiển thị giá trị p (thước đo có ý nghĩa thống kê) được thử nghiệm trả về, trong đó giá trị thấp hơn có nghĩa là khả năng dừng cao hơn (thường sử dụng ngưỡng 0,05).

p>

Chúng tôi nhận thấy rằng kiểu đầu tiên (đường màu xanh lá cây) kết luận rõ ràng rằng chuỗi thời gian log_price là không cố định. Phiên bản thử nghiệm thứ ba (đường màu cam) dẫn đến kết luận tương tự nhưng ít mang tính quyết định hơn. Điều thú vị là, phép kiểm tra xem xét một số hạng không đổi (đường màu xanh) không thể xác định liệu chuỗi thời gian có dừng hay không (Tim rất có thể cũng đã sử dụng phép kiểm tra ADF với số hạng không đổi). Tại sao ba phiên bản này lại khác nhau và đặc biệt là tại sao phiên bản có số hạng không đổi không loại trừ log_price khỏi trạng thái đứng yên?

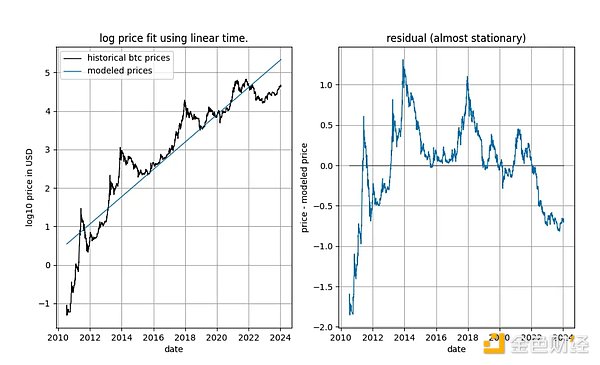
Chỉ có thể có một cách giải thích: chỉ sử dụng một số hạng không đổi trong chênh lệch log_price (dẫn đến một số hạng tuyến tính trong log_price) phù hợp với chuỗi thời gian "tốt", Điều này dẫn đến tín hiệu dư xuất hiện gần như đứng yên (mặc dù có độ lệch đáng kể ở đầu và cuối). Cho đến nay, việc không sử dụng xu hướng xác định nào trong log_price hoặc sử dụng hiệu ứng xác định bậc hai đã hoạt động kém.

p>

Điều này đã cho chúng ta một gợi ý rõ ràng rằng có mối quan hệ giữa thời gian và log_price. Trên thực tế, nếu kiểm tra ADF sử dụng số hạng không đổi kết luận rằng tín hiệu là dừng, điều này có nghĩa là số hạng thời gian tuyến tính có thể xấp xỉ log_price đủ tốt để thu được số dư ổn định. Việc thu được phần dư dừng là điều mong muốn vì đó là dấu hiệu của một mối quan hệ không giả mạo (tức là chúng ta đã tìm thấy các biến giải thích chính xác). Xu hướng thời gian tuyến tính không hoàn toàn là thứ chúng ta cần, nhưng có vẻ như chúng ta đã khá gần nhau.

Kết luận của chúng tôi khác biệt đáng kể so với kết luận của Marcel Berg, người đã tuyên bố (trong một bài viết khác):

"Trong phân tích trước đây, tôi đã chỉ ra rằng giá của Bitcoin là không thể thiếu đối với đơn đặt hàng đầu tiên, và nó vẫn như vậy. Bitcoin là Sự phát triển của giá theo thời gian không thể hiện bất kỳ yếu tố xác định nào."

Chúng tôi kết luận rằng thời gian tuyến tính không giải thích đầy đủ hành động giá của Bitcoin theo thời gian, nhưng hoàn toàn rõ ràng rằng log_price có yếu tố thời gian xác định. Hơn nữa, không rõ liệu log_price có phải là I(1) hay không sau khi loại bỏ các thành phần xác định thích hợp (theo yêu cầu của Engel và Granger). Thay vào đó, nó dường như không có xu hướng ổn định, nhưng vẫn cần phải tìm ra thành phần xác định thích hợp.

Nếu chúng ta đang tìm kiếm sự đồng liên kết, thì việc log_price không phải là I(1) đã là một vấn đề rồi, bởi vì để hai biến được đồng liên kết thì chúng phải Tất cả là tôi (1) hoặc cao hơn.

biến log_time

Bây giờ chúng ta hãy xem biến log_time. Marcel Burger kết luận rằng log_time dường như là tích phân bậc sáu (ông giữ nguyên hiệu cho đến khi gặp vấn đề về số). Cách ông mong đợi một hàm toán học như logarit biến đổi từ một biến hoàn toàn xác định thành một biến ngẫu nhiên là vô lý.

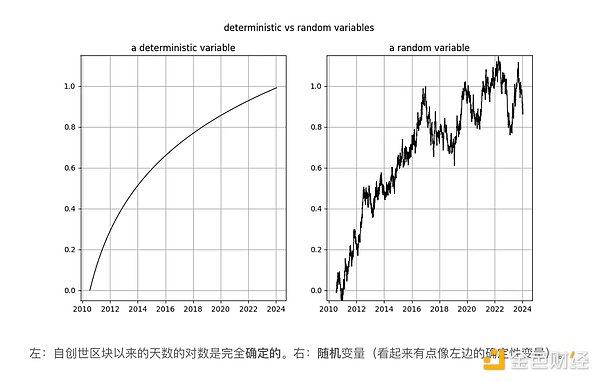
Nick đi đến kết luận tương tự đối với các biến log_time và log_price: nó chắc chắn là không cố định và do đó I(1) hoặc cao hơn. Tim Stolte tuyên bố rằng log_time không cố định khi xây dựng. Đây là những tuyên bố đáng ngạc nhiên! Trật tự tích phân và đồng liên kết đề cập đến khái niệm các biến ngẫu nhiên và loại bỏ mọi xu hướng xác định khỏi chúng (xem Engle và Granger [2] ở trên). Xin nhắc lại: giá trị của các biến xác định được biết trước, trong khi giá trị của các biến ngẫu nhiên thì không. Thời gian (rõ ràng) hoàn toàn mang tính xác định, và hàm logarit cũng vậy, do đó log_time cũng hoàn toàn mang tính xác định.

p>

Nếu chúng ta làm theo Engle và Granger và loại bỏ xu hướng tất định khỏi log_time, chúng ta sẽ còn lại một vectơ các số 0 vì log(x) — log( x) = 0, tức là chúng ta vẫn có tín hiệu hoàn toàn xác định. Điều này có nghĩa là chúng tôi bị mắc kẹt - chúng tôi không thể chuyển biến log_time hoàn toàn xác định thành biến ngẫu nhiên, vì vậy chúng tôi không thể sử dụng khung của Engle và Granger.

Một cách khác để hiểu mức độ có vấn đề của một biến hoàn toàn xác định trong phân tích đồng liên kết là xem xét cách các phép kiểm tra tính dừng (chẳng hạn như phép kiểm tra Dickey-Fuller) xử lý nó. Chúng ta hãy xem xét trường hợp đơn giản nhất (trong đó y là biến quan tâm, rho là hệ số được ước tính và u là thuật ngữ lỗi được coi là nhiễu trắng):

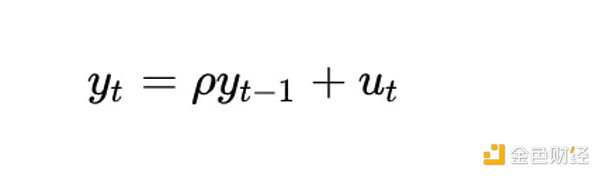
Lẽ ra chuyện gì đã xảy ra? Thuật ngữ lỗi u_{t} là 0 cho tất cả các giá trị của t vì chúng tôi không có thành phần ngẫu nhiên - không cần có lỗi. Nhưng vì log_time là hàm phi tuyến của thời gian nên giá trị của rho cũng phải phụ thuộc vào thời gian.

Đối với các biến ngẫu nhiên, mô hình này hữu ích hơn vì biến rho nắm bắt được mức độ bộ nhớ của các giá trị ngẫu nhiên trước đó. Nhưng không có giá trị ngẫu nhiên, mô hình sẽ vô nghĩa.

Các loại thử nghiệm khác cũng gặp phải vấn đề tương tự như các biến xác định.

Do đó, các biến xác định hoàn toàn không thuộc phân tích đồng liên kết. Hay nói cách khác: phân tích đồng liên kết không hoạt động với các tín hiệu xác định và nếu một trong các tín hiệu có tính xác định thì phân tích đồng liên kết là một công cụ lỗi thời để khẳng định các mối quan hệ giả.

Tôi nên làm gì?

Sự đồng liên kết chỉ được xác định giữa hai biến đều là I(d), trong đó d ít nhất bằng 1. Chúng tôi đã chỉ ra rằng log_time là một biến hoàn toàn xác định và không thể được sử dụng trong các thử nghiệm về tính dừng. Chúng ta không thể nói log_time là I(0), I(1) hay I(6). Ngoài ra, log_price không phải là I(1) mà có xu hướng dừng.

Có phải thực tế là không có sự đồng liên kết xác định giữa log_time và log_price có nghĩa là các quy luật lũy thừa dựa trên thời gian là không hợp lệ hoặc giả mạo về mặt thống kê?

Việc sử dụng kết hợp các biến xác định và xu hướng dừng trong bất kỳ phân tích thống kê thích hợp nào là hoàn toàn hợp lệ. Như các nhà phê bình của chúng tôi muốn tin tưởng, sự đồng liên kết không phải là điểm trung tâm trong việc phân tích các mối quan hệ thống kê.

Vì vậy, việc đồng liên kết là không thể. Nhưng phân tích tính dừng có thể vẫn có chỗ đứng khi áp dụng cho các mô hình luật lũy thừa. Hãy khám phá điều này hơn nữa.

Lý do tại sao lần đầu tiên chúng tôi tiến hành phân tích đồng liên kết giữa các biến đầu vào là vì chúng tôi hy vọng tìm thấy sự kết hợp tuyến tính cố định của cả hai. Không có lý do cơ bản nào giải thích tại sao không thể kết hợp một biến xác định (log_time) và một biến cố định theo xu hướng (log_price) để thu được một biến cố định. Do đó, thay vì tìm kiếm sự đồng liên kết theo nghĩa chặt chẽ (vì phần dư chỉ là sự kết hợp tuyến tính của hai tín hiệu đầu vào), chúng ta có thể chỉ cần thực hiện kiểm tra tính dừng trên phần dư. Nếu phần dư là dừng, chúng ta sẽ tìm thấy các tổ hợp tuyến tính dừng (là mục tiêu của quá trình đồng liên kết) ngay cả khi chúng ta không tuân thủ nghiêm ngặt phép thử đồng liên kết Engel-Granger.

Nghiên cứu sâu hơn

James G. MacKinnon trong bài viết "Kiểm tra hợp nhất Điều này được giải thích chính xác trong "Giá trị tới hạn của"[3]: Kiểm tra đồng liên kết (kiểm tra Engle Granger) giống như kiểm tra tính ổn định của phần dư (kiểm tra DF hoặc ADF). Nếu hồi quy "đồng liên kết"" (thay thế log_time Hồi quy được liên kết với log_price) đã được thực hiện:

MacKinnon lặp lại tuyên bố này: Nếu các tham số kết nối log_time và log_price đã biết trước, thì bạn có thể bỏ qua quá trình đồng tích hợp Engle Granger thay vào đó thực hiện một trong ba kiểu kiểm tra tính dừng phổ biến (kiểm tra DF hoặc ADF) trên phần dư:

Do đó, chúng ta có thể sử dụng một trong hai phương pháp, trong đó giống hệt nhau ngoại trừ thống kê kiểm tra được tạo:

1. Khớp log_time với log_price và tính toán số dư ( lỗi). Dựa trên phần dư này, hãy tính toán thử nghiệm DF hoặc ADF tốt hơn. Thống kê kết quả cho chúng ta biết liệu phần dư có Tĩnh tại hay không.

2. Giả sử log_time và log_price là I(1) và chạy thử nghiệm đồng liên kết Engle-Granger. Số liệu thống kê thu được cũng cho chúng ta biết liệu phần dư có đứng yên hay không.

Đối với kiểm tra ADF, hãy sử dụng hàm statsmodels.tsa.stattools.adfuller của python; đối với kiểm tra Engle-Granger, chúng tôi sử dụng mô hình thống kê .tsa.stattools.coint. Đối với cả hai hàm, chúng tôi sử dụng hương vị không sử dụng hằng số (không có độ lệch liên tục theo thời gian) vì phần dư của chúng tôi không được chứa độ lệch liên tục theo thời gian (vì điều này có nghĩa là theo thời gian, mô hình bắt đầu vượt quá hoặc dưới giá ).

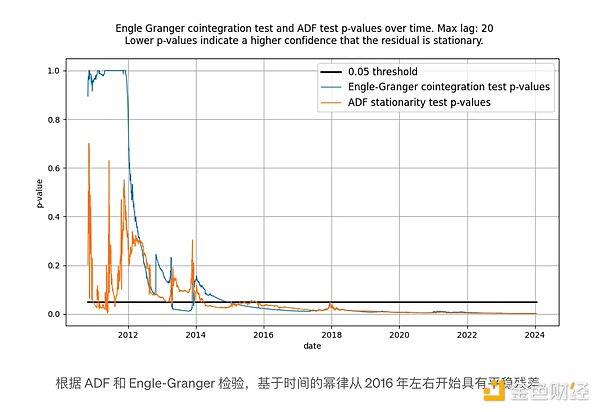
Chúng tôi đã viết rằng các bài kiểm tra ADF và Engle-Granger là tương đương nhau, nhưng điều này không hoàn toàn đúng: chúng không đưa ra số liệu thống kê kiểm tra giống nhau. Thử nghiệm đồng liên kết Engle-Granger giả định N=2 biến ngẫu nhiên, trong khi thử nghiệm ADF giả định N=1 biến ngẫu nhiên (N là thước đo mức độ tự do). Một biến ngẫu nhiên có thể bị ảnh hưởng bởi một biến ngẫu nhiên khác hoặc một biến xác định, nhưng một biến xác định không thể bị ảnh hưởng bởi một biến ngẫu nhiên. Do đó, trong trường hợp của chúng tôi (chỉ với một biến xác định log_time), số liệu thống kê được trả về bởi thử nghiệm ADF (giả sử N=1 biến ngẫu nhiên) được ưu tiên. Về nguyên tắc, các thử nghiệm Engle-Granger và ADF có thể không nhất quán, nhưng trên thực tế, điều này không xảy ra đối với các mô hình dựa trên thời gian. Như thể hiện trong hình bên dưới, kết luận vẫn như nhau: chúng ta thu được một vectơ dư cố định.

p>

Ban đầu cả hai phép thử đều không cho thấy phần dư cố định, điều này là bình thường. Điều này là do có các thành phần tần số thấp trong tín hiệu dư, có thể bị nhầm lẫn với tín hiệu không cố định. Chỉ theo thời gian, giá trị trung bình còn lại mới phục hồi đáng kể và trở nên ổn định một cách hiệu quả.

S2F và giá chỉ số chứng khoán dài hạn

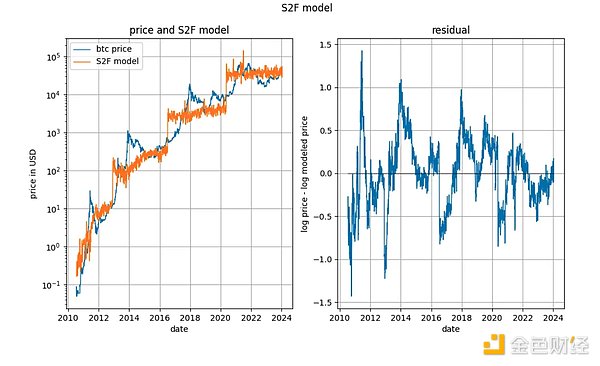
Mô hình S2F dường như đã được áp dụng rộng rãi bị bỏ qua vì việc đồng liên kết chặt chẽ hóa ra là không thể vì một lý do tương tự như lý do của các định luật lũy thừa dựa trên thời gian: các biến đầu vào xác định (một phần). Tuy nhiên, phần dư do mô hình tạo ra có vẻ rất ổn định.

p>

Trên thực tế, cả phép thử đồng liên kết Engle-Granger và phép kiểm tra tính dừng của ADF (được ưu tiên vì có một biến xác định và một biến ngẫu nhiên) đều mang lại p rất gần với giá trị 0. Do đó, không nên loại trừ cơ sở cho việc mô hình S2F "thiếu đồng liên kết" (thực ra có nghĩa là "thiếu tính ổn định").

Tuy nhiên, chúng tôi đã chỉ ra vào đầu năm 2020 rằng có những dấu hiệu khác cho thấy mô hình S2F không nên giữ vững. Dự đoán của chúng tôi rằng giá BTCUSD sẽ thấp hơn dự đoán của mô hình S2F đã được chứng minh là đúng đắn.

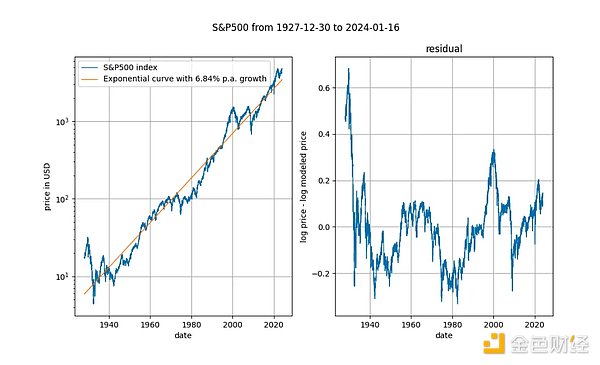
Thật thú vị khi xem xét các chỉ số giá cổ phiếu dài hạn theo thời gian (đây là S&P 500 không có cổ tức tái đầu tư). Được biết, các chỉ số thị trường chứng khoán lớn đều tăng trưởng với tốc độ chỉ số trung bình khoảng 7%. Trên thực tế, chúng tôi xác nhận điều này bằng hồi quy hàm mũ.

p>

Ở đây một lần nữa chúng ta có một biến xác định (thời gian). Thử nghiệm đồng liên kết Engle Granger mang lại giá trị p xấp xỉ 0,025 và thử nghiệm ADF (ưu tiên) mang lại giá trị p xấp xỉ 0,0075 (nhưng các giá trị này phụ thuộc nhiều vào khoảng thời gian chính xác đã chọn). Một lần nữa, phần dư cố định. Xu hướng thời gian hàm mũ trong giá cổ phiếu là hợp lệ.

Tác động

Mô hình S2F ban đầu được phát triển nhờ nền tảng kinh tế lượng tốt (đặc biệt là liên kết (đặc biệt là Marcel Burger và Nick Emblow). Khi tình thế thay đổi và người ta phát hiện ra rằng mô hình S2F không thể tồn tại để đồng liên kết (theo nghĩa chặt chẽ), cả Marcel và Nick đều từ bỏ và tuyên bố mô hình S2F không hợp lệ. Có vẻ như sau sự việc này, quan điểm của người dân về mô hình S2F cũng đã thay đổi. Eric Wall có một bản tóm tắt ngắn rất hay về diễn biến của các sự kiện.

Chúng tôi đã giải thích và tài liệu kinh tế lượng (MacKinnon [3]) đồng ý với chúng tôi rằng đồng liên kết và ổn định gần như có thể sử dụng thay thế cho nhau (ngoại trừ các giá trị thống kê). Sử dụng cái nhìn sâu sắc này, chúng tôi thấy rằng mô hình S2F không có bất kỳ vấn đề nào với tính đồng liên kết/dừng lại, vì vậy sẽ là sai lầm nếu thay đổi suy nghĩ của một người về mô hình S2F vì giả định thiếu sự đồng liên kết. Chúng tôi đồng ý rằng mô hình S2F sai, nhưng nó sai vì những lý do khác ngoài việc thiếu sự đồng liên kết.

Luật lũy thừa dựa trên thời gian của Bitcoin đã bị chỉ trích vì thiếu sự đồng liên kết, bị cáo buộc gắn nhãn mối quan hệ giữa log_time và log_price là giả mạo. Chúng tôi đã chỉ ra rằng quy luật lũy thừa dựa trên thời gian của Bitcoin rõ ràng có phần dư cố định, vì vậy lý luận của những người chỉ trích chúng tôi là vô nghĩa.

Mô hình luật lũy thừa dựa trên thời gian của Bitcoin rất hiệu quả, ổn định và mạnh mẽ. như mọi khi.